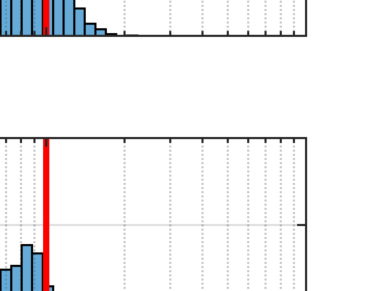
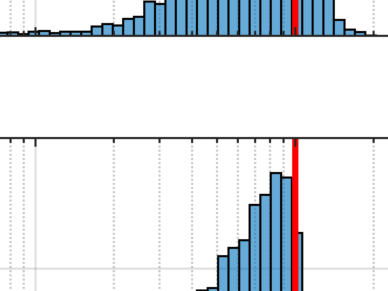
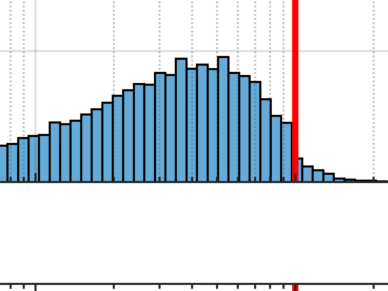
In this paper we consider regression problems subject to arbitrary noise in the operator or design matrix. This characterization appropriately models many physical phenomena with uncertainty in the regressors. Although the problem has been studied extensively for ordinary/total least squares, and via models that implicitly or explicitly assume Gaussianity, less attention has been paid to improving estimation for regression problems under general uncertainty in the design matrix. To address difficulties encountered when dealing with distributions of sums of random variables, we rely on the saddle point method to estimate densities and form an approximate log-likelihood to maximize. We show that the proposed method performs favorably against other classical methods.
翻译:在本文中,我们考虑在操作者或设计矩阵中出现任意噪音的回归问题,这种定性适当地模型了许多物理现象,在回归者中具有不确定性。虽然这个问题已经对普通/全部最小方块进行了广泛研究,并通过隐含或明确假定高斯的模型进行了广泛研究,但对于改进设计矩阵中一般不确定性情况下回归问题的估算,没有那么重视。为了解决在处理随机变量总量分配时遇到的困难,我们依靠支撑点方法来估计密度并形成一种大致的日志相似性以最大化。我们表明,拟议的方法与其他经典方法相比效果较好。