Gaussian Processes with Errors in Variables: Theory and Computation

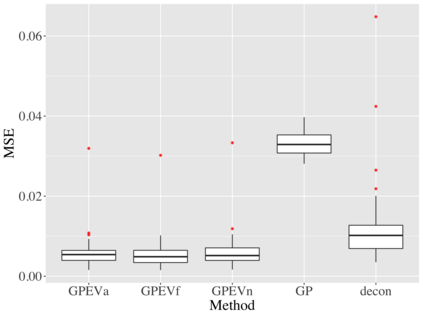
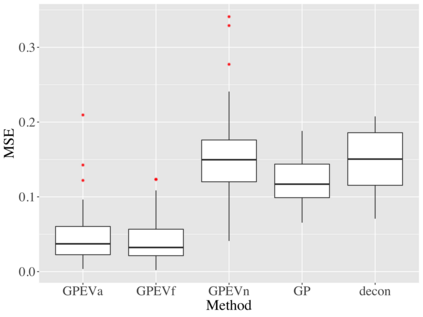
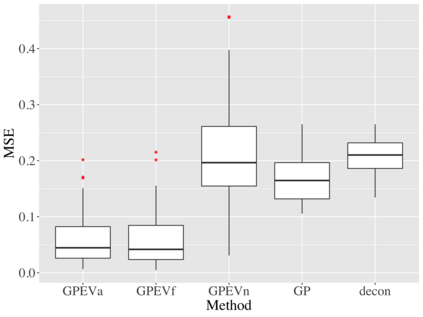
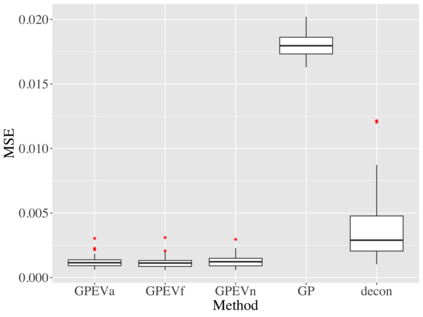
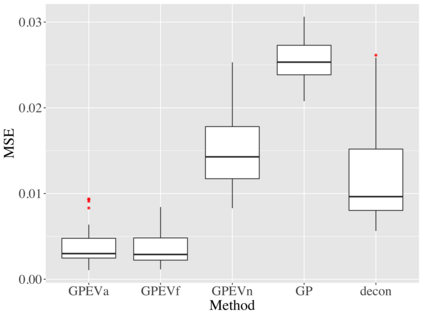
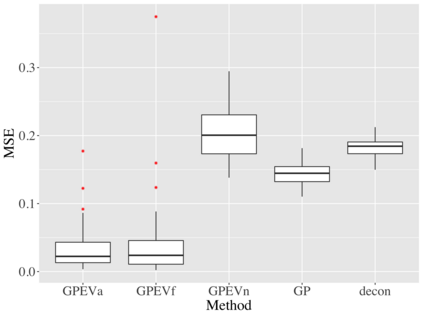
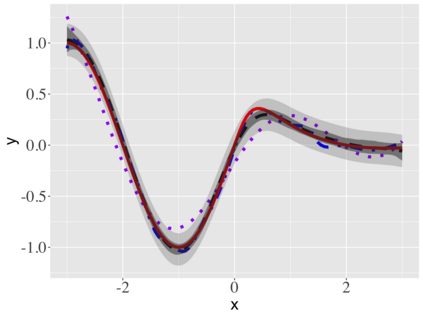
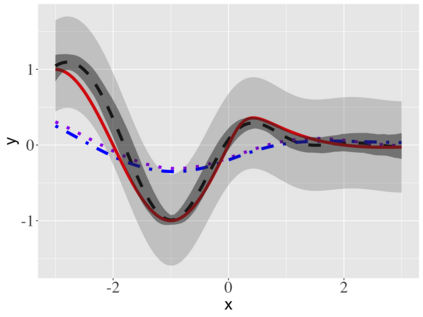
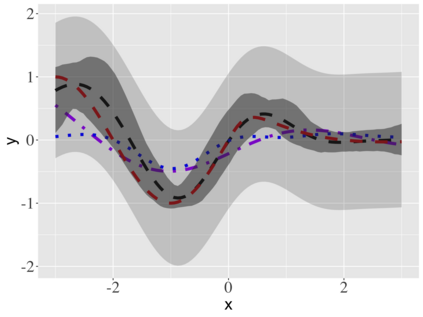
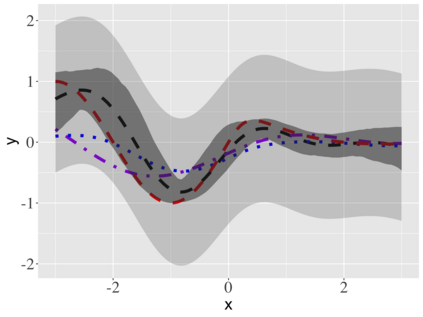
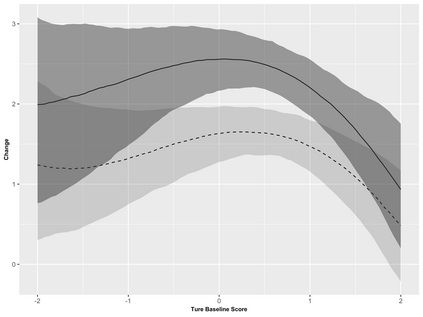
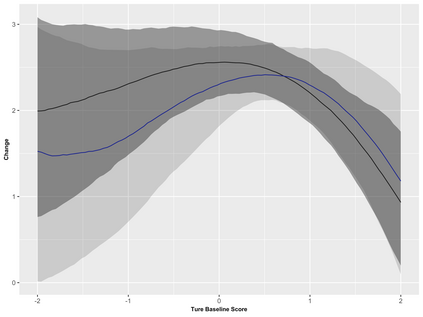
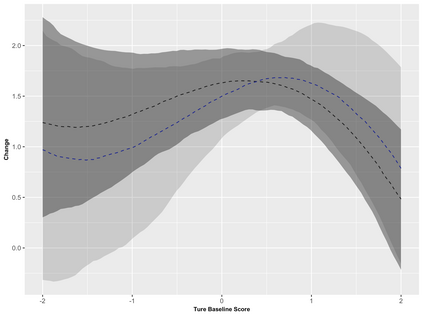
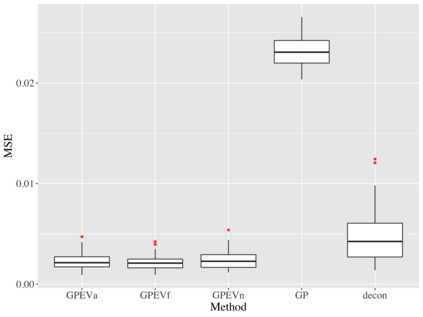
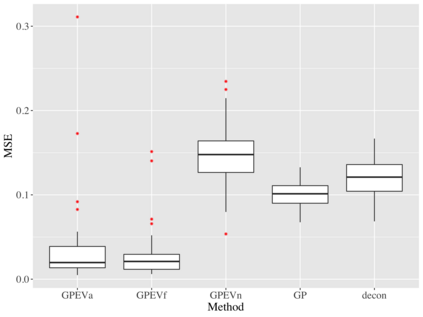
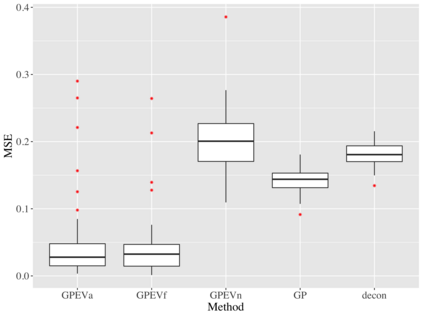
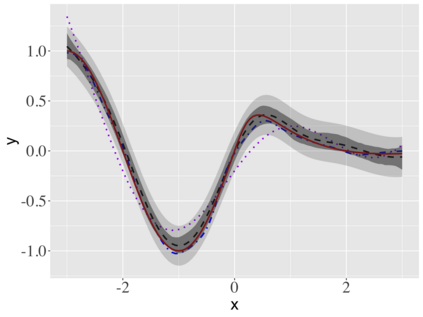
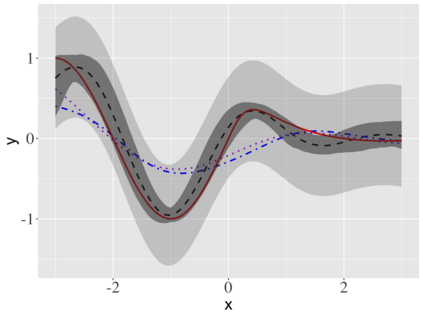
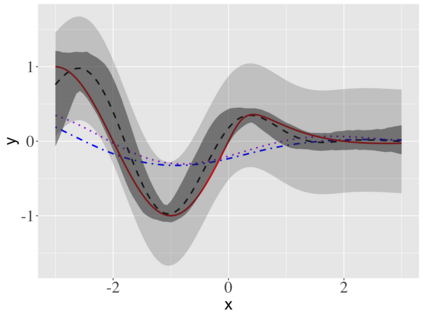
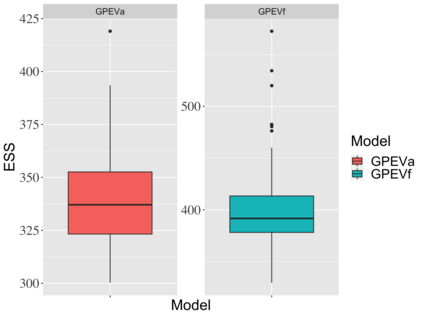
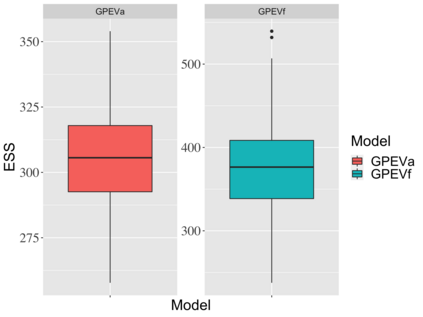
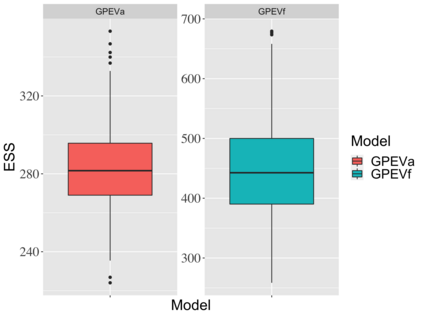
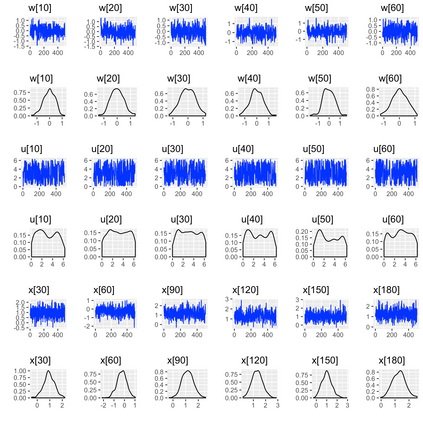
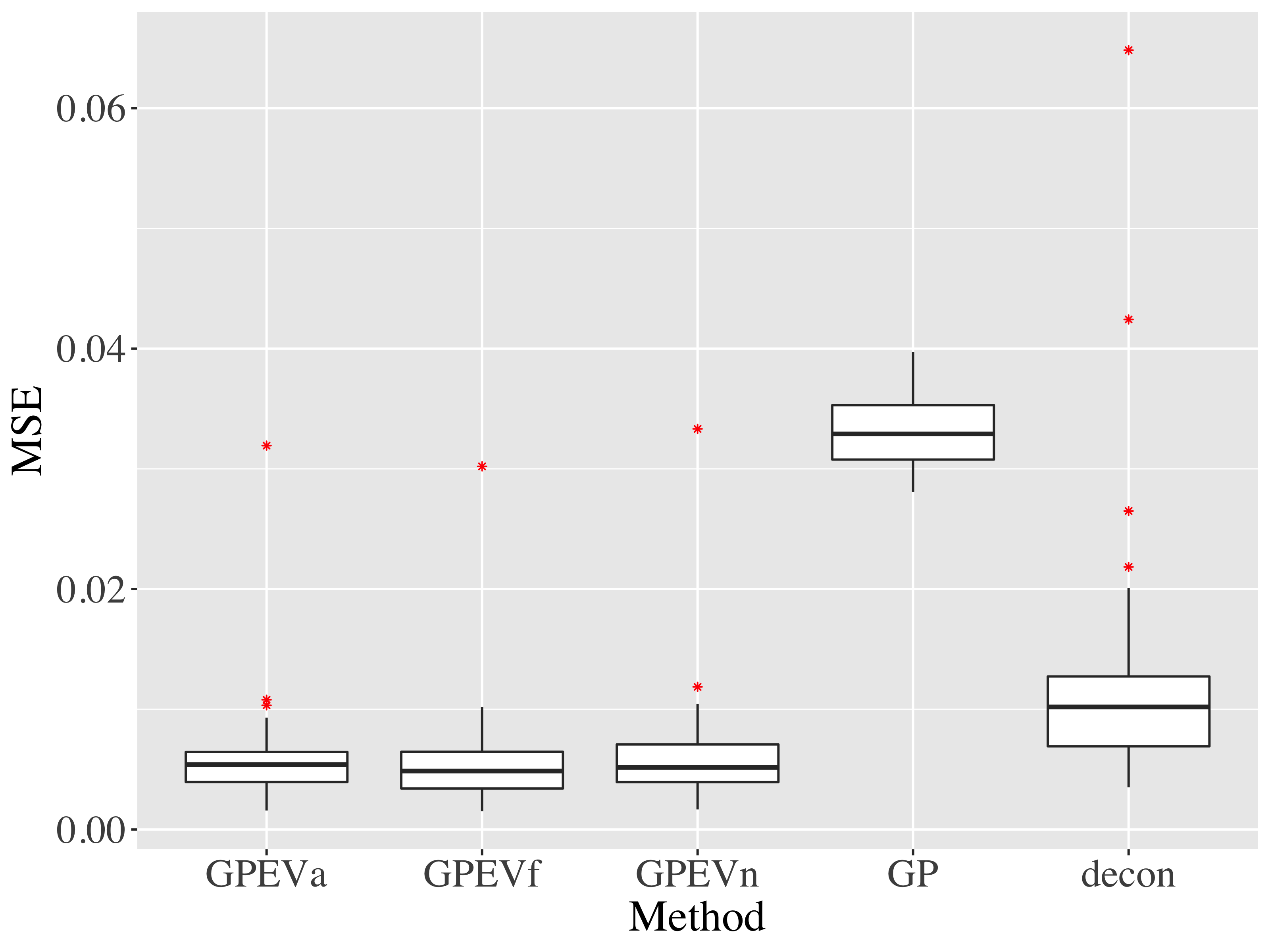
Covariate measurement error in nonparametric regression is a common problem in nutritional epidemiology and geostatistics, and other fields. Over the last two decades, this problem has received substantial attention in the frequentist literature. Bayesian approaches for handling measurement error have only been explored recently and are surprisingly successful, although the lack of a proper theoretical justification regarding the asymptotic performance of the estimators. By specifying a Gaussian process prior on the regression function and a Dirichlet process Gaussian mixture prior on the unknown distribution of the unobserved covariates, we show that the posterior distribution of the regression function and the unknown covariates density attain optimal rates of contraction adaptively over a range of H\"{o}lder classes, up to logarithmic terms. This improves upon the existing classical frequentist results which require knowledge of the smoothness of the underlying function to deliver optimal risk bounds. We also develop a novel surrogate prior for approximating the Gaussian process prior that leads to efficient computation and preserves the covariance structure, thereby facilitating easy prior elicitation. We demonstrate the empirical performance of our approach and compare it with competitors in a wide range of simulation experiments and a real data example.