Holistic Cube Analysis: A Query Framework for Data Insights

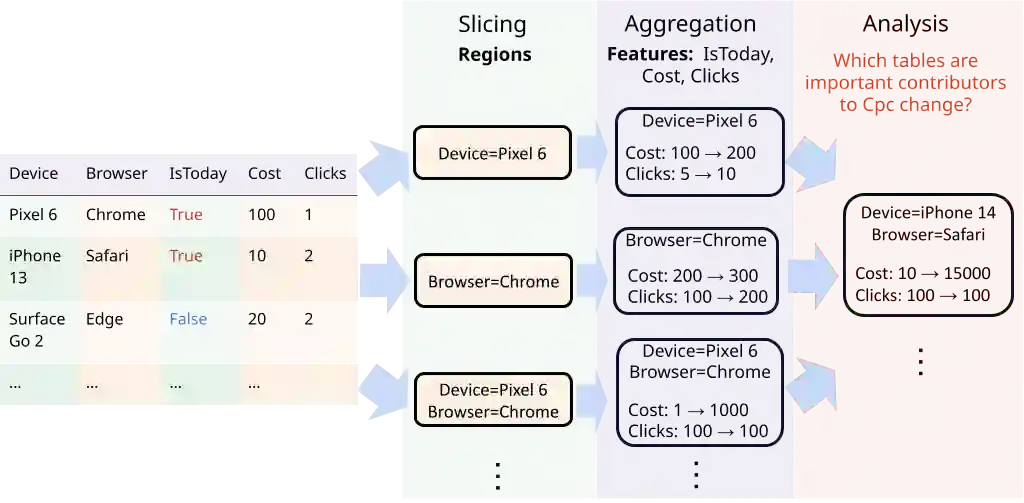
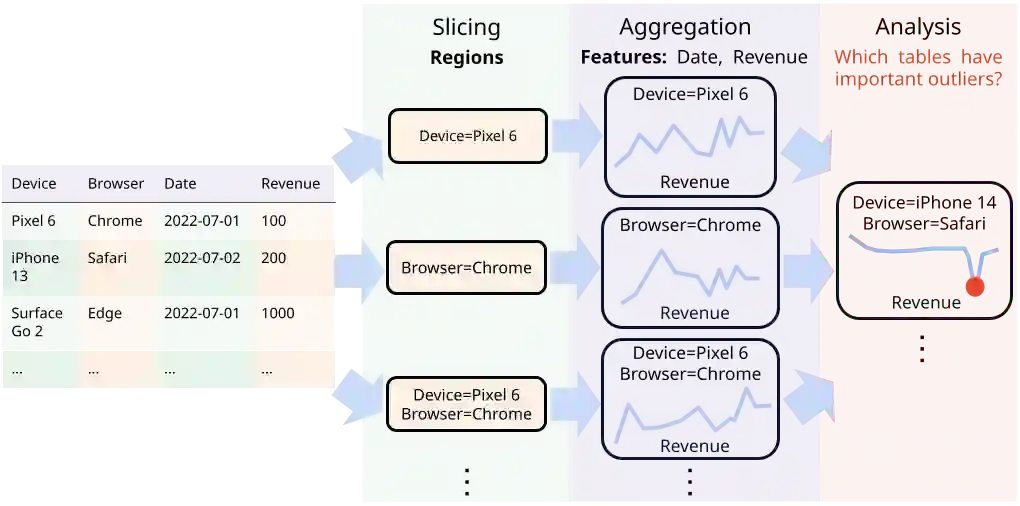
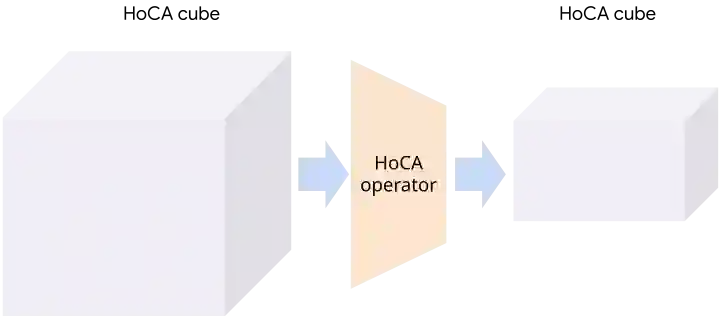
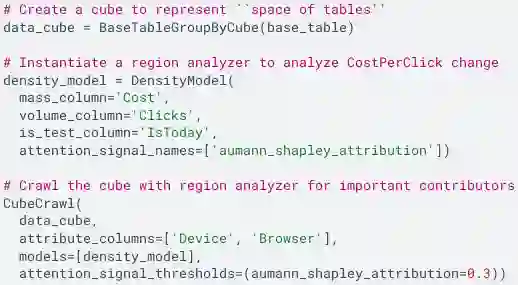
Many data insight questions can be viewed as searching in a large space of tables and finding important ones, where the notion of importance is defined in some adhoc user defined manner. This paper presents Holistic Cube Analysis (HoCA), a framework that augments the capabilities of relational queries for such problems. HoCA first augments the relational data model by defining a new data type AbstractCube, which is defined as a function from RegionFeatures space to relational tables. AbstractCube provides a logical form of data for HoCA programs, abstracting away their exact encoding. With this function-as-data modeling, HoCA operators are thus cube-to-cube transformations. We describe two basic but fundamental HoCA operators, cube crawling and cube join (with many possibilities to extend). Cube crawling explores a region space, and outputs a cube that maps regions to signal vectors. Cube join, in turn, is critical for composition, allowing one to join information from different cubes for deeper analysis. Cube crawling introduces two novel programming features, (programmable) Region Analysis Models (RAMs) and Multi-Model Crawling. Crucially, RAM has a notion of population features, which allows one to go beyond only analyzing local features at a region, and program region-population analysis that compares region and population features, capturing a large class of importance notions in data insights. HoCA poses a rich algorithmic space, and we describe several cube crawling implementations leveraging different foundations, and evaluate their performance. We have implemented and deployed HoCA at Google. Even in this early stage, our HoCA offering has attracted more than 30 teams building data-insight systems with it, with applications in system monitoring, experimentation analysis, and business intelligence, some of which have generated significant revenue uplift.