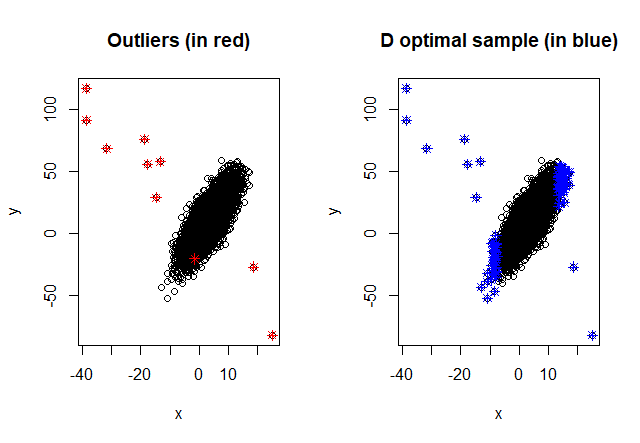
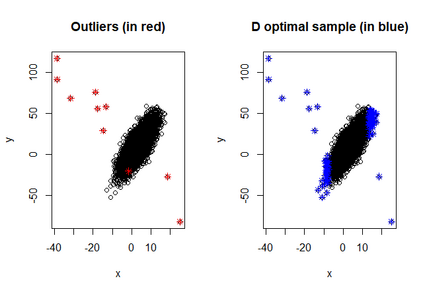
Nowadays, in many different fields, massive data are available and for several reasons, it might be convenient to analyze just a subset of the data. The application of the D-optimality criterion can be helpful to optimally select a subsample of observations. However, it is well known that D-optimal support points lie on the boundary of the design space and if they go hand in hand with extreme response values, they can have a severe influence on the estimated linear model (leverage points with high influence). To overcome this problem, firstly, we propose an unsupervised exchange procedure that enables us to select a nearly D-optimal subset of observations without high leverage values. Then, we provide a supervised version of this exchange procedure, where besides high leverage points also the outliers in the responses (that are not associated to high leverage points) are avoided. This is possible because, unlike other design situations, in subsampling from big datasets the response values may be available. Finally, both the unsupervised and the supervised selection procedures are generalized to I-optimality, with the goal of getting accurate predictions.
翻译:目前,在许多不同的领域,有大量数据,而且出于若干原因,也许可以简单分析数据的一个子集。D-最佳标准的应用有助于最佳地选择观测的子样本。然而,众所周知,D-最佳支持点位于设计空间的边界上,如果它们与极端反应值齐头并进,它们可能对估计的线性模型(影响大的杠杆点)产生严重影响。为了克服这一问题,首先,我们提出一个未经监督的交换程序,使我们能够选择近乎D-最佳的观察子集,而没有高杠杆值。然后,我们提供了这一交换程序的受监督版本,其中除了高杠杆值外,还指明了答复中的外端点(与高杠杆点无关)是避免的。这是可能的,因为与其他设计情况不同的是,在从大数据集的子抽样中可以找到反应值。最后,未经监督和监督的选择程序都普遍化为I-最佳性,目标是获得准确的预测。