Convergence Analysis of Nonlinear Kaczmarz Method for Systems of Nonlinear Equations with Component-wise Convex Mapping

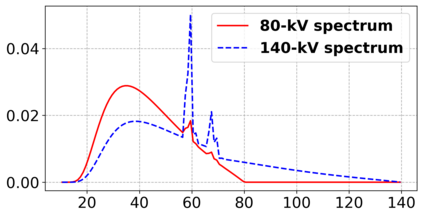
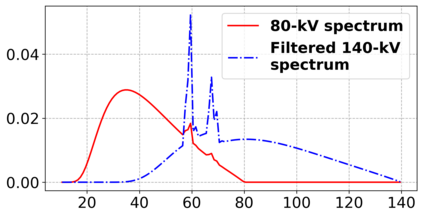
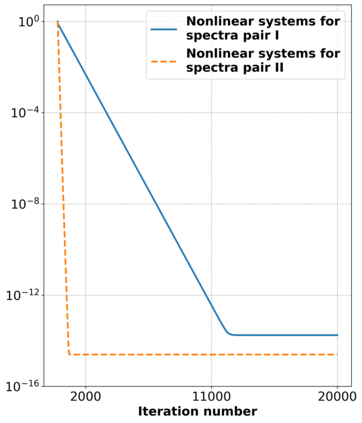
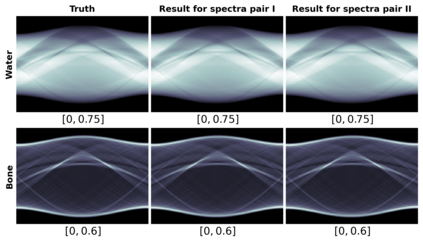
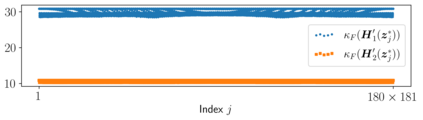
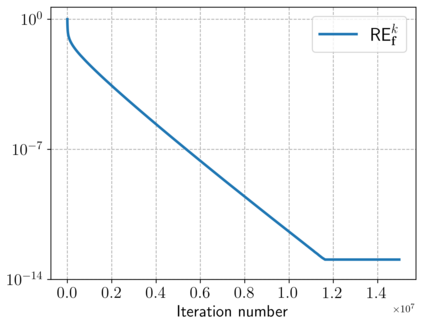
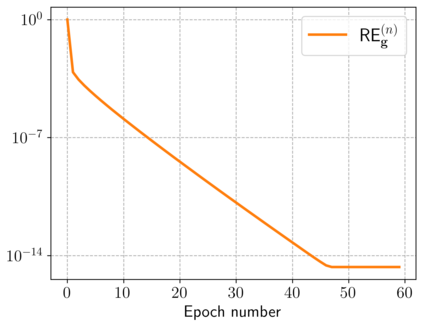
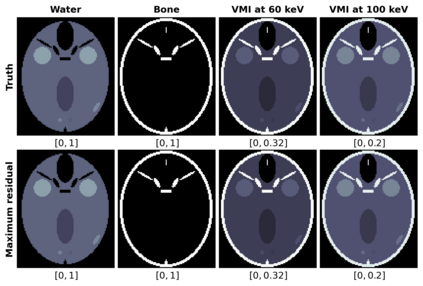
Motivated by a class of nonlinear imaging inverse problems, for instance, multispectral computed tomography (MSCT), this paper studies the convergence theory of the nonlinear Kaczmarz method (NKM) for solving systems of nonlinear equations with component-wise convex mapping, namely, the function corresponding to each equation being convex. Although the tangential cone condition (TCC) is often used to prove the convergence of NKM, it may be impossible or difficult to verify/satisfy this condition for such kind of nonlinear systems. We propose a novel condition named relative gradient discrepancy condition (RGDC), and make use of it to prove the convergence and even the convergence rate of NKM with several general index selection strategies, where these strategies include the cyclic strategy and maximum residual strategy. Particularly, we investigate the application of NKM for solving nonlinear systems in MSCT image reconstruction. We prove that the nonlinear mapping of interest fulfills the proposed RGDC rather than the component-wise local TCC, and provide the global convergence of NKM based on the previously obtained results. Numerical experiments further illustrate the numerical convergence of NKM for MSCT image reconstruction.