Time-reassigned synchrosqueezing frequency-domain chirplet transform for multicomponent signals with intersecting group delay curves

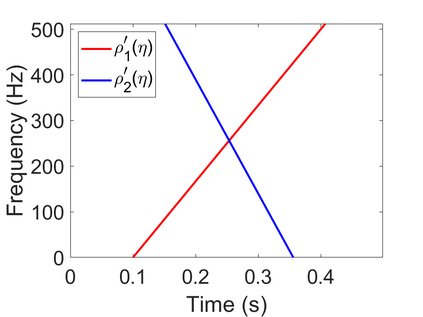
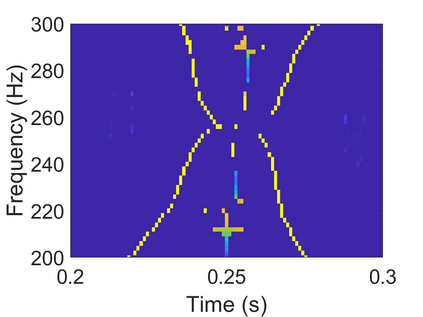
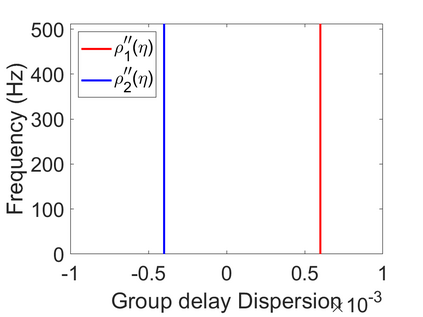
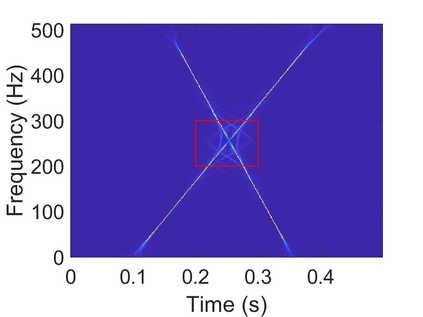
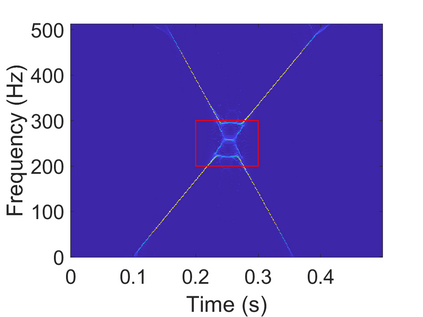
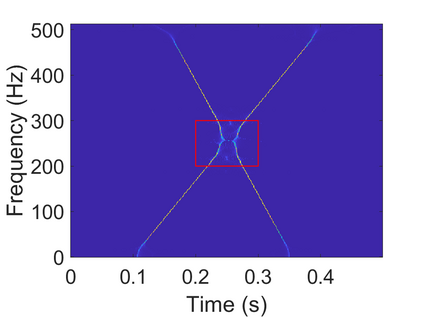
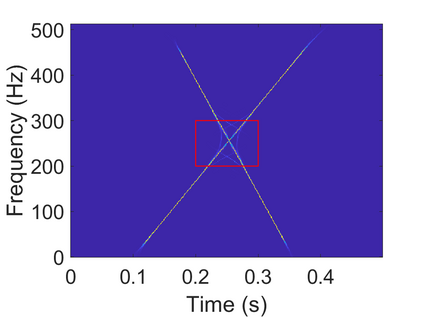
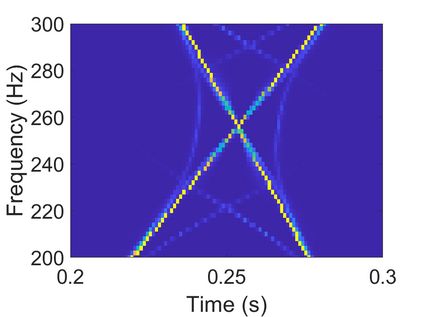
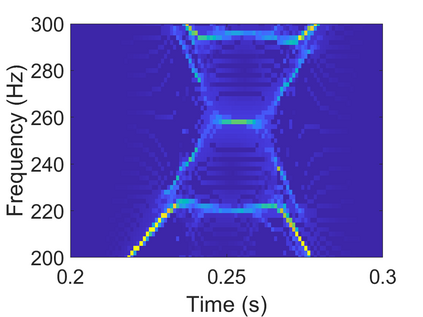
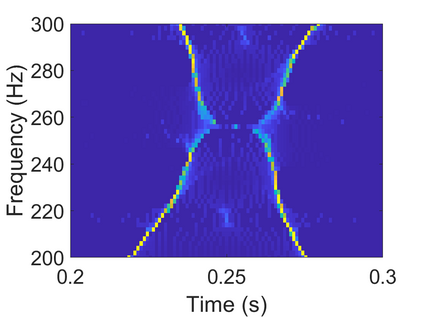
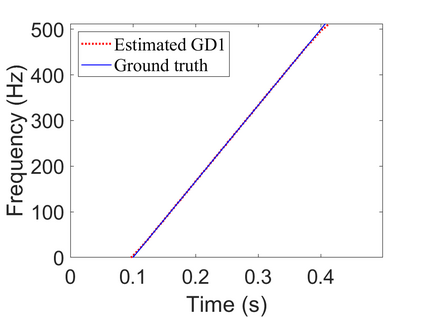
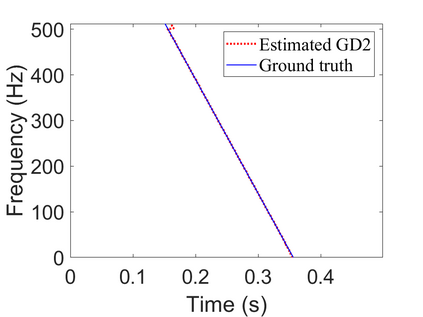
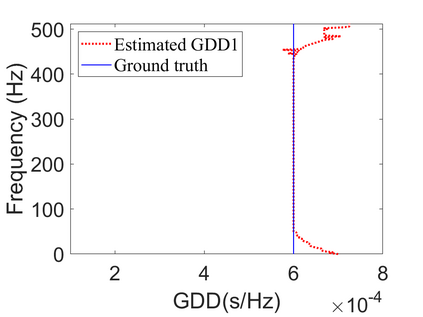
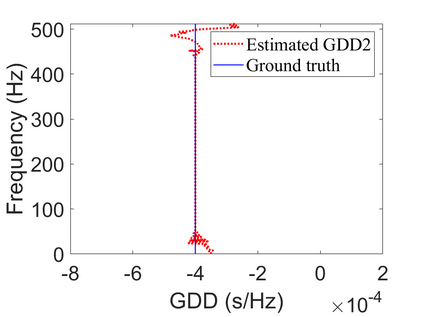
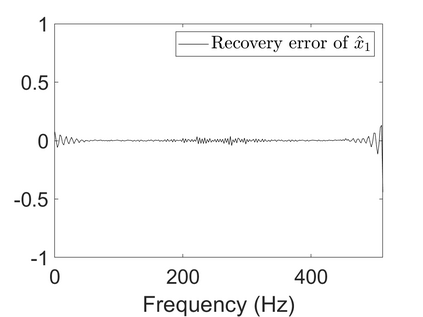
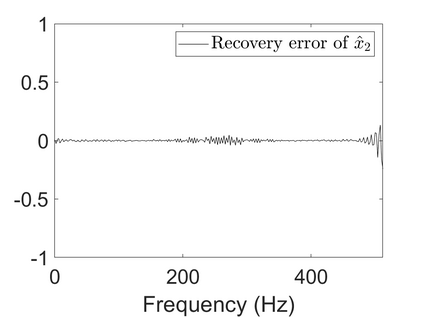
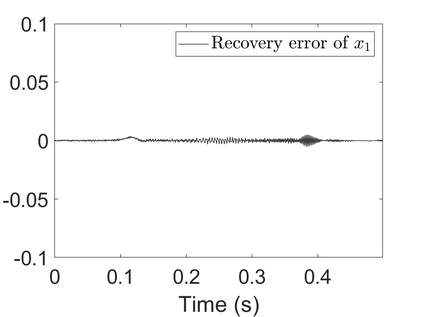
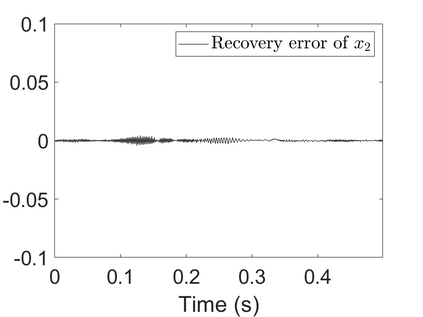
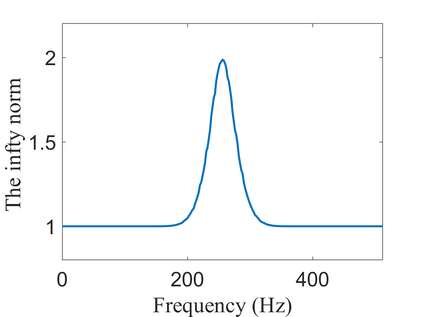
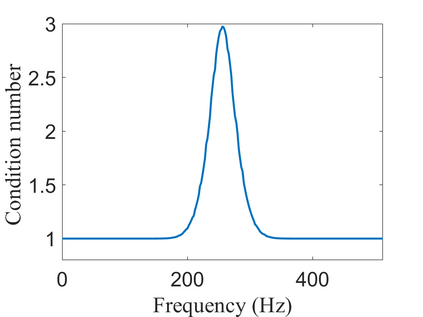
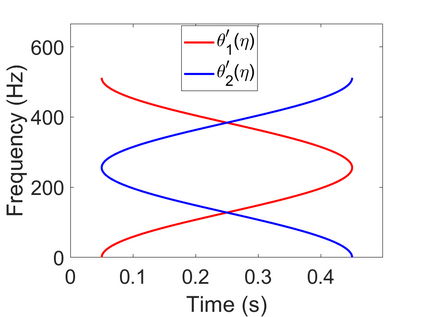
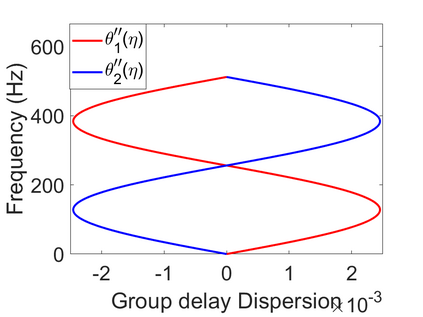
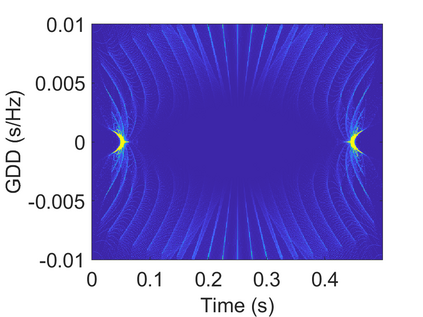
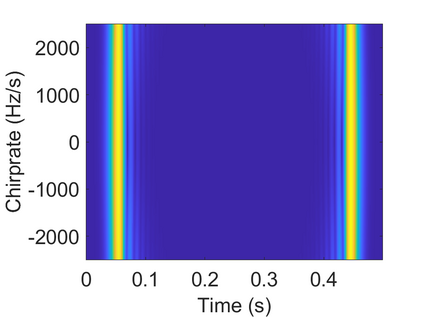
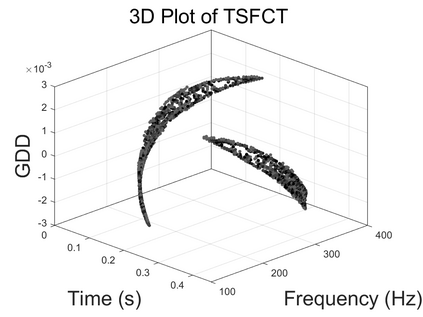
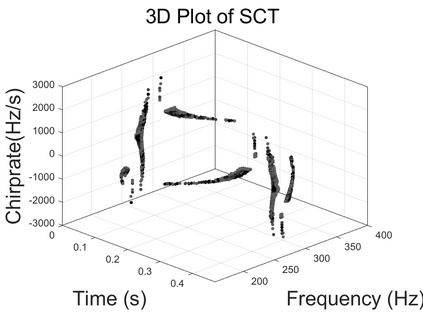
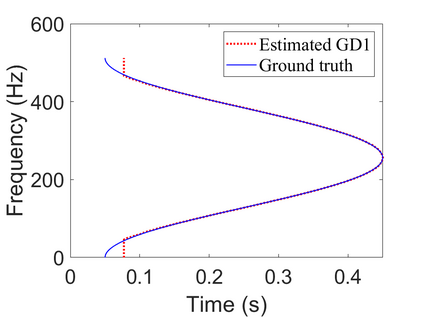
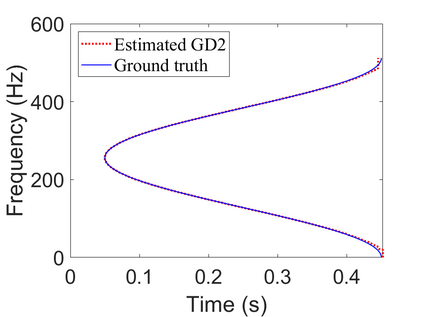
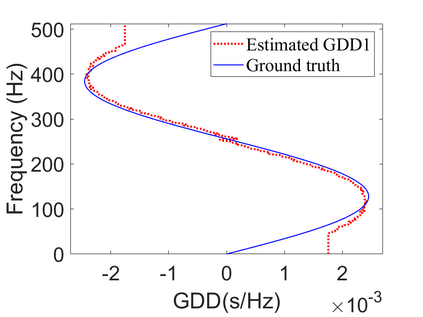
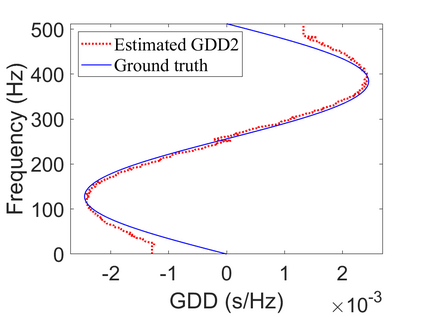
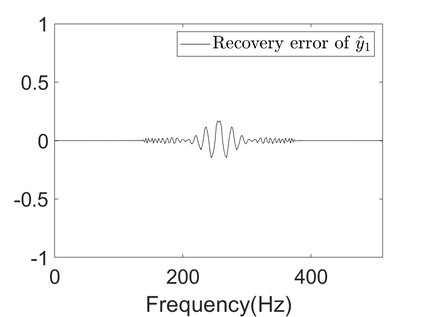
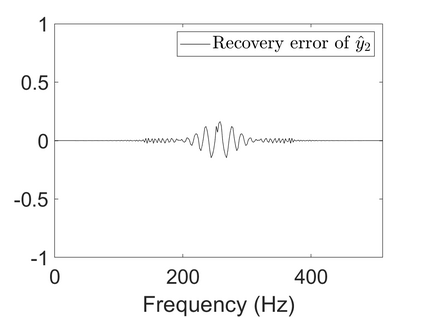
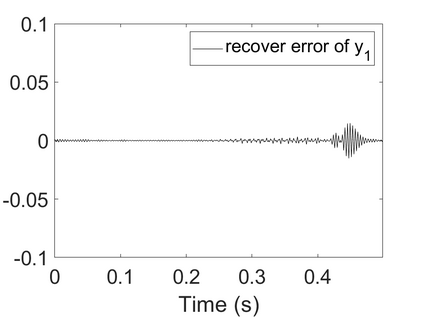
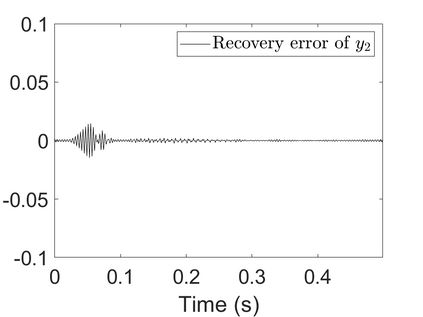
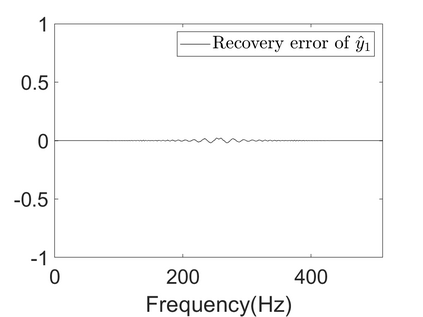
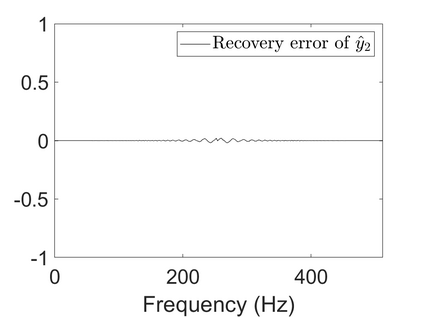
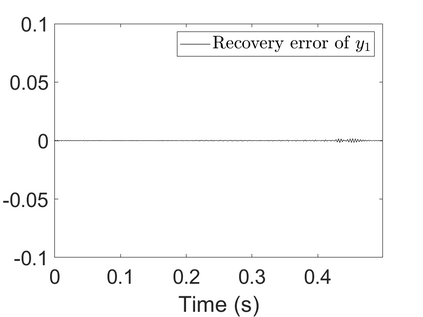
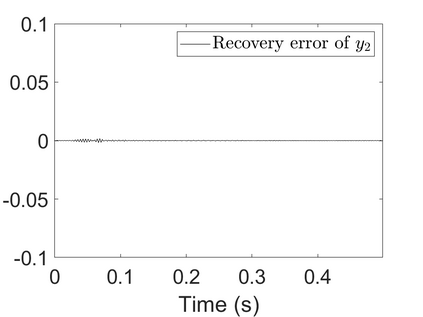
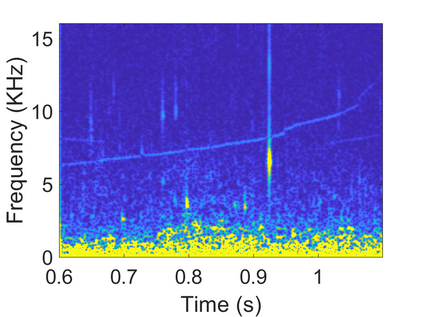
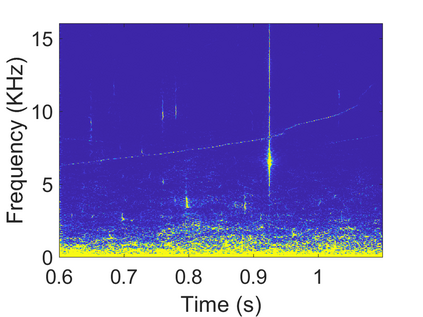
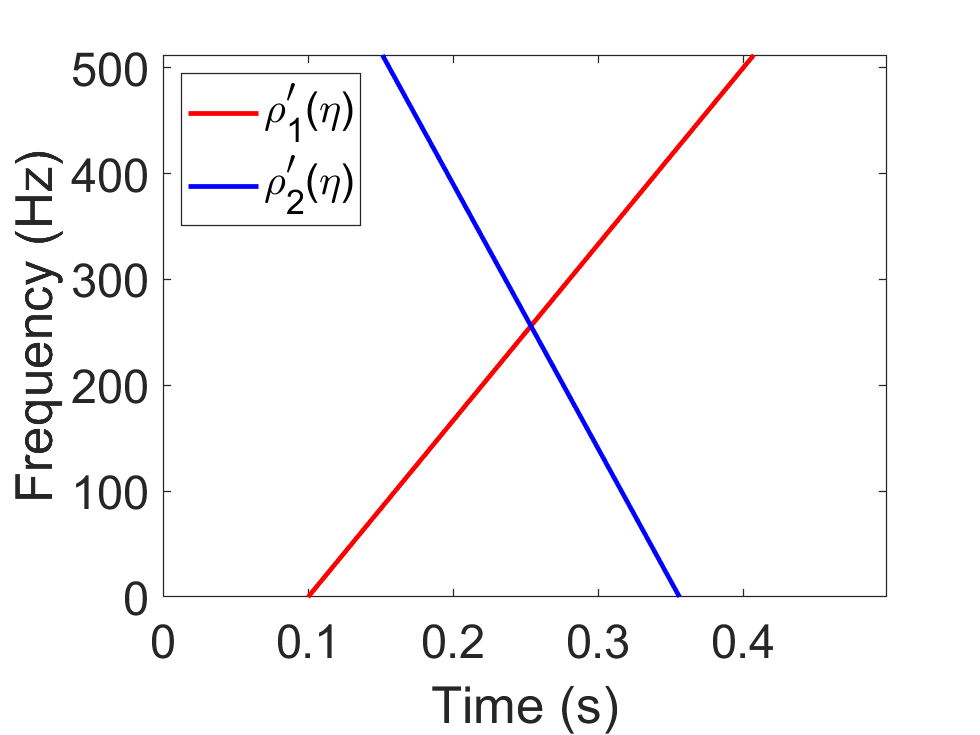
To analyze signals with rapid frequency variations or transient components, the time-reassigned synchrosqueezing transform (TSST) and its variants have been recently proposed. Unlike the traditional synchrosqueezing transform, TSST squeezes the time-frequency (TF) coefficients along the group delay (GD) trajectories rather than the instantaneous frequency trajectories. Although TSST methods perform well in analyzing transient signals, they are fundamentally limited in processing multicomponent signals with intersecting GD curves. This limitation compromises the accuracy of both feature extraction and signal component recovery, thereby significantly reducing the interpretability of time-frequency representations (TFRs). This is particularly problematic in broadband signal processing systems, where the linearity of the phase response is critical and precise measurement of group delay dispersion (GDD) is essential. Motivated by the superior capability of frequency-domain signal modeling in characterizing rapidly frequency-varying signals, this paper proposes a novel three-dimensional time-frequency-group delay dispersion (TF-GDD) representation based on the frequency-domain chirplet transform. A subsequent time-reassigned synchrosqueezing frequency-domain chirplet transform (TSFCT) is introduced to achieve a sharper TF-GDD distribution and more accurate GD estimation. For mode retrieval, a novel frequency-domain group signal separation operation (FGSSO) is proposed.The theoretical contributions include a derivation of the approximation error for the GD and GDD reference functions and an establishment of the error bounds for FGSSO-based mode retrieval. Experimental results demonstrate that the proposed TSFCT and FGSSO effectively estimate GDs and retrieve modes--even for modes with intersecting GD trajectories.