Sparse Regression Faster than $d^ω$

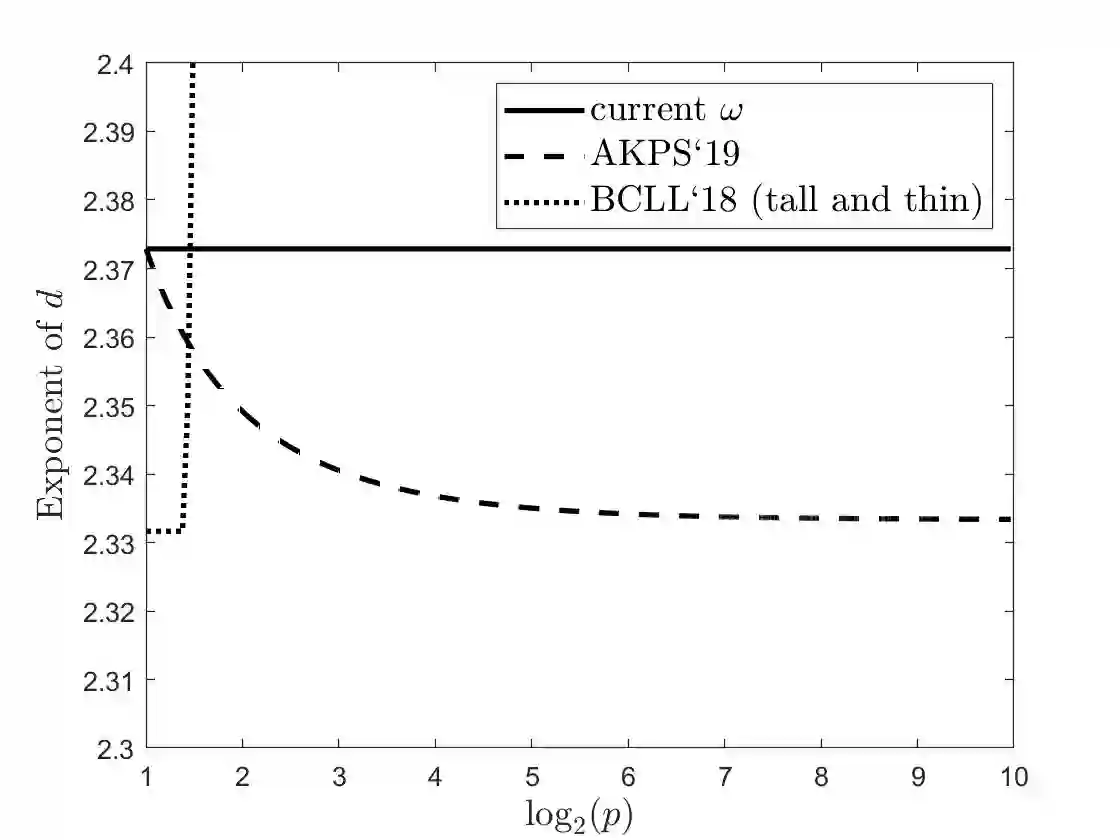
The current complexity of regression is nearly linear in the complexity of matrix multiplication/inversion. Here we show that algorithms for $2$-norm regression, i.e., standard linear regression, as well as $p$-norm regression (for $1 < p < \infty$) can be improved to go below the matrix multiplication threshold for sufficiently sparse matrices. We also show that for some values of $p$, the dependence on dimension in input-sparsity time algorithms can be improved beyond $d^\omega$ for tall-and-thin row-sparse matrices.