Quadratic speedup of global search using a biased crossover of two good solutions

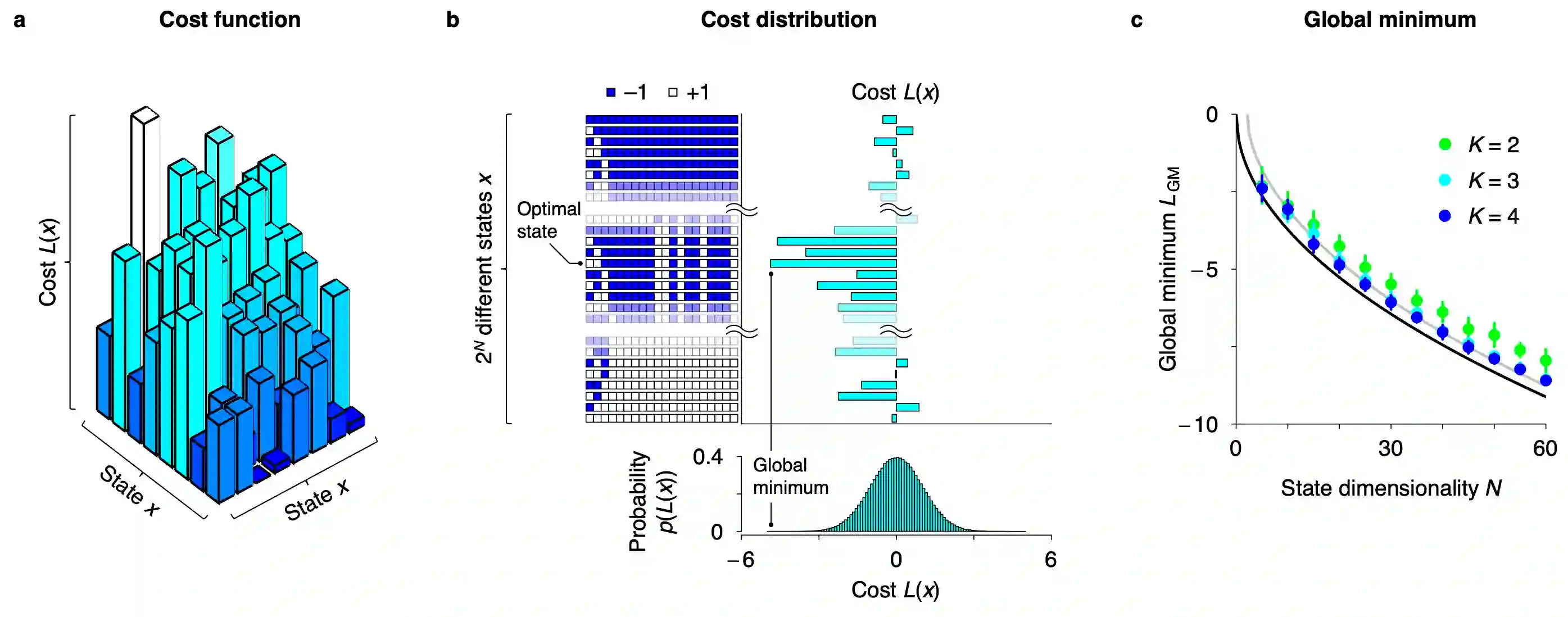
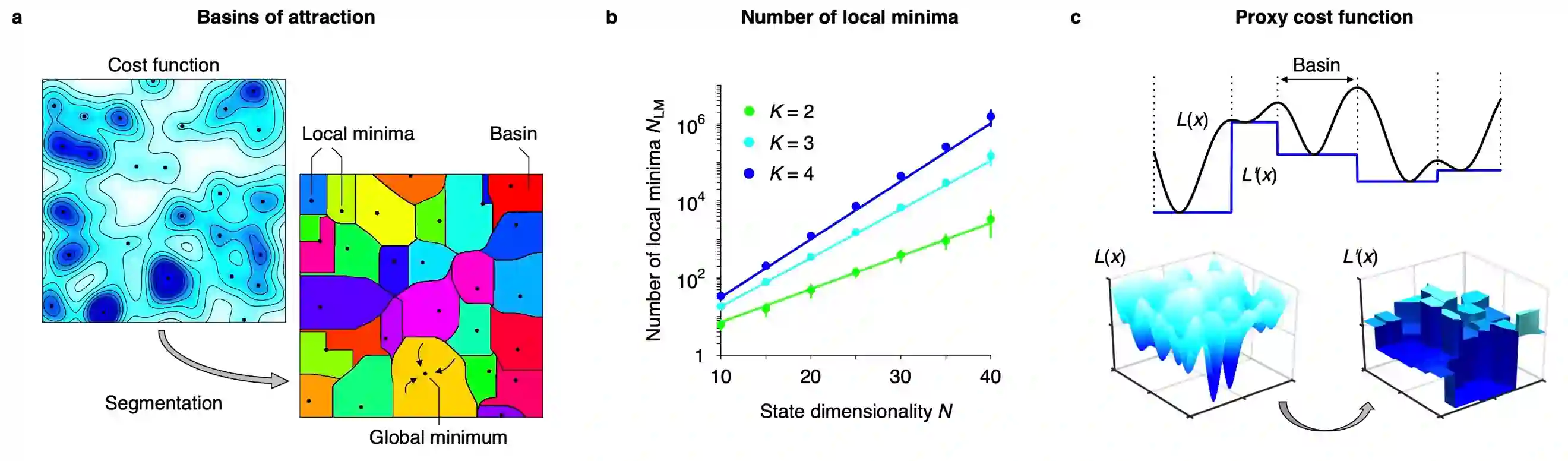
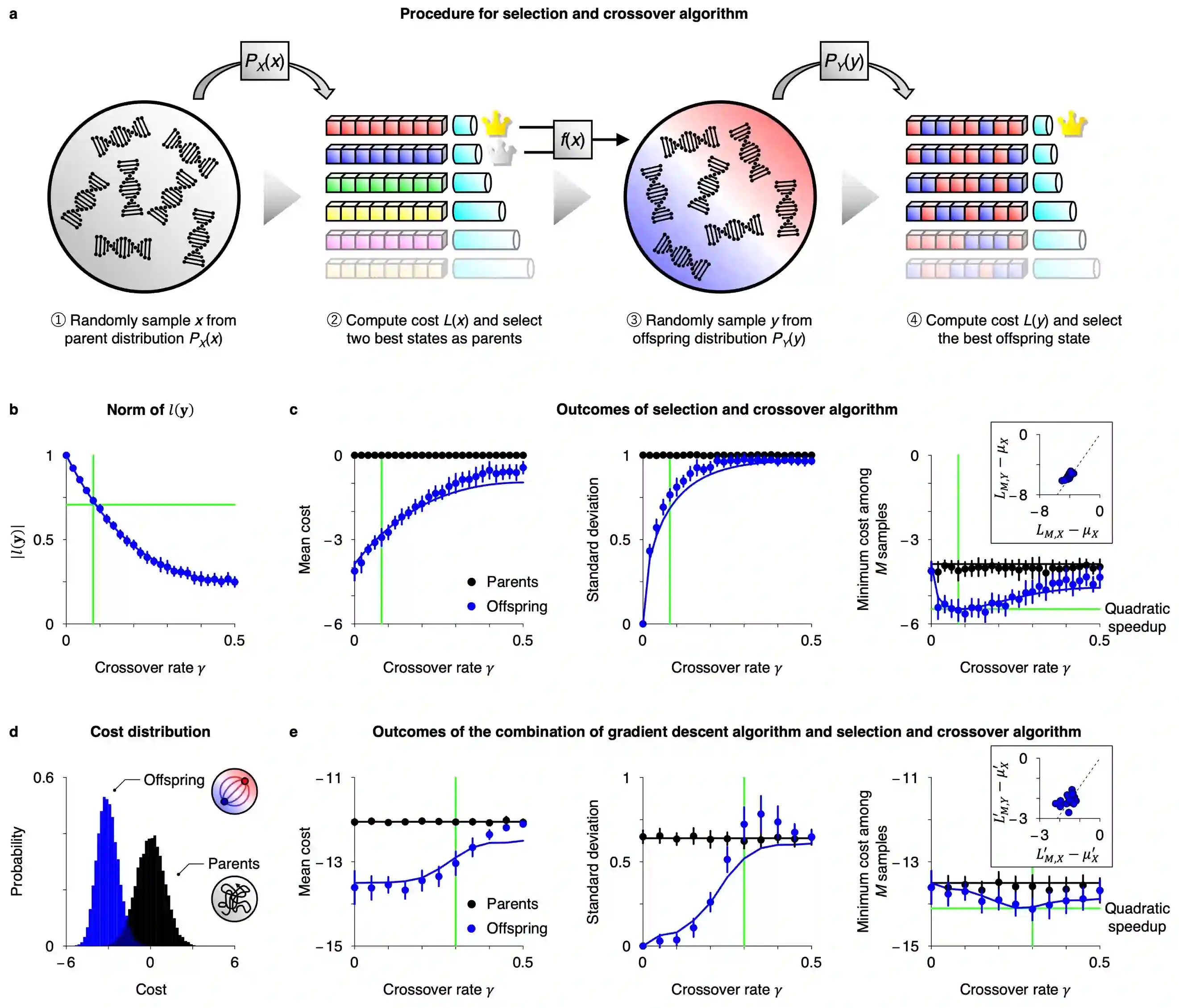
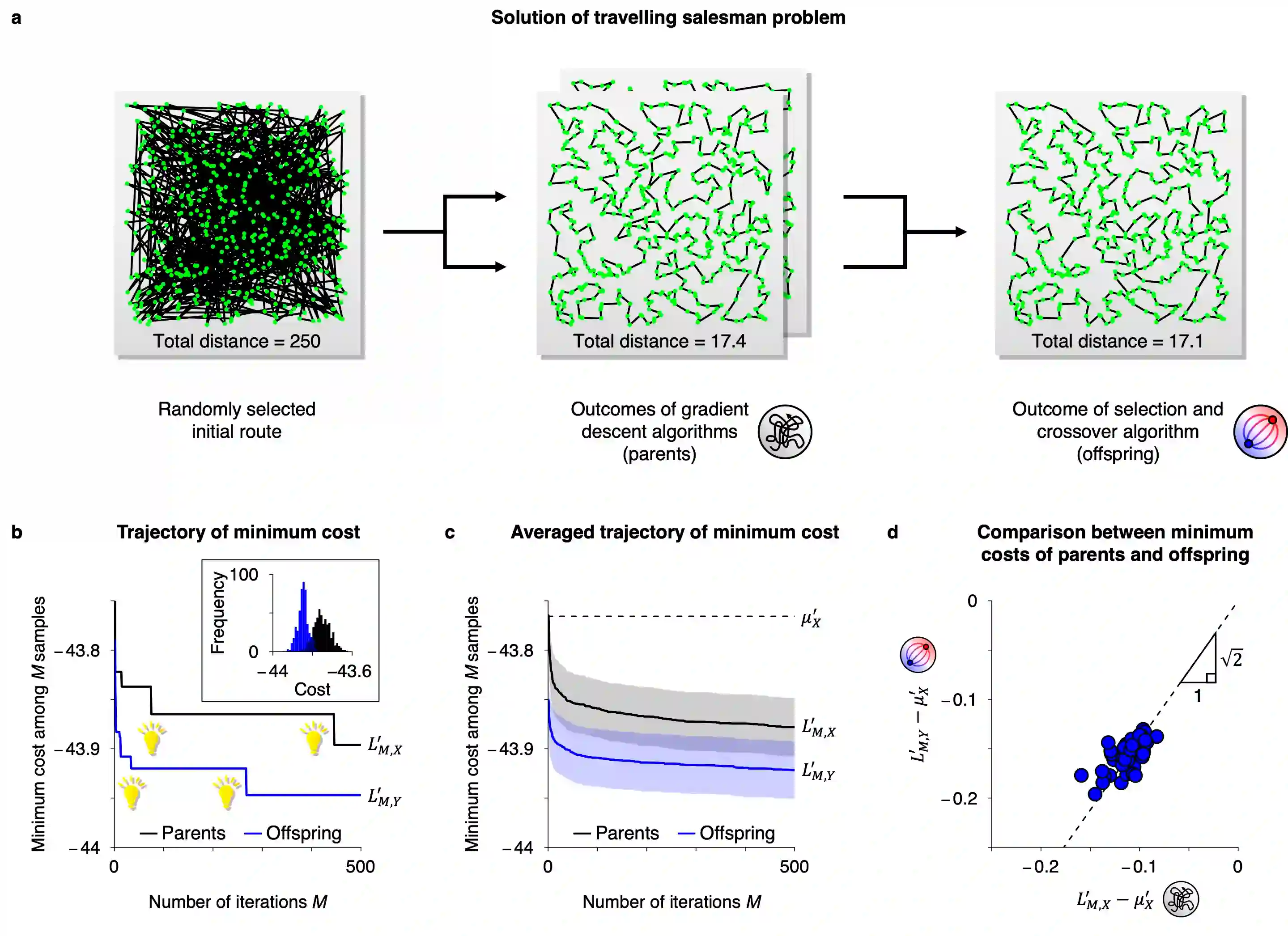
The minimisation of cost functions is crucial in various optimisation fields. However, identifying their global minimum remains challenging owing to the huge computational cost incurred. This work analytically expresses the computational cost to identify an approximate global minimum for a class of cost functions defined under a high-dimensional discrete state space. Then, we derive an optimal global search scheme that minimises the computational cost. Mathematical analyses demonstrate that a combination of the gradient descent algorithm and the selection and crossover algorithm--with a biased crossover weight--maximises the search efficiency. Remarkably, its computational cost is of the square root order in contrast to that of the conventional gradient descent algorithms, indicating a quadratic speedup of global search. We corroborate this proposition using numerical analyses of the travelling salesman problem. The simple computational architecture and minimal computational cost of the proposed scheme are highly desirable for biological organisms and neuromorphic hardware.