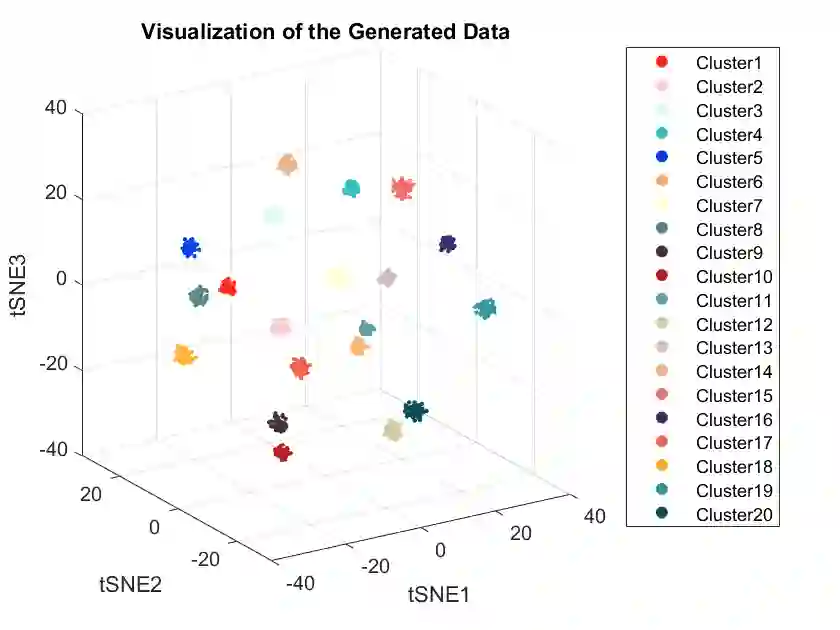
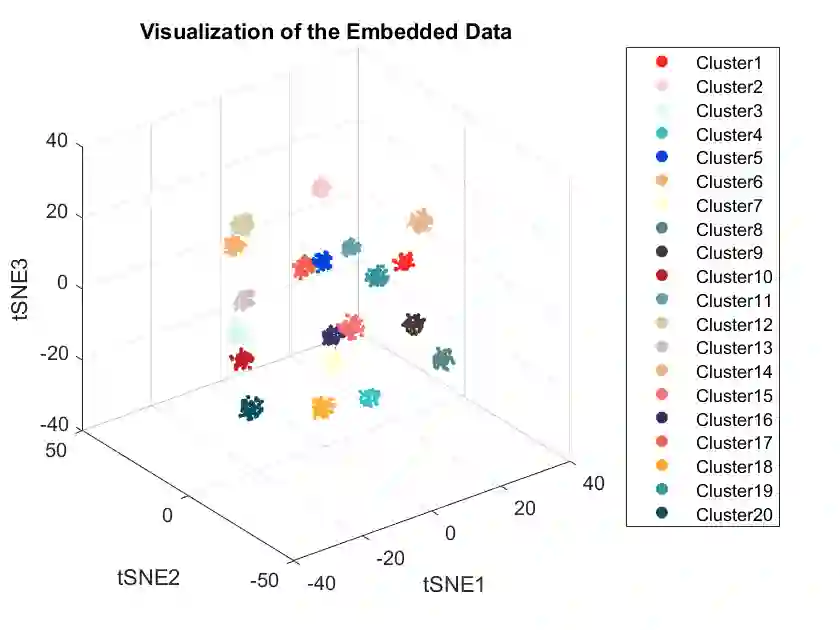
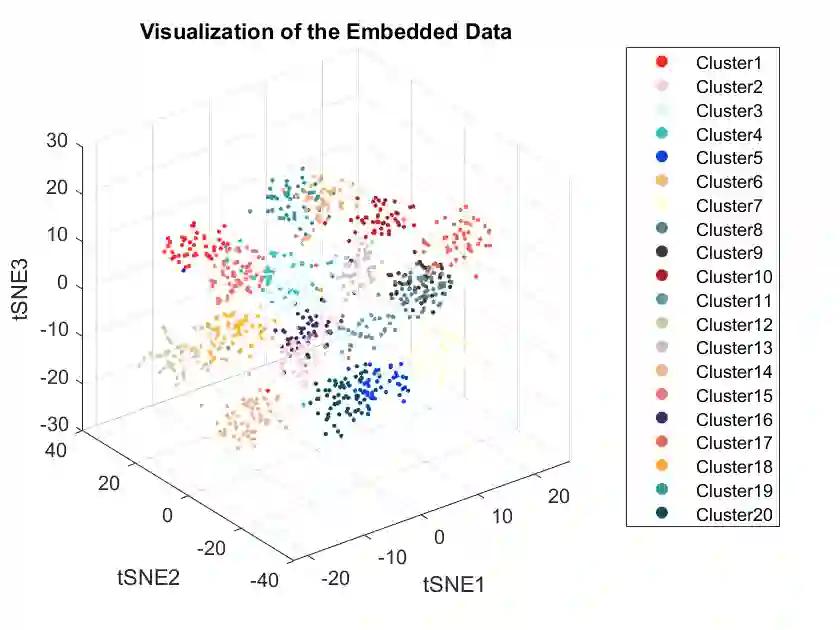
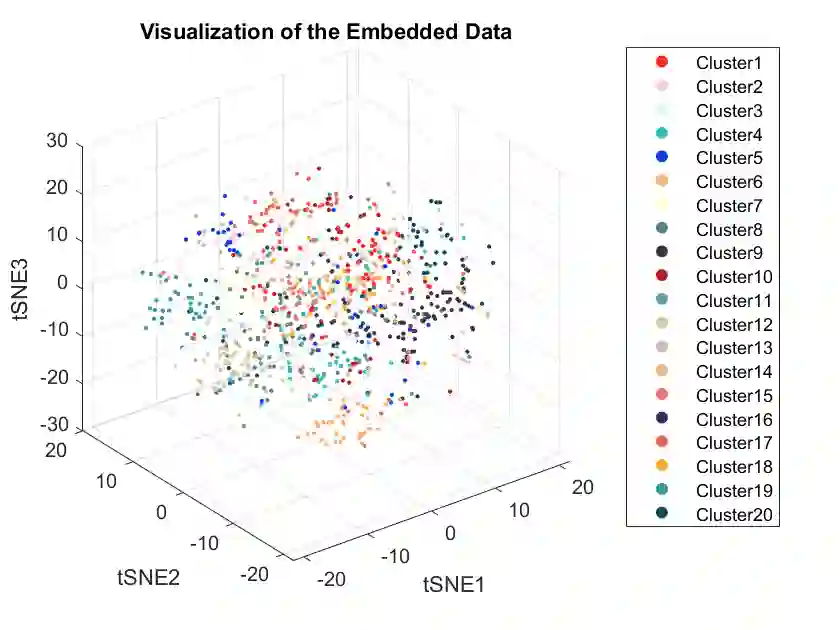
In this paper, we propose a randomly projected convex clustering model for clustering a collection of $n$ high dimensional data points in $\mathbb{R}^d$ with $K$ hidden clusters. Compared to the convex clustering model for clustering original data with dimension $d$, we prove that, under some mild conditions, the perfect recovery of the cluster membership assignments of the convex clustering model, if exists, can be preserved by the randomly projected convex clustering model with embedding dimension $m = O(\epsilon^{-2}\log(n))$, where $0 < \epsilon < 1$ is some given parameter. We further prove that the embedding dimension can be improved to be $O(\epsilon^{-2}\log(K))$, which is independent of the number of data points. Extensive numerical experiment results will be presented in this paper to demonstrate the robustness and superior performance of the randomly projected convex clustering model. The numerical results presented in this paper also demonstrate that the randomly projected convex clustering model can outperform the randomly projected K-means model in practice.
翻译:本文提出了一种随机投影凸聚类模型,用于聚类在$\mathbb{R}^d$中的$n$个高维数据点,其中隐藏着$K$个聚类。与用$d$维原始数据聚类的凸聚类模型相比,我们证明,在一些温和条件下,如果凸聚类模型的完美恢复存在,那么随机投影凸聚类模型可以通过嵌入维度$m=O(\epsilon^{-2}\log(n))$来保留聚类成员分配的完美恢复,其中$0<\epsilon<1$是某个给定的参数。我们进一步证明,嵌入维度可以改进为$O(\epsilon^{-2}\log(K))$,这与数据点数量无关。本文还将展示大量数值实验结果,以展示随机投影凸聚类模型的稳健性和卓越性能。本文中呈现的数值结果还表明,在实践中,随机投影凸聚类模型可以优于随机投影K均值模型。