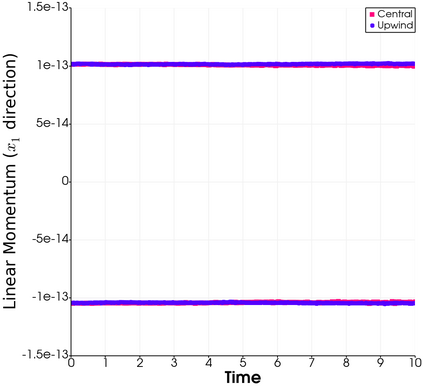
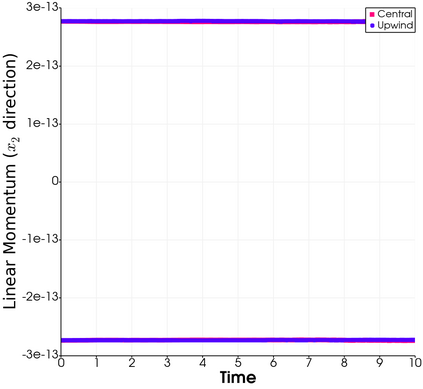
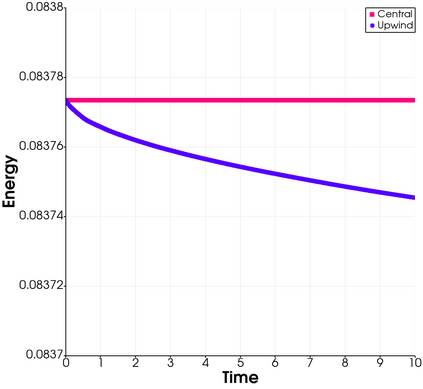
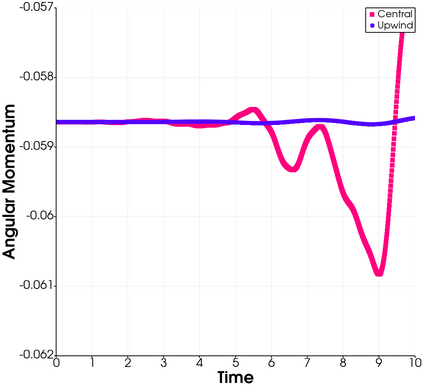
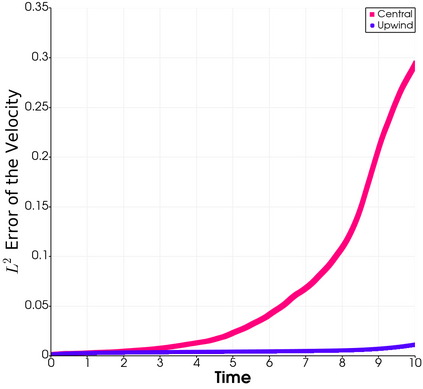
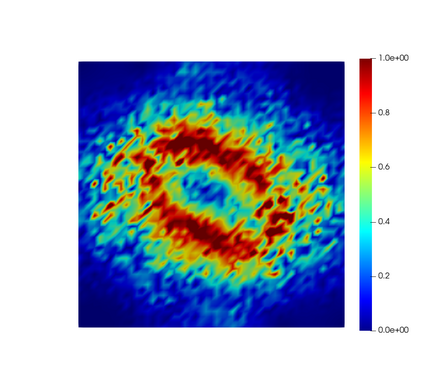
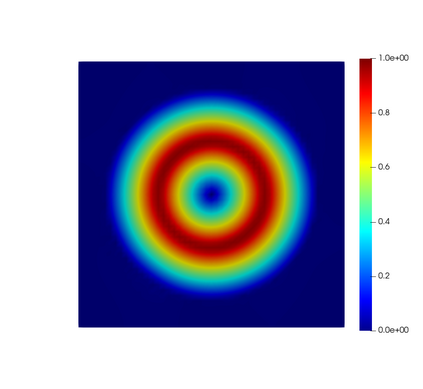
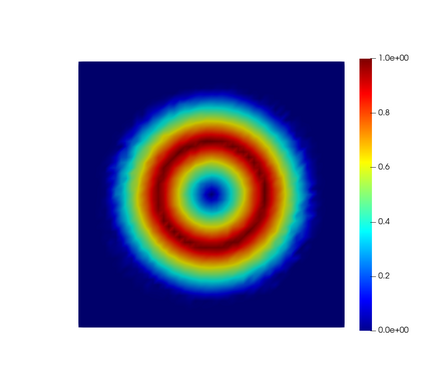
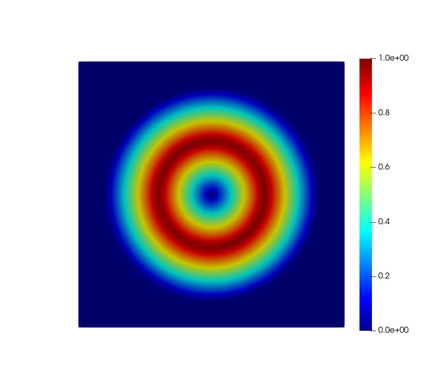
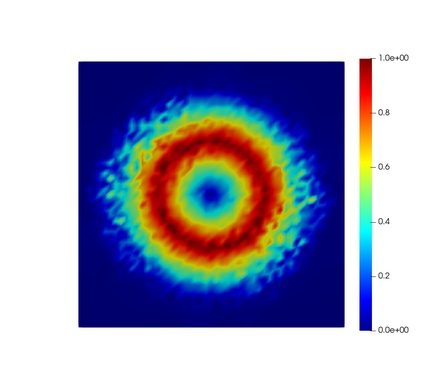
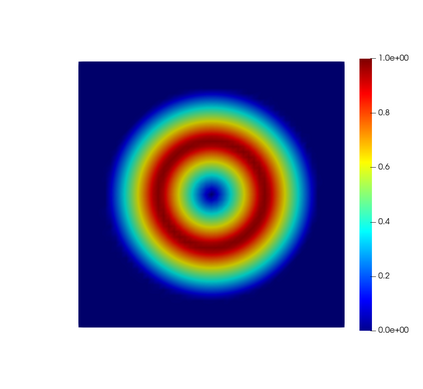
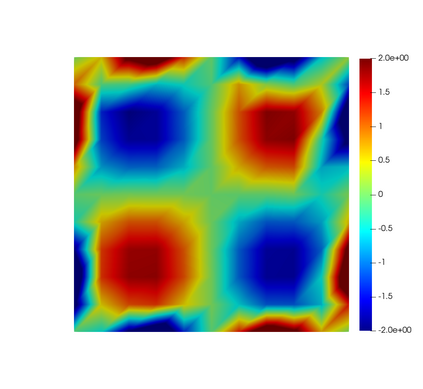
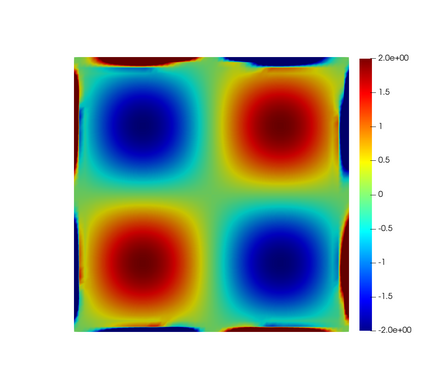
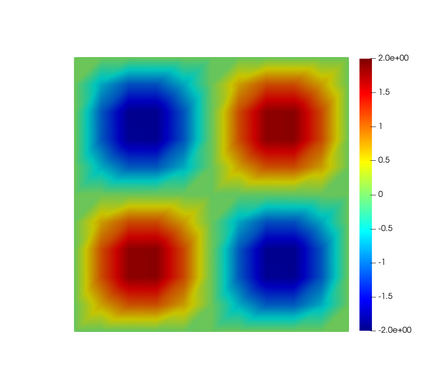
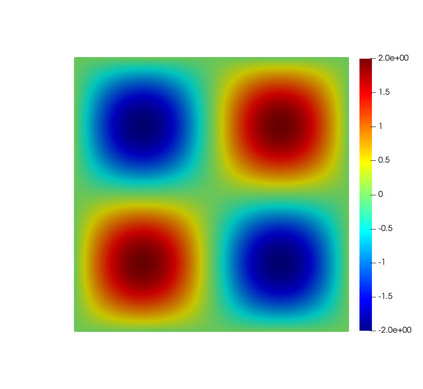
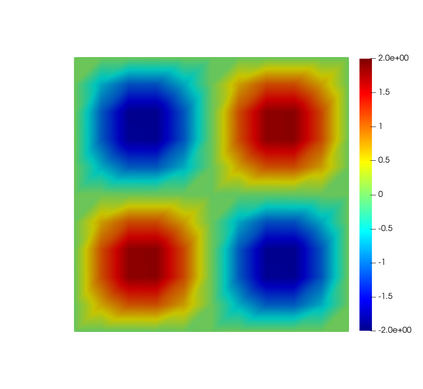
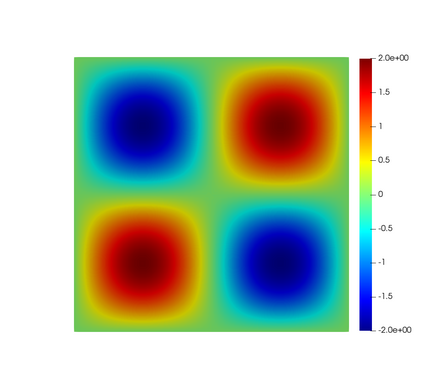
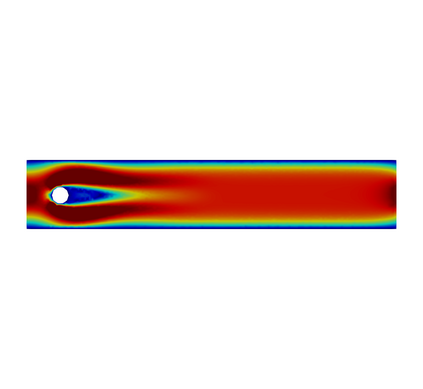
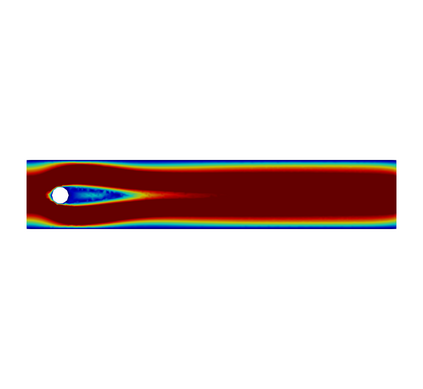
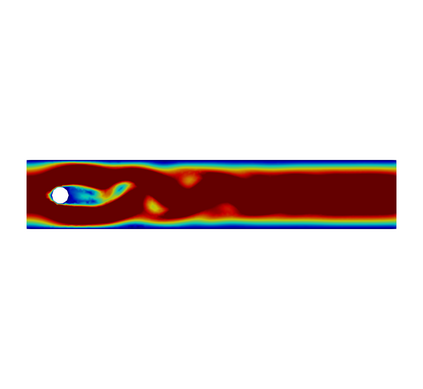
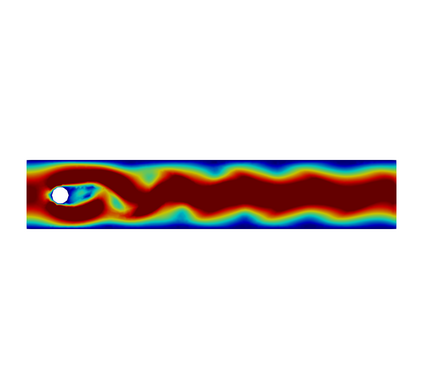
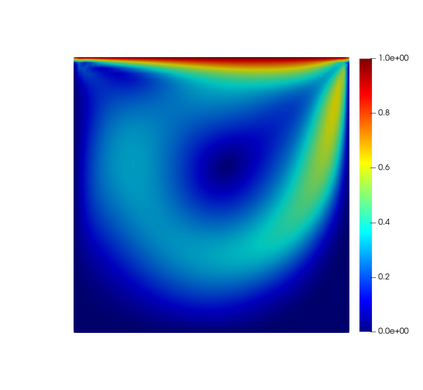
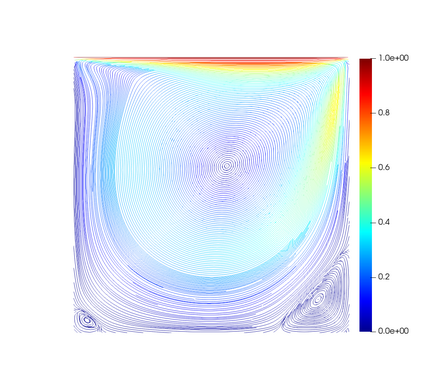
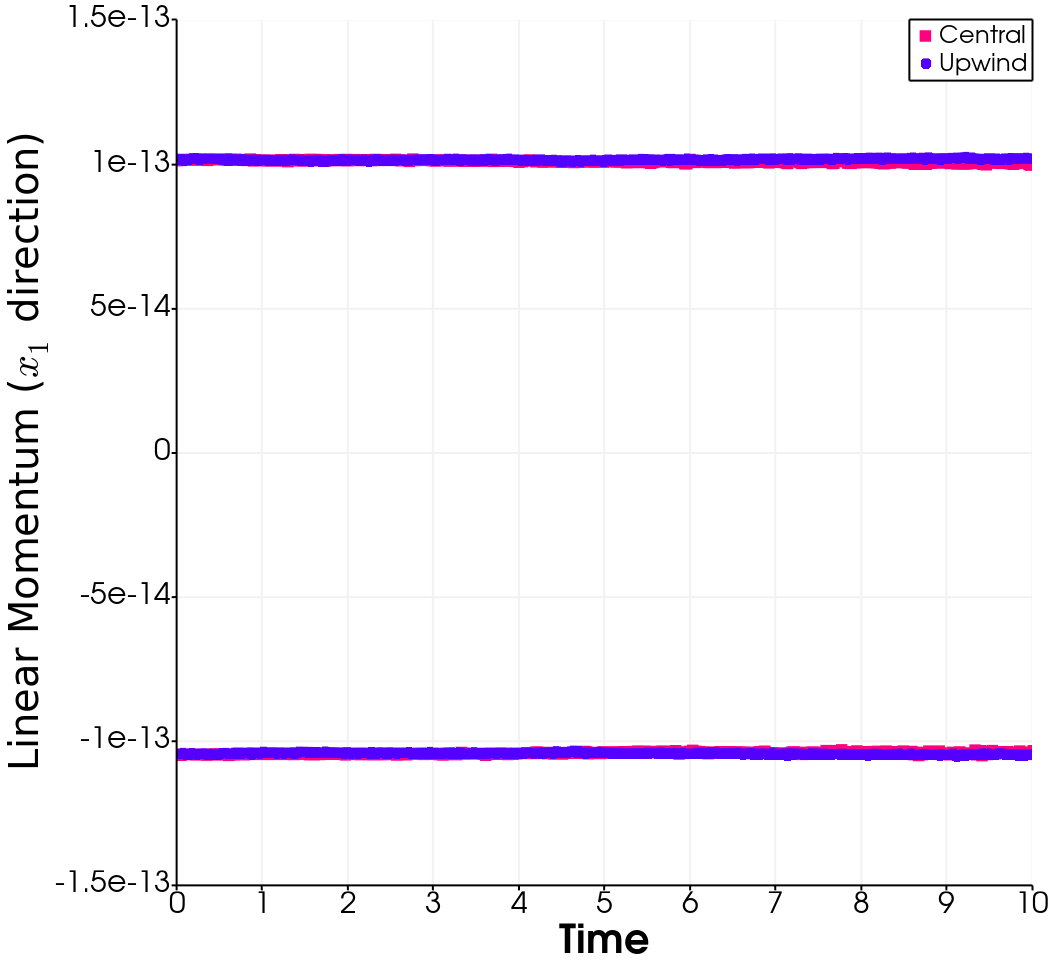
In this paper, we present consistent and inconsistent discontinuous Galerkin methods for incompressible Euler and Navier-Stokes equations with the kinematic pressure, Bernoulli function and EMAC function. Semi- and fully discrete energy stability of the proposed dG methods are proved in a unified fashion. Conservation of total energy, linear and angular momentum is discussed with both central and upwind fluxes. Numerical experiments are presented to demonstrate our findings and compare our schemes with conventional schemes in the literature in both unsteady and steady problems. Numerical results show that global conservation of the physical quantities may not be enough to demonstrate the performance of the schemes, and our schemes are competitive and able to capture essential physical features in several benchmark problems.
翻译:在本文中,我们用一致和不一致的Galerkin方法,处理不压抑的尤勒和纳维埃-斯托克斯等式与运动压力、伯努利功能和EMAC功能等同,以统一的方式证明拟议dG方法的半分离和完全分离的能源稳定性,与中风和上风通量讨论保护总能量、线性和角性动力的问题,在不稳定和稳定的问题中进行数字实验,以展示我们的调查结果,并将我们的计划与文献中的常规计划进行比较。数字结果显示,全球对物理数量的养护可能不足以显示计划的业绩,我们的计划具有竞争力,能够在几个基准问题中捕捉到基本的物理特征。
相关内容
Source: Apple - iOS 8