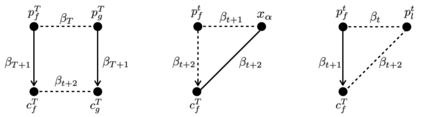
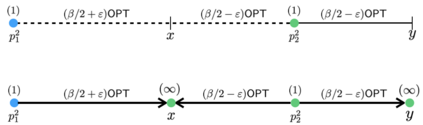
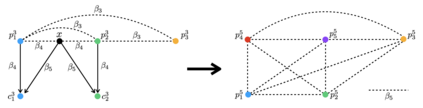
We consider the online $k$-median clustering problem in which $n$ points arrive online and must be irrevocably assigned to a cluster on arrival. As there are lower bound instances that show that an online algorithm cannot achieve a competitive ratio that is a function of $n$ and $k$, we consider a beyond worst-case analysis model in which the algorithm is provided a priori with a predicted budget $B$ that upper bounds the optimal objective value. We give an algorithm that achieves a competitive ratio that is exponential in the the number $k$ of clusters, and show that the competitive ratio of every algorithm must be linear in $k$. To the best of our knowledge this is the first investigation in the literature that considers cluster consistency using competitive analysis.
翻译:我们考虑在线$k$-中位数聚类问题,即有$n$个点在线到达,必须在到达时不可逆地分配到一个聚类中。由于存在下界实例表明,在线算法不能实现一个关于$n$和$k$的竞争比例的函数,因此我们考虑一种超越最坏情况的分析模型,其中算法预先提供了一个预测预算$B$,可以上限最优目标值。我们提出了一个算法,该算法的竞争比例在聚类数$k$的指数级别上,同时证明每个算法的竞争比例必须是$k$的线性函数。据我们所知,这是文献中第一次使用竞争分析来考虑一致的聚类问题。