强化学习初探 - 从多臂老虎机问题说起

▌背景和问题定义

---

---

2018年我开始了机器学习相关领域的博士生涯，相比于目前流行的深度学习以及类似的需要大量训练数据来生成模型的监督学习方法，强化学习一个重要的不同点是利用训练的数据去评估（evaluate）下一步的行动（action），而不是仅仅指示（instruct）出正确的行动。 导师提供了一个有趣的问题作为切入点来深入理解“强化学习”，那就是多臂老虎机问题（multi-armed bandit）。

多臂老虎机实验本质上是一类简化的强化学习问题，这类问题具有非关联的状态（每次只从一种情况输或赢中学习），而且只研究可评估的反馈。假设有一台N个摇臂老虎机，每拉一个摇臂都会有一定的概率获得回报，这样我们有了N种可能的行动（每个摇臂对应一种action），并且每次行动的结果只和当前的状态关联而不受历史行动的结果影响（每次拉摇臂的回报只和老虎机设置的概率相关，之前输赢的结果不会影响本次行动）。我们可以正式定义这种问题是具有单一状态的马尔科夫决策过程【1】。

我们玩了一轮后发现其中一个摇臂回报最好，接下来该如何玩？这里也涉及强化学习一个有趣的主题：“如何在探索（exploration）和利用（exploitation）之间找到更好的平衡”。我们的目标是通过探索和利用使收益最大化，多年来有多种算法被应用到这类问题中，在接下来的部分我会展示几种策略，并提供python的实现【2】来验证每种策略的表现。

▌策略分析与实验

---

---

实验部分我们以N=3为例，并且设定老虎机的回报满足伯努利分布【3】，即回报结果为0/1. 在初始状态S0时，三个摇臂（A、B、C）每次回报为1的概率分别是30%, 50%和80%.

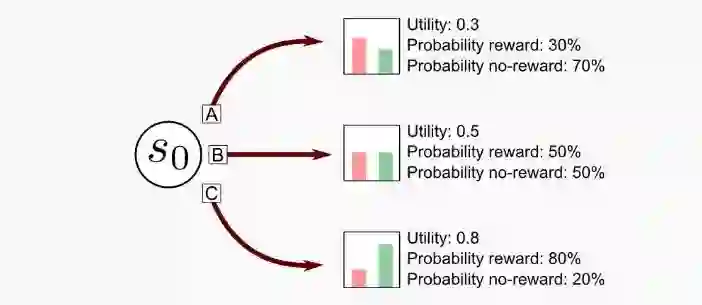
针对每种策略我们在每一轮运行1000次的拉摇臂行为，一共模拟2000轮。这里我们用平均回报总数来衡量利用（exploitation）的表现，如果每轮的回报值是Rn，则平均回报总数=(R1+R2+....+R2000)/2000。

同时我们用实验统计的每个摇臂的回报率与真实回报率的方均根差【4】（RMSE）来评估探索（exploration）的表现。

import numpy as npdef return_rmse(predictions, targets):
    """Return the Root Mean Square error between two arrays    @param predictions an 
array of prediction values    @param targets an array of target values   
 @return the RMSE    """
    return np.sqrt(((predictions - targets)**2).mean())

如果平均回报总数和方均根差都很低，可以认为该策略是偏重探索的策略；反之如果两者结果都很高，则是偏重利用的策略。

下面我们来看几种实验的策略：

1.全知全能（Omniscient）

假设你已经知道回报率80%的那台老虎机，那最直接的策略就是一直玩这一台，每一轮玩1000次后回报应该是800. 这里列出该策略也是先明确一下平均回报总数的上界，后面的每个策略的探索表现都会和这个上界值来比较。

2. 随机（Random）算法

随机策略是最直接的一种方法，像一个无知的赌徒一样每一轮随机地去拉一个摇臂。

这里我们初始化了一个 MultiArmedBandit类的实例 mybandit, 每一次随机生成摇臂的编号（0/1/2），然后调用mybandit.step(action)去模拟拉摇臂的动作,返回此次行为的回报。

from multi_armed_bandit import MultiArmedBandit
import numpy as np

my_bandit = MultiArmedBandit(reward_probability_list=[0.3, 0.5, 0.8])
tot_arms = 3
tot_steps = 1000
cumulated_reward = 0
print("Starting random agent...")
for step in range(tot_steps):
    action = np.random.randint(low=0, high=tot_arms)
    reward = my_bandit.step(action)
    cumulated_reward += reward
print("Cumulated Reward: " + str(cumulated_reward))

以上的程序执行了一轮的模拟（1000次拉摇臂的行为），一轮结束后将回报总数存到cumulatedreward中。针对随机策略，实际上是每个摇臂都有1/3的概率被选到，所以拉1000次摇臂后理论上结果应该接近与（300+500+800）/  3 = 533.3。每一轮的统计结果可能有一些小波动，所以我们运行2000轮模拟计算平均回报总数来中和这些波动。以下是2000轮之后的结果，完整代码请见github中的random_agent_bandit.py文件【5】。

Average Cumulated Reward: 533.441
Average utility distribution: [0.29912987  0.50015673  0.80060398]
Average utility RMSE: 0.000618189621201

这里的平均回报总数已经非常接近理论上的回报值了，同时RMSE也非常的低，说明该策略过于偏重探索，在利用方面相较于最优的回报800是明显失衡的。

3. 贪婪（Greedy）算法

这也是一种很直接的策略，先把所有的摇臂都拉一次，然后选择回报最好的老虎机一直玩下去。这种策略很明显不鼓励进行探索，而且很容易被每个摇臂第一遍的回报结果误导。同样在2000轮模拟，每轮拉1000次的程序（greedy_agent_bandit.py【6】）运行后，结果如下：

Average cumulated reward: 733.153
Average utility distribution: [0.14215225  0.2743839   0.66385142]
Average utility RMSE: 0.177346151284

测试结果明显高于之前的随机策略，尽管如此，RMSE的结果接近0.18，说明在探索方面是失衡的。

4. ϵ-贪婪(Epsilon-greedy)算法

该策略结合了之前两种算法，通过设置一个较小的ϵ值，玩家在每次选择摇臂时，选择当前回报最高的摇臂去玩的概率是1-ϵ（即exploitation的概率），而随机选择任意一个摇臂的概率是ϵ（即exploration的概率）。ϵ的值通常设置为0.1，模拟程序（epsilon_greedy_agent_bandit.py【7】）运行的结果如下：

Average cumulated reward: 763.802
Average utility distribution: [0.2934227   0.49422608  0.80003897]
Average utility RMSE: 0.00505307354513

平均回报的结果要高于之前的策略，而且RMSE的值也降到了0.005，说明在随机的探索有效的收敛到了接近真实的回报概率分布，该策略维持了较好的平衡。

5. Softmax-贪婪（Softmax-greedy）算法

在前一种ϵ-贪婪策略中，玩家在探索时总是按相同的概率随机选择一个摇臂，而使用softmax方法【8】探索新的摇臂时，可能获取更多回报的摇臂会有更大的概率被选中。softmax的函数实现如下：

def softmax(x):

    @param x the input array with each arm's current reward probability
    @return the softmax array with each arms's possible selection probability
    """
    return np.exp(x - np.max(x)) / np.sum(np.exp(x - np.max(x)))

在实验中，我们设置一个 σ 值，使玩家利用当前回报最高的摇臂的概率是σ，而继续探索的概率是1 - σ。在探索时，根据当前每个摇臂的回报率，我们通过softmax函数计算出一个概率分布[p1, p2, p3], 基于此分布来选取下一步要探索的摇臂。这种采样方式相当于在探索中有更高概率选取回报率较高的摇臂，即在探索中不忘利用。在模拟程序（softmax_agent_bandit.py【9】）中，σ = 0.1，运行的结果：

Average cumulated reward: 767.249
Average utility distribution: [0.29169784  0.49047397  0.79968229]
Average utility RMSE: 0.00729776356239

可以看出利用的结果比前一种策略(Epsilon-greedy)稍好一点，但探索的错误率却较之略高（0.007 vs 0.005）。可见探索与利用之间的平衡关系很微妙也很脆弱。

6. ϵ-下降(Epsilon-decreasing)算法

在Epsilon-greedy算法中我们设置了固定的ϵ = 0.1，这不是一个理想的选择， 因为经过多次测试后，我们已经得到了所有摇臂相对准确的回报率的分布估计，此时我们应该适当减少探索，即降低epsilon的值，使得利用当前最好回报的摇臂的概率增加。这里我们设置初始的ϵ = 0.1，并采用线性下降的方法使得ϵ最后降到0.0001，使得在每轮1000次测试中，从开始最多10%的概率去探索到最后一次几乎完全变为利用（此时ϵ 接近于 0）。这种策略下程序（epsilon_decreasing_agent_bandit.py【10】）运行的结果：

Average cumulated reward: 777.423
Average utility distribution: [0.28969042  0.48967624  0.80007298]
Average utility RMSE: 0.00842363169768

平均回报略高于之前的策略，但错误率也变高了。这样的结果再一次印证了利用和探索之间微妙的平衡关系。感兴趣的读者可以尝试更快的下降方法，如指数级的下降，这样的策略会更多偏向于利用，理论上应该有更好的回报，但RMSE的错误率会更高。

7. 汤普森采样（Thompson sampling【11】）

理解该策略需要概率论和贝叶斯统计的一些知识，尤其是常见的概率分布和贝叶斯定理的基本原理。在本实验中，我们通过拉一个摇臂赢和输的次数来评估所谓的效用函数，从统计学角度来说该效用函数就是多臂老虎机的伯努利回报分布的一个近似估计。

在频率论统计中伯努利分布是通过最大似然估计【12】来计算的：

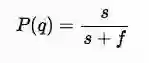
其中P(q)代表某个摇臂取得正回报的概率， s 是赢的次数，f是输的次数。这里最大似然估计有一个明显的问题就是在只有少量实验样本的时候回报概率的结果会有很大的偏差。

这样问题就变成了基于目前已有的实验数据，如何找到一个优化的伯努利分布的近似估计。利用贝叶斯方法，我们可以定义当前各摇臂的回报率分布为先验分布，进而通过计算下一步行动的最佳后验概率去采样下一步的行动，这种方法就叫汤普森采样法， 由William Thompson在1933年发表。下面我们根据实验设定简单推导一下。

我们设定实验老虎机的回报满足伯努利分布（即1/0），每台摇臂获胜的概率为q，则输的概率是1-q。同时我们定义s 和 f 分别是之前以一系列实验中收集的该摇臂获胜和输钱的次数，这样我们关心的是每个摇臂下一次可能获胜的后验概率分布，即P(q|s,f)。在贝叶斯定理【13】中后验概率通过如下公式计算：

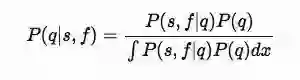
从这个公式中我们需要进一步计算P(s,f|q) 和 P(q)，其中 P(s,f|q)的含义是基于摇臂的胜率q，在s+f次实验中获胜s次的概率。这里我们可以用二项式分布【14】来计算一系列独立实验后获胜的次数，公式如下：

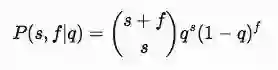
而另一部分P(q)代表与P(q|s,f)属于共轭分布【15】的先验分布，在伯努利分布中共轭先验分布是Beta 分布：

即

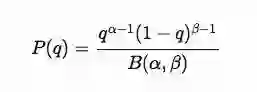
这里α,β代表胜率和失败率的大于0的参数， B是Beta分布中的正则化常量，以确保整体概率为1.

现在我们将这两部分整合到贝叶斯定理的公式中，经过推导得到下面的结果：

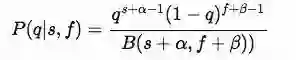
该结果从形式上是一个新的Bate分布，只是参数变成了α+s和β+f。这样通过Bate分布和目前的各摇臂的胜负次数，我们能计算出每个摇臂当前最好的获胜概率，从而选择下一步的行动。我们可以设定α=β=1，在没有先验知识的时候（s=f=0）相当于开始随机探索；胜负次数累积的越多，后验胜率就会评估的越准确。

在python实现【16】中，我们把三个摇臂当前的获胜次数(1+s)和失败次数（1+f）作为参数传入numpy.random.beta()方法中计算各摇臂的后验货胜率，然后选择当前胜率最大的摇臂去玩下一次。

def return_thompson_action(success_counter_array, failure_counter_array):
    """Return an action using Thompson sampling

    @param success_counter_array (alpha) success rate for each action
    @param failure_counter_array (beta) failure rate for each action
    @return the action selected
    """
    beta_sampling_array = np.random.beta(success_counter_array, 
                                         failure_counter_array)
    return np.argmax(beta_sampling_array)

测试的结果出奇的好：

Average cumulated reward: 791.21
Average utility distribution: [0.39188487  0.50654831  0.80154085]
Average utility RMSE: 0.0531917417346

▌小结

---

---

Tompson sampling策略的平均回报是目前策略中最好的，0.05的错误率在效用函数中算是相对低的。从目前的设定看Thompson应该是最好的策略。但是如果在更复杂的场景下，计算后验分布的复杂度也会相应增加。所以需要更全面的评估某一算法的应用。这里有更详细的Thompson Sampling的最新教程【17】，我会在接下来的文章中进行更深入的分析。

【1】https://en.wikipedia.org/wiki/Markov_decision_process

【2】https://github.com/XinyuYun/dissecting-reinforcement-learning/tree/master/src/6/multi-armed-bandit

【3】https://zh.wikipedia.org/wiki/伯努利分布

【4】https://zh.wikipedia.org/wiki/方均根差

【5】https://github.com/XinyuYun/dissecting-reinforcement-learning/blob/master/src/6/multi-armed-bandit/random_agent_bandit.py

【6】https://github.com/XinyuYun/dissecting-reinforcement-learning/blob/master/src/6/multi-armed-bandit/greedy_agent_bandit.py

【7】https://github.com/XinyuYun/dissecting-reinforcement-learning/blob/master/src/6/multi-armed-bandit/epsilon_greedy_agent_bandit.py

【8】https://zh.wikipedia.org/wiki/Softmax函数

【9】https://github.com/XinyuYun/dissecting-reinforcement-learning/blob/master/src/6/multi-armed-bandit/softmax_agent_bandit.py

【10】https://github.com/XinyuYun/dissecting-reinforcement-learning/blob/master/src/6/multi-armed-bandit/epsilon_decreasing_agent_bandit.py

【11】https://en.wikipedia.org/wiki/Thompson_sampling

【12】https://zh.wikipedia.org/wiki/最大似然估计

【13】https://zh.wikipedia.org/wiki/贝叶斯定理

【14】https://zh.wikipedia.org/wiki/二項分佈#伯努利分布

【15】https://en.wikipedia.org/wiki/Conjugate_prior

【16】https://github.com/XinyuYun/dissecting-reinforcement-learning/blob/master/src/6/multi-armed-bandit/thompson_agent_bandit.py

【17】https://arxiv.org/abs/1707.02038

参考文献

主体文章翻译和GitHub代码来自 Dissecting Reinforcement Learning Blog

https://mpatacchiola.github.io/blog/

作者GitHu XinyuYun/dissecting-reinforcement-learning

https://github.com/XinyuYun/dissecting-reinforcement-learning/tree/master/src/6/multi-armed-bandit

Thompson Sampling的最新教程 [1707.02038] A Tutorial on Thompson Sampling

https://arxiv.org/abs/1707.02038

来源：知乎 -StanleyFoo，专知已获得作者授权。

https://zhuanlan.zhihu.com/p/33837910

-END-

专 · 知

人工智能领域主题知识资料查看获取：【专知荟萃】人工智能领域26个主题知识资料全集（入门/进阶/论文/综述/视频/专家等）

请PC登录www.zhuanzhi.ai或者点击阅读原文，注册登录专知，获取更多AI知识资料！

请扫一扫如下二维码关注我们的公众号，获取人工智能的专业知识！

请加专知小助手微信（Rancho_Fang），加入专知主题人工智能群交流！加入专知主题群（请备注主题类型：AI、NLP、CV、 KG等）交流~

点击“阅读原文”，使用专知