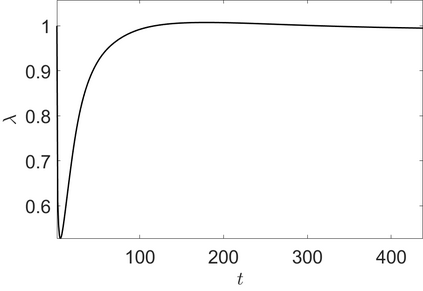
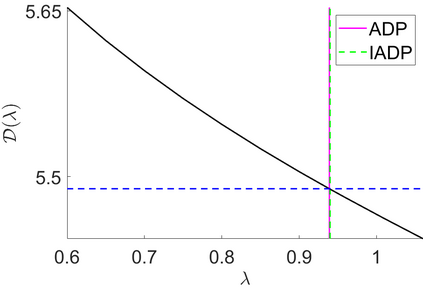
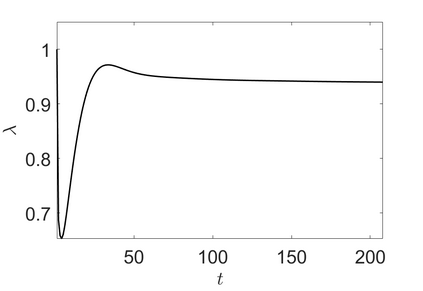
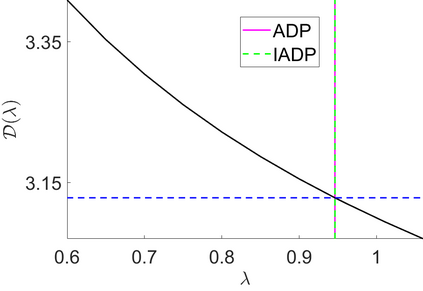
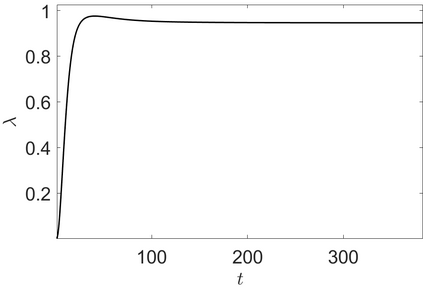
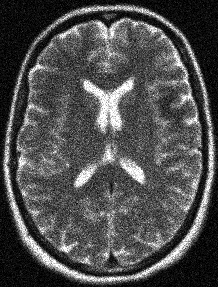
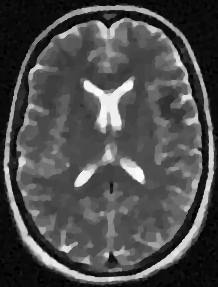
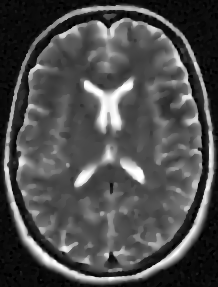
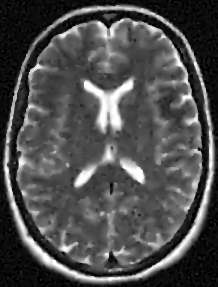
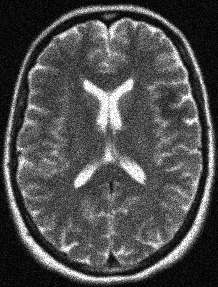
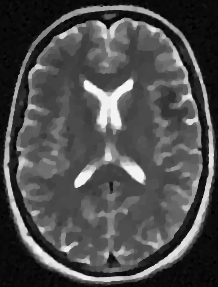
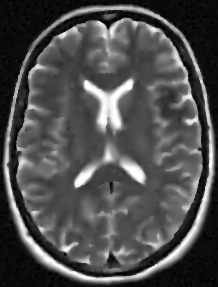
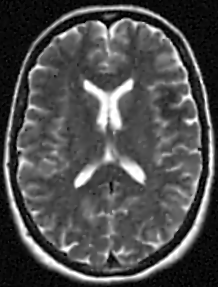
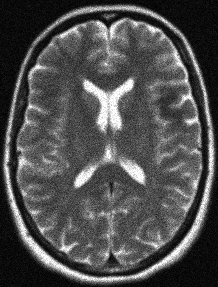
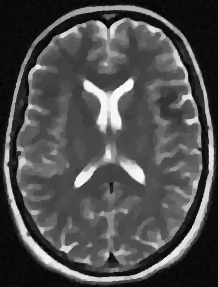
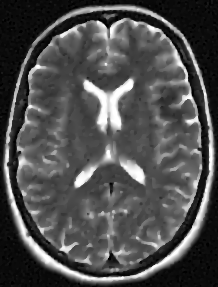
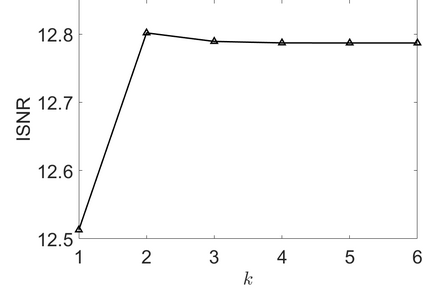
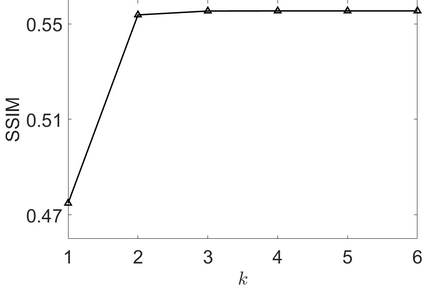
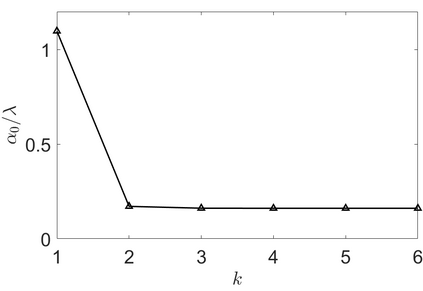
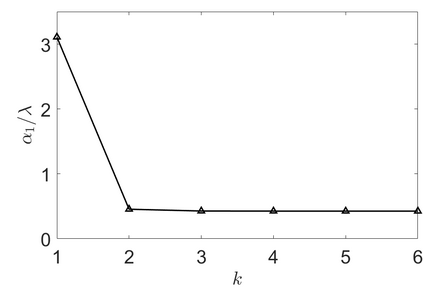
We address the image restoration problem under Poisson noise corruption. The Kullback-Leibler divergence, which is typically adopted in the variational framework as data fidelity term in this case, is coupled with the second-order Total Generalized Variation (TGV$^2$). The TGV$^2$ regularizer is known to be capable of preserving both smooth and piece-wise constant features in the image, however its behavior is subject to a suitable setting of the parameters arising in its expression. We propose a hierarchical Bayesian formulation of the original problem coupled with a Maximum A Posteriori estimation approach, according to which the unknown image and parameters can be jointly and automatically estimated by minimizing a given cost functional. The minimization problem is tackled via a scheme based on the Alternating Direction Method of Multipliers, which also incorporates a procedure for the automatic selection of the regularization parameter by means of a popular discrepancy principle. Computational results show the effectiveness of our proposal.
翻译:我们处理Poisson噪音腐败中的图像恢复问题。 Kullback- Leibler 差异通常在变异框架中作为数据忠诚术语在本案中被采用,与第二阶总通用变换(TGV$$2美元)相配合。据了解,TGV$2$的正规化器能够保存图像中的光滑和片断常态特征,但其行为取决于其表达方式中产生的参数的适当设置。我们建议对原始问题采用一种等级分级的Bayesian 公式,同时采用最高后验估计方法,根据这种方法,未知的图像和参数可以通过尽量减少特定成本功能来联合和自动估算。最小化问题通过基于多动器变换方向法的办法加以解决,该办法还包含一个程序,通过流行差异原则自动选择规范参数。计算结果显示我们提案的有效性。