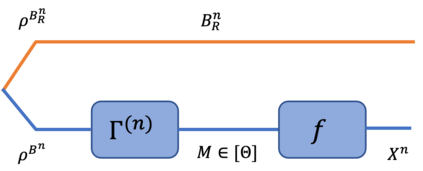
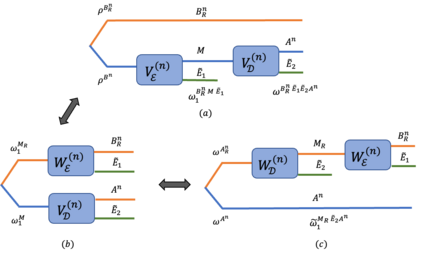
We consider the lossy quantum source coding problem where the task is to compress a given quantum source below its von Neumann entropy. Inspired by the duality connections between the rate-distortion and channel coding problems in the classical setting, we propose a new formulation for the lossy quantum source coding problem. This formulation differs from the existing quantum rate-distortion theory in two aspects. Firstly, we require that the reconstruction of the compressed quantum source fulfill a global error constraint as opposed to the sample-wise local error criterion used in the standard rate-distortion setting. Secondly, instead of a distortion observable, we employ the notion of a backward quantum channel, which we refer to as a "posterior reference map", to measure the reconstruction error. Using these, we characterize the asymptotic performance limit of the lossy quantum source coding problem in terms of single-letter coherent information of the given posterior reference map. We demonstrate a protocol to encode (at the specified rate) and decode, with the reconstruction satisfying the provided global error criterion, and therefore achieving the asymptotic performance limit. The protocol is constructed by decomposing coherent information as a difference of two Holevo information quantities, inspired from prior works in quantum communication problems. To further support the findings, we develop analogous formulations for the quantum-classical and classical variants and express the asymptotic performance limit in terms of single-letter mutual information quantities with respect to appropriately defined channels analogous to posterior reference maps. We also provide various examples for the three formulations, and shed light on their connection to the standard rate-distortion formulation wherever possible.
翻译:我们考虑的是损失量源编码问题, 任务在于将给定量源压缩到 von Neumann entropy 下方的量源中。 在古典环境中, 率扭曲和频道编码问题之间的双重联系启发下, 我们为损失量源编码问题提出新的配方。 这个配方与现有的量量子调制理论在两个方面不同。 首先, 我们要求压缩量源的重建要达到全球错误限制, 而不是标准调制设置中使用的样本式地方错误标准。 其次, 我们使用一个后向量数据频道的概念, 我们称之为“前置参考地图”, 来测量重建错误。 我们用这些词来描述损失量源编码问题, 单字母一致的调和调和调和调, 我们用一个协议来编码( 特定速率 ), 并且根据所提供的全球误差标准, 从而实现“ 度” 缩略图的连接 。 协议是, 将 校正级 数据 定义 的 格式, 以 校正 的 格式 格式 定义 格式 定义 格式, 定义 格式 格式 定义 格式 格式 定义 格式 的 格式, 定义 定义 格式 格式 格式 的 的, 定义 格式 定义 格式 格式 格式 的,, 定义 定义 格式 格式 格式,, 定义 格式 格式 格式 格式,,,, 定义 格式 格式 格式 格式,, 格式,,,, 格式 格式,, 定义 定义, 定义 定义 定义 格式,, 定义 定义,,,, 定义 定义,,,,,,,,, 定义,,,,,,, 定义 定义,,, 定义 定义 定义 定义 定义,,, 定义 定义,,,,, 定义 定义 定义 定义, 定义,,,,,, 定义 定义 定义 定义, 定义