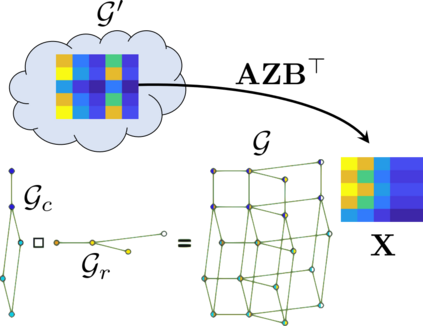
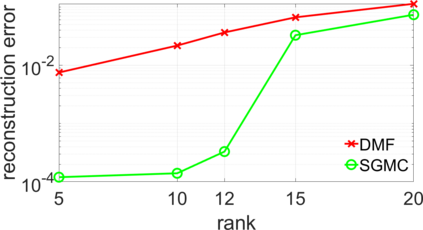
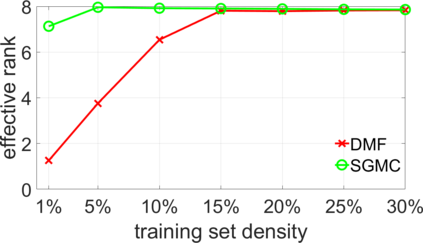
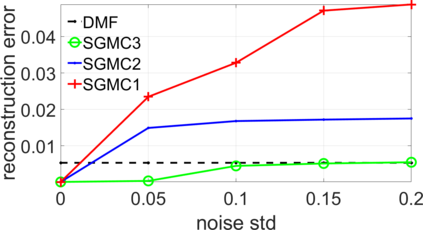
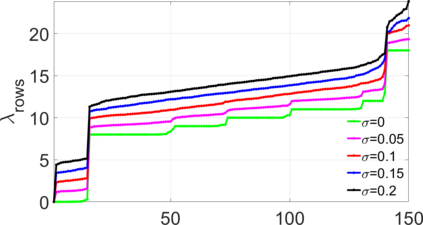
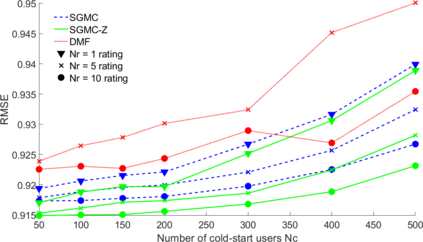
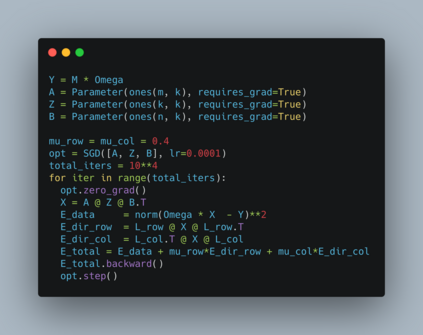
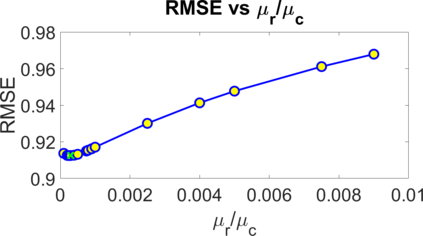
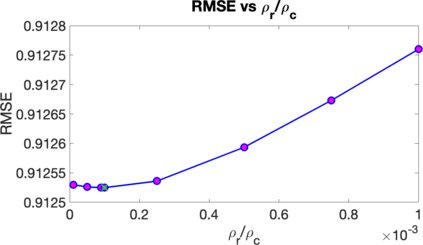
Deep Matrix Factorization (DMF) is an emerging approach to the problem of matrix completion. Recent works have established that gradient descent applied to a DMF model induces an implicit regularization on the rank of the recovered matrix. In this work we interpret the DMF model through the lens of spectral geometry. This allows us to incorporate explicit regularization without breaking the DMF structure, thus enjoying the best of both worlds. In particular, we focus on matrix completion problems with underlying geometric or topological relations between the rows and/or columns. Such relations are prevalent in matrix completion problems that arise in many applications, such as recommender systems and drug-target interaction. Our contributions enable DMF models to exploit these relations, and make them competitive on real benchmarks, while exhibiting one of the first successful applications of deep linear networks.
翻译:深母体因子化(DMF)是解决矩阵完成问题的一种新办法,最近的工作已经确定,在DMF模式中,梯度下降会导致对回收的矩阵的等级进行隐含的正规化;在这项工作中,我们通过光谱几何学透镜来解释DMF模式;这使我们能够在不打破DMF结构的情况下纳入明确的正规化,从而享受两个世界的最佳条件;特别是,我们侧重于行和(或)列之间基本的几何或地貌关系中的矩阵完成问题;这种关系在许多应用中出现的矩阵完成问题中普遍存在,例如推荐系统和药物目标互动。我们的贡献使得DMF模式能够利用这些关系,使它们在实际基准上具有竞争力,同时展示深线网络的首批成功应用之一。