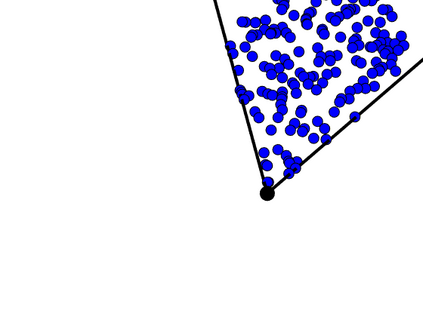
Mixed membership community detection is a challenge problem in network analysis. To estimate the memberships and study the impact of regularized spectral clustering under the mixed membership stochastic block (MMSB) model, this article proposes two efficient spectral clustering approaches based on regularized Laplacian matrix, Simplex Regularized Spectral Clustering (SRSC) and Cone Regularized Spectral Clustering (CRSC). SRSC and CRSC methods are designed based on the ideal simplex structure and the ideal cone structure in the variants of the eigen-decomposition of the population regularized Laplacian matrix. We show that these two approaches SRSC and CRSC are asymptotically consistent under mild conditions by providing error bounds for the inferred membership vector of each node under MMSB. Through the theoretical analysis, we give the upper and lower bound for the regularizer $\tau$. By introducing a parametric convergence probability, we can directly see that when $\tau$ is large these two methods may still have low error rates but with a smaller probability. Thus we give an empirical optimal choice of $\tau$ is $O(log(n))$ with $n$ the number of nodes to detect sparse networks. The proposed two approaches are successfully applied to synthetic and empirical networks with encouraging results compared with some benchmark methods.
翻译:在网络分析中,对混合成员群进行检测是一个难题。为了估计成员和研究混合成员区块模型(MMSB)下常规光谱聚集的影响,本条款提出两种高效的光谱聚集方法,其基础是固定的拉普拉西亚矩阵、简易的常规光谱聚集(SRSC)和Cone 常规的光谱聚集(CRSC)。SRSC和CRCSC方法的设计基于理想的简单结构以及人口分解变模型中的理想锥形结构。我们发现,在混合成员区块模型(MMSB)模型中,这两种方法在固定化的拉普拉普拉西亚矩阵(MMSB)矩阵、简单化的光谱质聚集(SICB)和Cone 常规化的光谱聚集(COSC)。通过理论分析,我们给正规化聚集体的上下层和下层聚集集体(CRCSC)设定了上限。通过引入一个分数的趋同概率,我们直接看到,当美元这两种方法巨大时,可能仍然有低的错误率,但概率较小。因此,SRSC和CSC在较轻的条件下,我们用美元模拟网络进行实验性最佳选择。我们用美元测试后,用美元测试后,用美元测试后,对数字的模型检测。