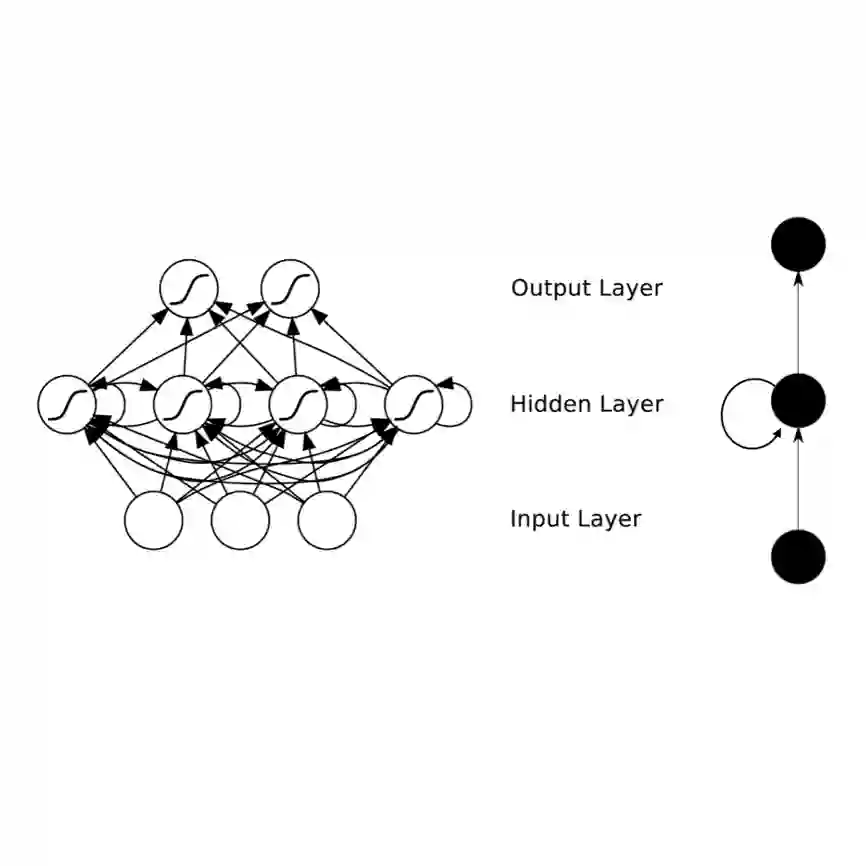
The Fisher information metric is an important foundation of information geometry, wherein it allows us to approximate the local geometry of a probability distribution. Recurrent neural networks such as the Sequence-to-Sequence (Seq2Seq) networks that have lately been used to yield state-of-the-art performance on speech translation or image captioning have so far ignored the geometry of the latent embedding, that they iteratively learn. We propose the information geometric Seq2Seq (GeoSeq2Seq) network which abridges the gap between deep recurrent neural networks and information geometry. Specifically, the latent embedding offered by a recurrent network is encoded as a Fisher kernel of a parametric Gaussian Mixture Model, a formalism common in computer vision. We utilise such a network to predict the shortest routes between two nodes of a graph by learning the adjacency matrix using the GeoSeq2Seq formalism; our results show that for such a problem the probabilistic representation of the latent embedding supersedes the non-probabilistic embedding by 10-15\%.
翻译:渔业信息衡量标准是信息几何的重要基础,它使我们得以近似概率分布的局部几何。经常神经网络,例如最近用来产生语音翻译或图像字幕最新性能的序列到序列(Seq2Seqeq)网络,迄今为止忽视了潜嵌入的几何,而它们反复学习了潜嵌入。我们提议了Seq2Seqeq(GeoSeq2Seqeq)网络,它缩小了深层经常性神经网络与信息几何之间的差距。具体地说,经常网络提供的潜嵌入网络被编码为高斯断层模型的渔业内核,这是计算机愿景中常见的一种形式主义。我们利用这样一个网络,通过使用地理Seq2Seqeg正式主义学习相邻矩阵来预测图的两个节点之间的最短路径;我们的结果显示,在出现这一问题时,潜嵌入的概率代表率代表取代了10-15年前的非不稳定嵌入。