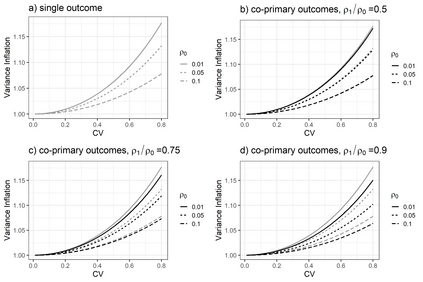
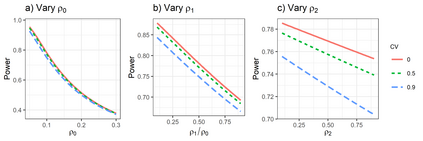
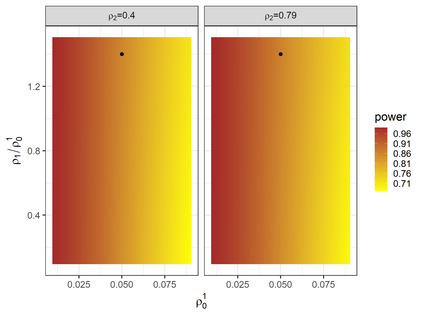
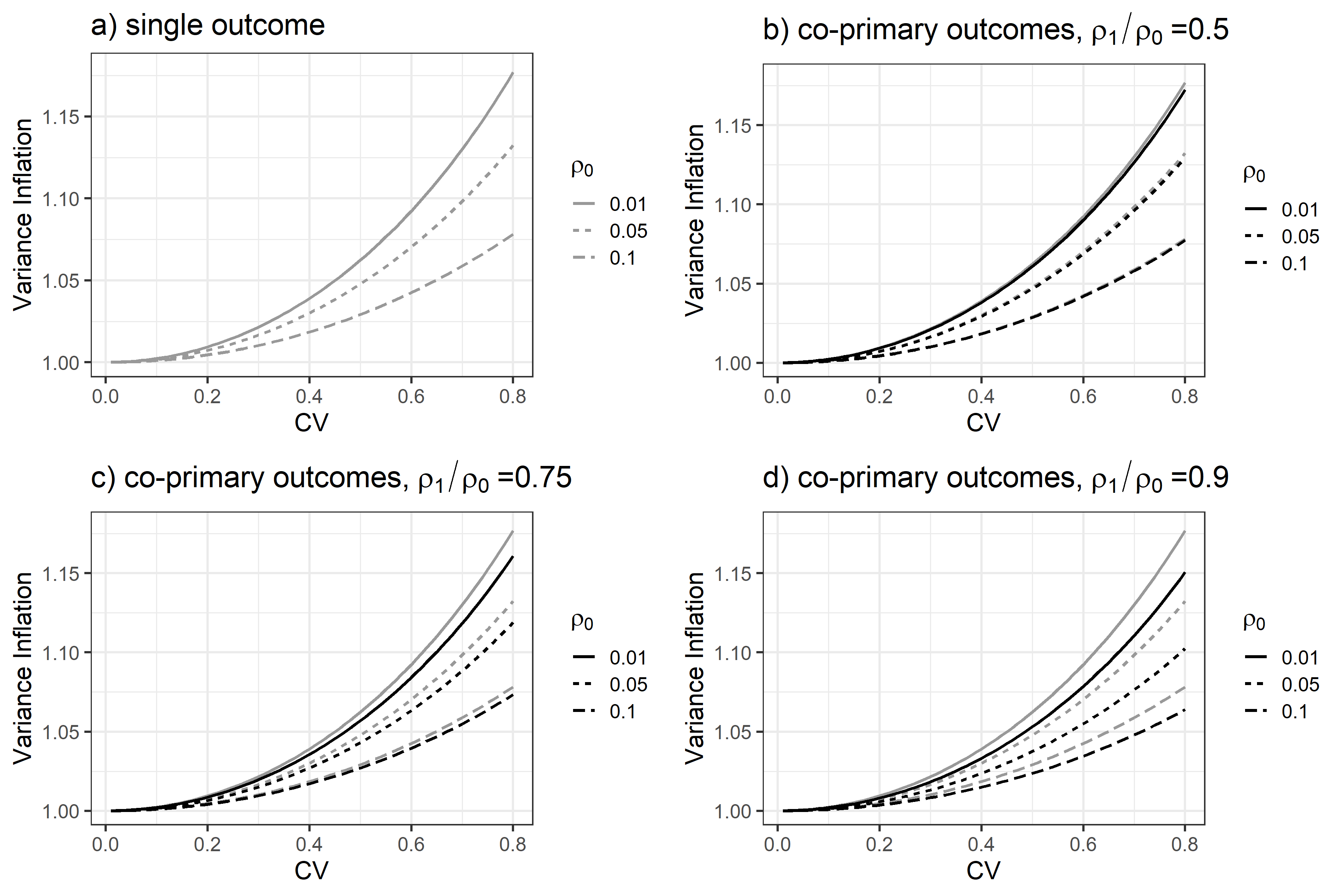
Pragmatic trials evaluating health care interventions often adopt cluster randomization due to scientific or logistical considerations. Previous reviews have shown that co-primary endpoints are common in pragmatic trials but infrequently recognized in sample size or power calculations. While methods for power analysis based on $K$ ($K\geq 2$) binary co-primary endpoints are available for CRTs, to our knowledge, methods for continuous co-primary endpoints are not yet available. Assuming a multivariate linear mixed model that accounts for multiple types of intraclass correlation coefficients (endpoint-specific ICCs, intra-subject ICCs and inter-subject between-endpoint ICCs) among the observations in each cluster, we derive the closed-form joint distribution of $K$ treatment effect estimators to facilitate sample size and power determination with different types of null hypotheses under equal cluster sizes. We characterize the relationship between the power of each test and different types of correlation parameters. We further relax the equal cluster size assumption and approximate the joint distribution of the $K$ treatment effect estimators through the mean and coefficient of variation of cluster sizes. Our simulation studies with a finite number of clusters indicate that the predicted power by our method agrees well with the empirical power, when the parameters in the multivariate linear mixed model are estimated via the expectation-maximization algorithm. An application to a real CRT is presented to illustrate the proposed method.
翻译:由于科学或后勤方面的考虑,评估保健干预措施的简单试验往往采用集束随机化。以前的审查表明,在务实试验中,共同初级终点是常见的,但在抽样规模或电量计算中并不经常承认。虽然CRT可以使用基于K$(K\geq 2美元)的二元共同初级终点分析方法,但据我们所知,目前还没有关于连续共同初级终点的方法。假设一种多变量线性线性混合模型,在每组观察中考虑到多种类型的类内相关系数(特定点的电算中心、本体内电算中心和端点间电算中心之间),但我们得出了美元治疗效应的封闭式联合分布,估计值是K$(K$)的治疗效应,以便利在相同组内规模下不同种类的空虚假设确定。我们用每种类型的无理假设值确定每组的能量规模和不同类型相关参数之间的关系。我们进一步放松了对等值的集群规模假设,并估计美元待遇效应通过组合体大小的平均值和系数进行联合分配。我们通过组合体积规模的预测的模型中的一种模拟研究与估计法方法一致地表明了我们预测的数值。