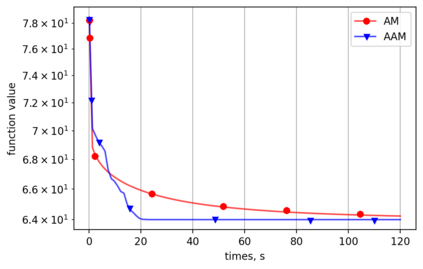
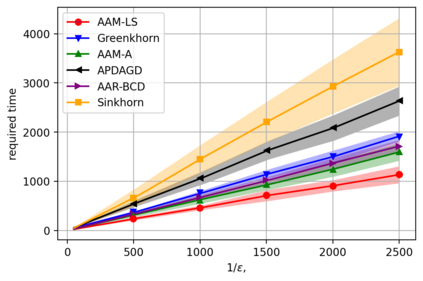
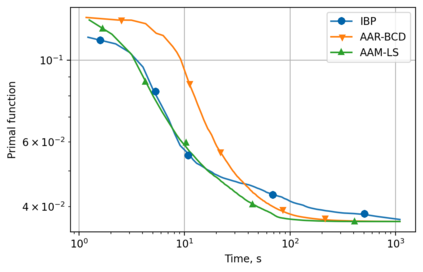
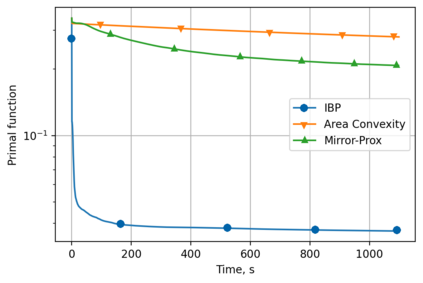
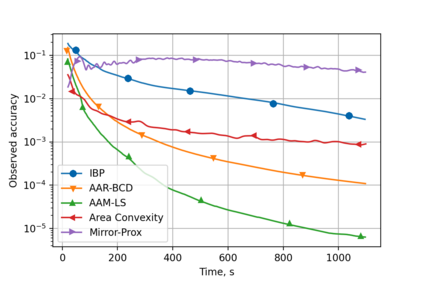
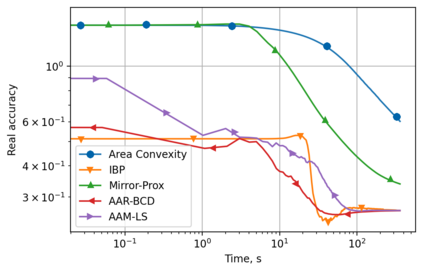
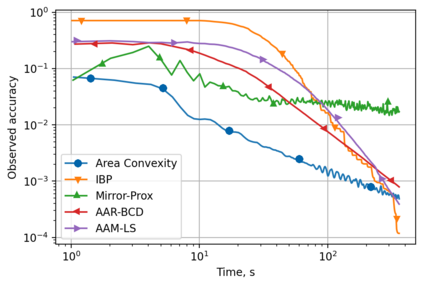
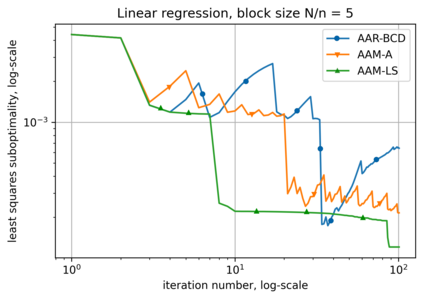
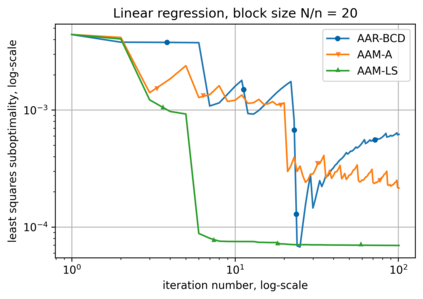
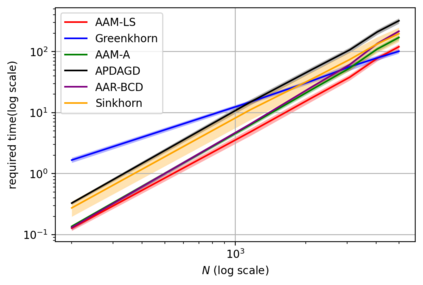
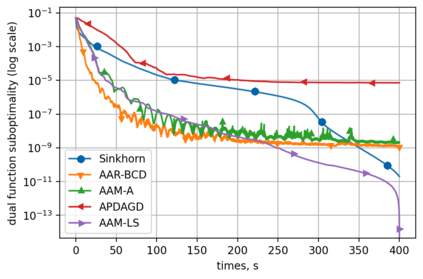
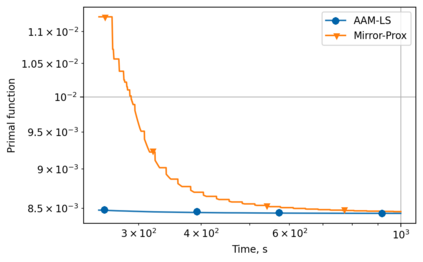
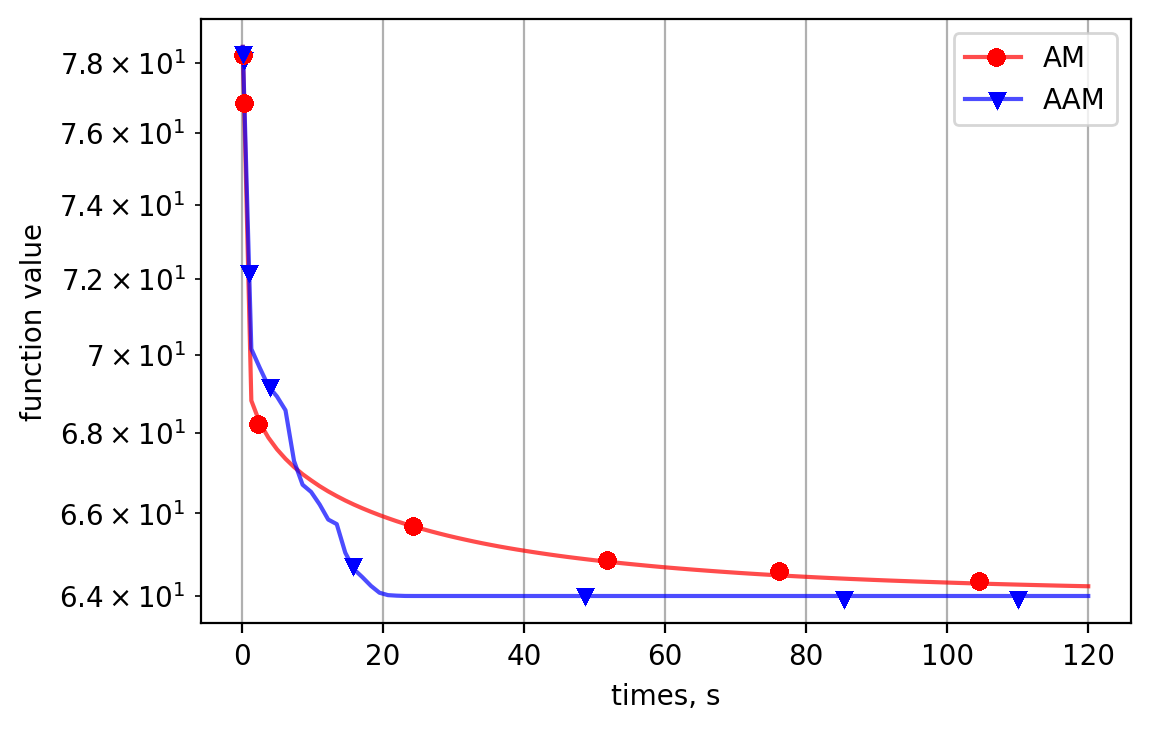
Alternating minimization (AM) procedures are practically efficient in many applications for solving convex and non-convex optimization problems. On the other hand, Nesterov's accelerated gradient is theoretically optimal first-order method for convex optimization. In this paper we combine AM and Nesterov's acceleration to propose an accelerated alternating minimization algorithm. We prove $1/k^2$ convergence rate in terms of the objective for convex problems and $1/k$ in terms of the squared gradient norm for non-convex problems, where $k$ is the iteration counter. Our method does not require any knowledge of neither convexity of the problem nor function parameters such as Lipschitz constant of the gradient, i.e. it is adaptive to convexity and smoothness and is uniformly optimal for smooth convex and non-convex problems. Further, we develop its primal-dual modification for strongly convex problems with linear constraints and prove the same $1/k^2$ for the primal objective residual and constraints feasibility.
翻译:另一方面,Nesterov的加速梯度在理论上是最佳的调子优化第一阶方法。在本文件中,我们将AM和Nesterov的加速度结合起来,以提出加速交替最小化算法。我们证明,就结子问题的目标而言,1美元/k ⁇ 2美元的趋同率,就非结子问题而言,1美元/k$的平方梯度标准而言,对于非结子问题来说,1美元/k$是循环反差。我们的方法并不要求知道问题是否稳妥,也不要求知道功能参数,例如梯度的利普西茨常数,即它适应混凝度和光滑度,对于顺利的结子和非结子问题是统一的最佳办法。此外,我们为具有线性制约的强烈结子问题制定了原始调整法,并证明原始目标剩余和制约的可行性为1/k ⁇ 2美元。