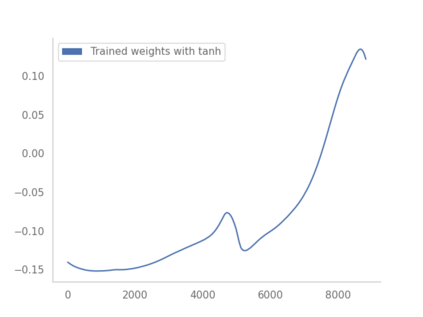
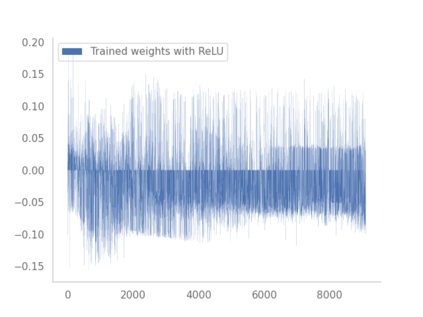
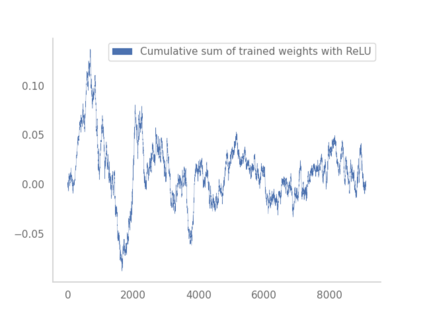
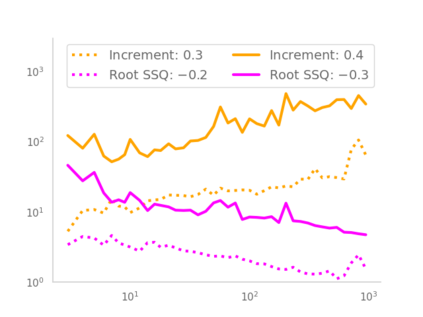
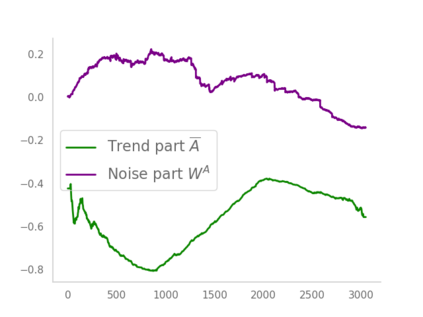
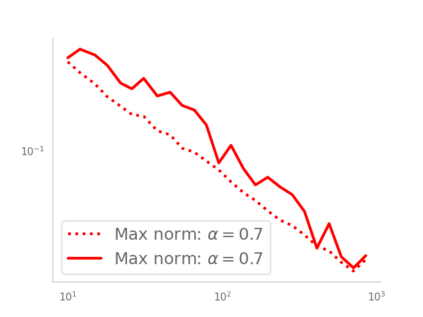
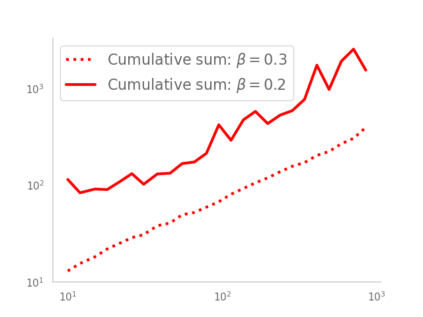
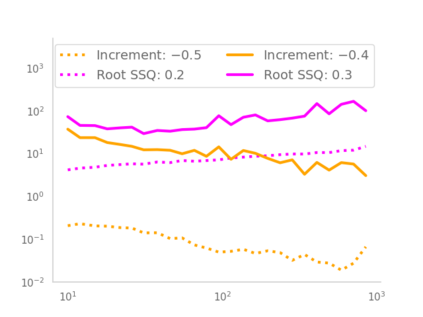
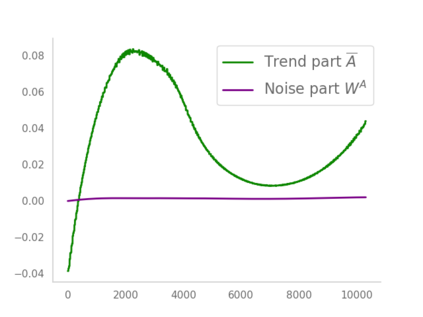
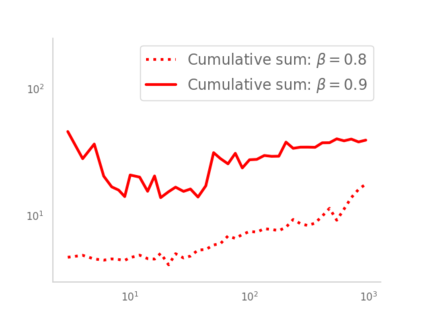
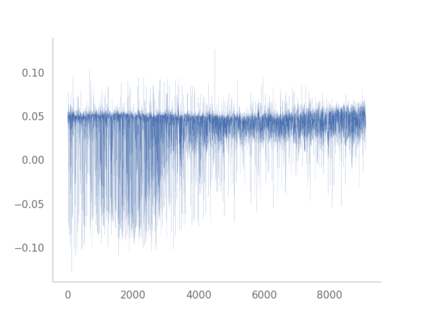
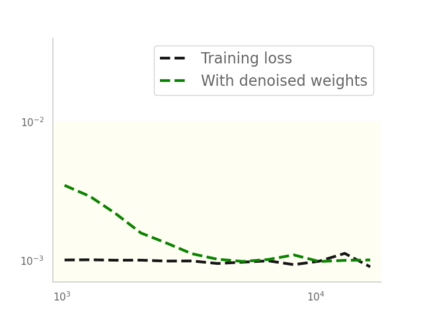
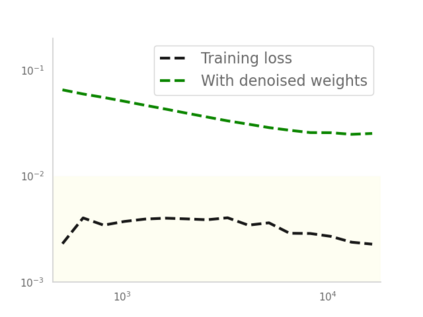
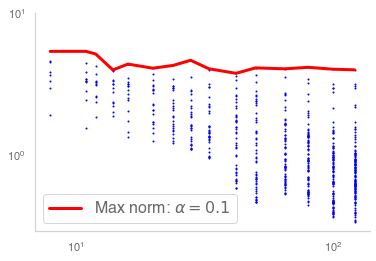
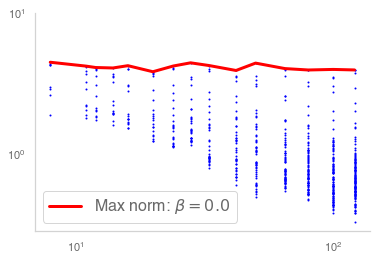
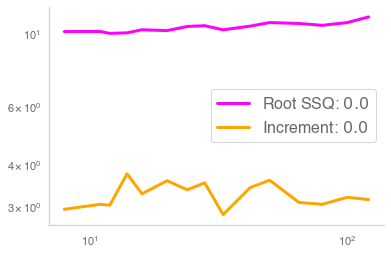
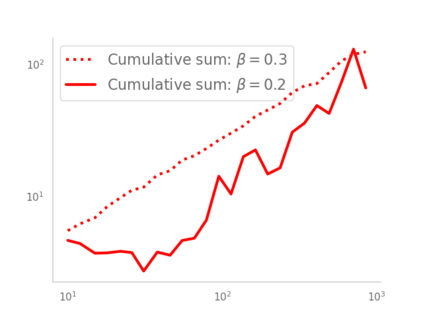
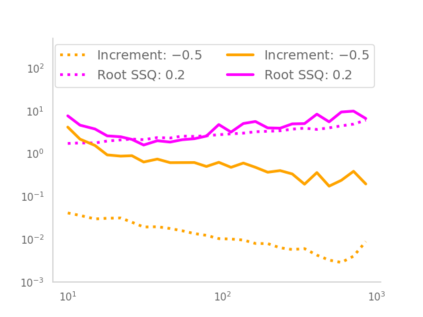
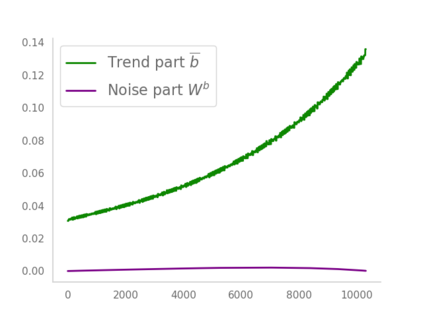
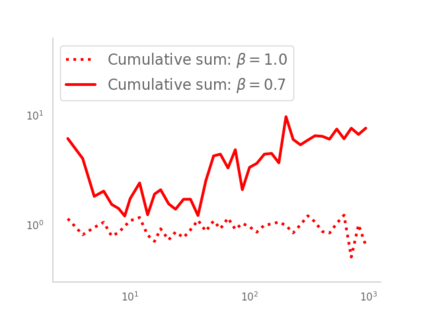
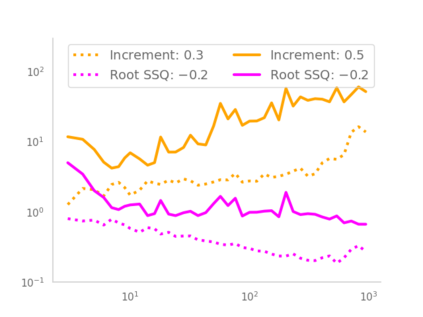
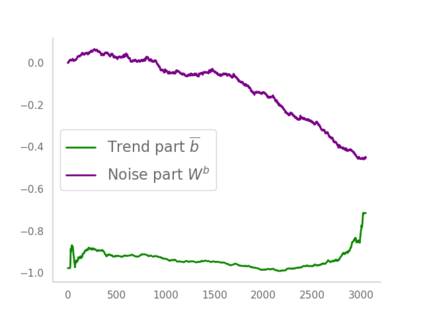
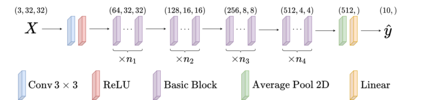
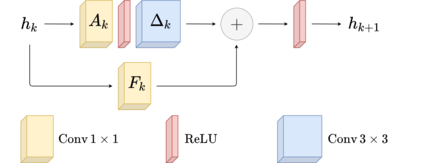
Residual networks (ResNets) have displayed impressive results in pattern recognition and, recently, have garnered considerable theoretical interest due to a perceived link with neural ordinary differential equations (neural ODEs). This link relies on the convergence of network weights to a smooth function as the number of layers increases. We investigate the properties of weights trained by stochastic gradient descent and their scaling with network depth through detailed numerical experiments. We observe the existence of scaling regimes markedly different from those assumed in neural ODE literature. Depending on certain features of the network architecture, such as the smoothness of the activation function, one may obtain an alternative ODE limit, a stochastic differential equation or neither of these. These findings cast doubts on the validity of the neural ODE model as an adequate asymptotic description of deep ResNets and point to an alternative class of differential equations as a better description of the deep network limit.
翻译:残余网络(ResNets)在模式识别方面表现出了令人印象深刻的结果,最近由于与神经普通差异方程式(神经普通数方程式)的明显联系,在理论上引起了相当大的兴趣。这种联系取决于网络重量的趋同,随着层数的增加而顺利发挥作用。我们通过详细的数字实验调查通过随机梯度梯度梯度梯度梯度下降所训练的重量的特性及其与网络深度的扩大。我们观察到存在着与神经代码文献中假设的显著不同的比例化制度。根据网络结构的某些特点,例如激活功能的顺利性,人们可以获得替代的 ODE 限值、 随机差异方程式等。这些结果使人怀疑神经代码模型作为深ResNet的适当的非象征性描述的有效性,并指明不同方程式的替代类别,以更好地描述深网络限值。