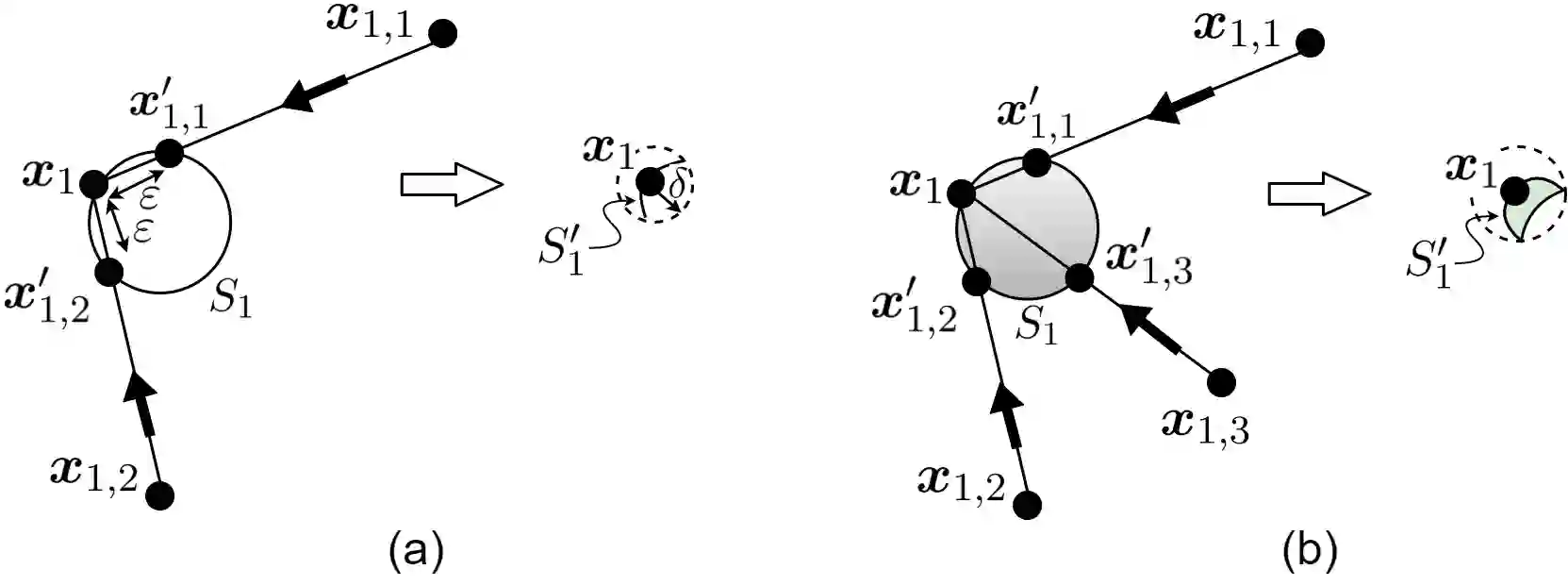
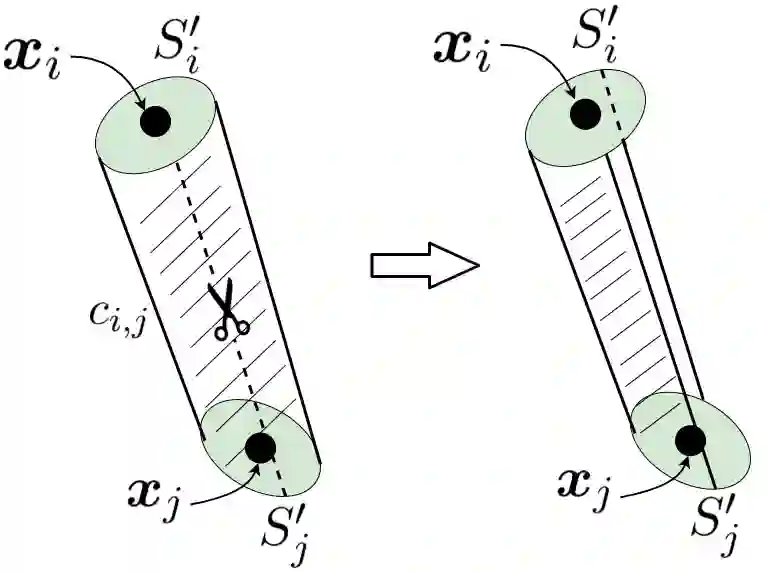
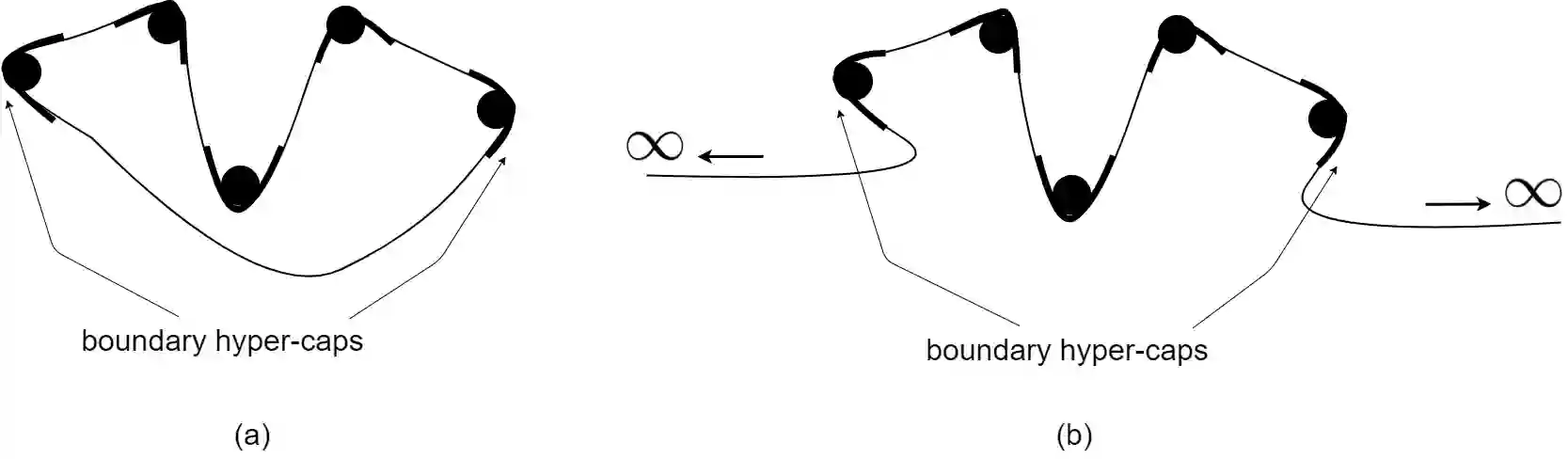
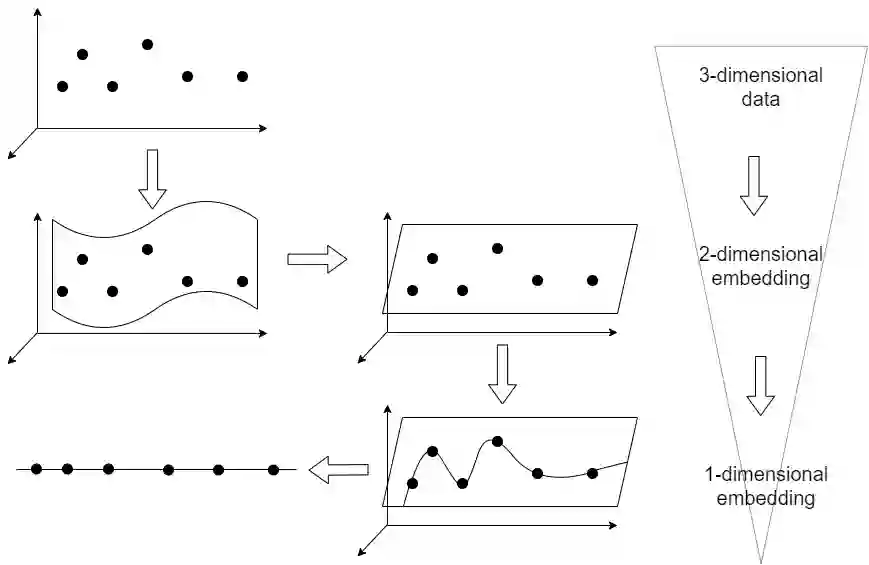
Consider a set of $n$ data points in the Euclidean space $\mathbb{R}^d$. This set is called dataset in machine learning and data science. Manifold hypothesis states that the dataset lies on a low-dimensional submanifold with high probability. All dimensionality reduction and manifold learning methods have the assumption of manifold hypothesis. In this paper, we show that the dataset lies on an embedded hypersurface submanifold which is locally $(d-1)$-dimensional. Hence, we show that the manifold hypothesis holds at least for the embedding dimensionality $d-1$. Using an induction in a pyramid structure, we also extend the embedding dimensionality to lower embedding dimensionalities to show the validity of manifold hypothesis for embedding dimensionalities $\{1, 2, \dots, d-1\}$. For embedding the hypersurface, we first construct the $d$ nearest neighbors graph for data. For every point, we fit an osculating hypersphere $S^{d-1}$ using its neighbors where this hypersphere is osculating to a hypothetical hypersurface. Then, using surgery theory, we apply surgery on the osculating hyperspheres to obtain $n$ hyper-caps. We connect the hyper-caps to one another using partial hyper-cylinders. By connecting all parts, the embedded hypersurface is obtained as the disjoint union of these elements. We discuss the geometrical characteristics of the embedded hypersurface, such as having boundary, its topology, smoothness, boundedness, orientability, compactness, and injectivity. Some discussion are also provided for the linearity and structure of data. This paper is the intersection of several fields of science including machine learning, differential geometry, and algebraic topology.
翻译:在 Euclidean 空间中考虑一套美元的数据点 $\ mathb{R ⁇ d$ 。 这组数据点被称为机器学习和数据科学中的数据集。 Manitlock 假设显示, 数据集位于低维次元值上, 概率高。 所有维度减少和多重学习方法都有多重假设的假设。 在本文中, 我们显示该数据集位于嵌入的超表层子值上, 这是本地的$( d-1) 维度。 因此, 我们显示, 多重假设至少对于嵌入的维度 $d-1$ 而言, 。 在机器结构中, 我们也可以将嵌入的基底度特性扩大到更低的维度, 以显示嵌入维度 $1, 2,\ dots, d-1 $。 对于嵌入超表层, 我们首先构建一个高基质的近邻系 。 我们使用其近端的超正深层正值, 以 = d= 1 。 我们使用此超深层的直径直径的直径直径直线值, 将部分的直径直径直系数据转换为超高空, 。