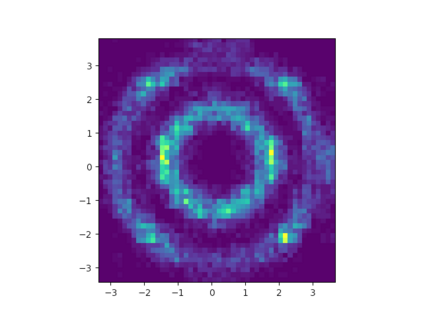
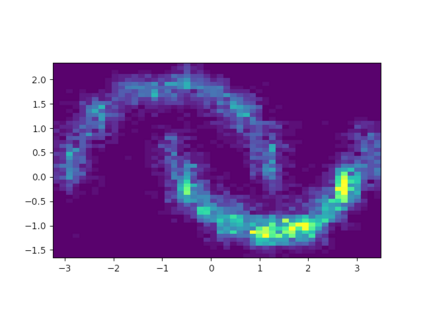
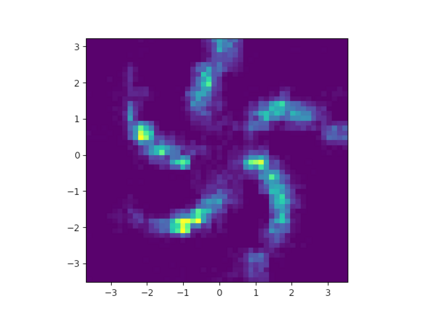
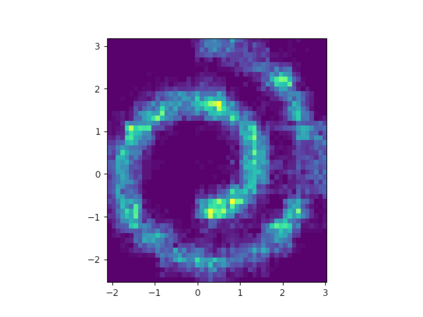
Learning the multivariate distribution of data is a core challenge in statistics and machine learning. Traditional methods aim for the probability density function (PDF) and are limited by the curse of dimensionality. Modern neural methods are mostly based on black-box models, lacking identifiability guarantees. In this work, we aim to learn multivariate cumulative distribution functions (CDFs), as they can handle mixed random variables, allow efficient box probability evaluation, and have the potential to overcome local sample scarcity owing to their cumulative nature. We show that any grid sampled version of a joint CDF of mixed random variables admits a universal representation as a naive Bayes model via the Canonical Polyadic (tensor-rank) decomposition. By introducing a low-rank model, either directly in the raw data domain, or indirectly in a transformed (Copula) domain, the resulting model affords efficient sampling, closed form inference and uncertainty quantification, and comes with uniqueness guarantees under relatively mild conditions. We demonstrate the superior performance of the proposed model in several synthetic and real datasets and applications including regression, sampling and data imputation. Interestingly, our experiments with real data show that it is possible to obtain better density/mass estimates indirectly via a low-rank CDF model, than a low-rank PDF/PMF model.
翻译:在统计和机器学习中,学习数据多变分布是一个核心挑战。传统方法针对概率密度函数(PDF),并受到维度诅咒的限制。现代神经方法大多以黑盒模型为基础,缺乏可识别性保障。在这项工作中,我们的目标是学习多变累积分布功能(CDF),因为它们可以处理混合随机变量,允许高效的箱概率评估,并有可能克服地方样本的累积性稀缺。我们表明,混合随机变量联合 CDF的任何网格抽样版本都通过Canonical Policadic(10or-rank)分解定位作为天真贝斯模型。通过引入低级模型,或者直接在原始数据领域,或者间接在转型的(Copula)领域,由此形成的模型可以提供高效的抽样、封闭形式的推断和不确定性量化,并在相对温和的条件下带来独特性保证。我们展示了拟议模型在几个合成和真实的数据集和应用中的优异性表现,包括回归、取样和数据内嵌入。有趣的是,我们通过低密度的实验可以间接地显示,我们的低密度数据模型。