On the numerical approximation of Blaschke-Santaló diagrams using Centroidal Voronoi Tessellations

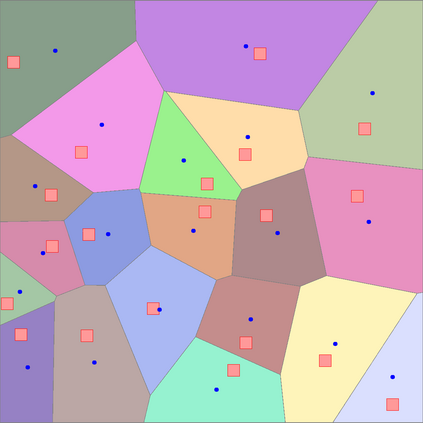
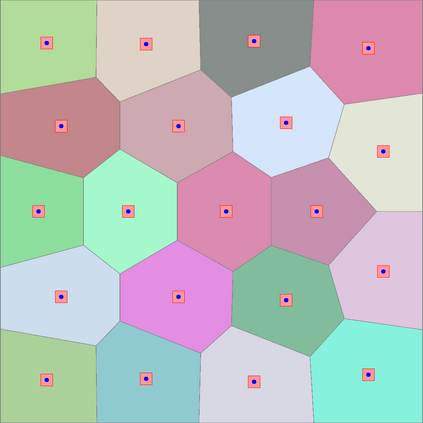
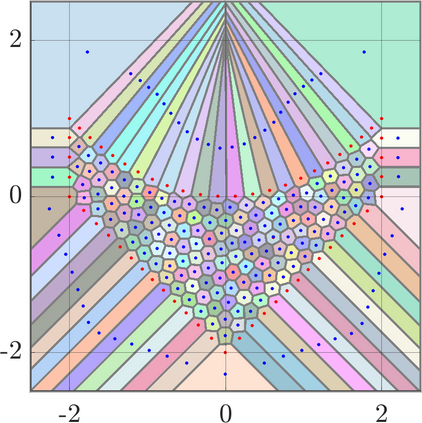
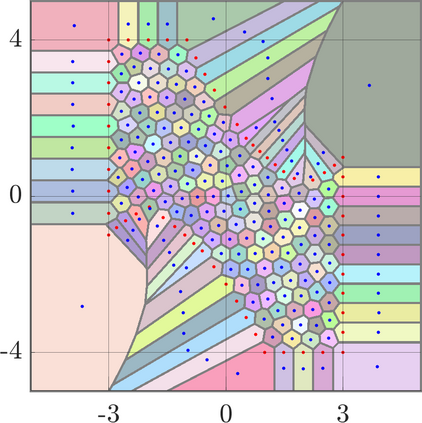
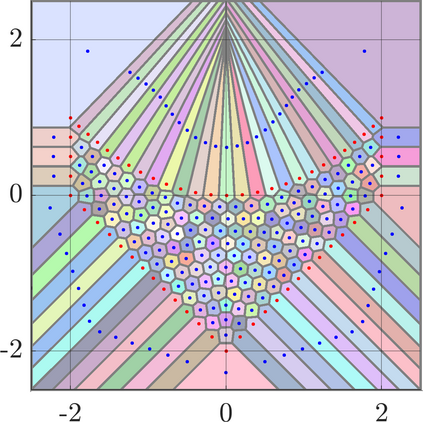
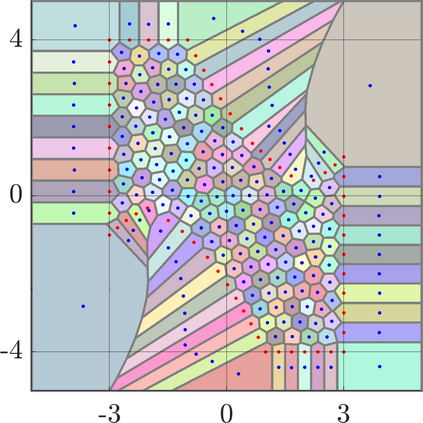
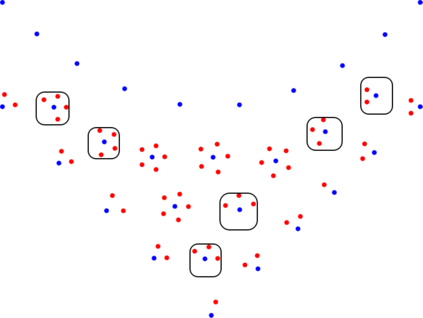
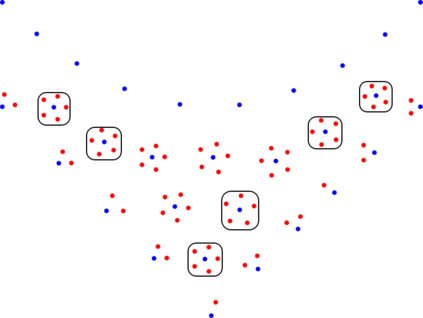
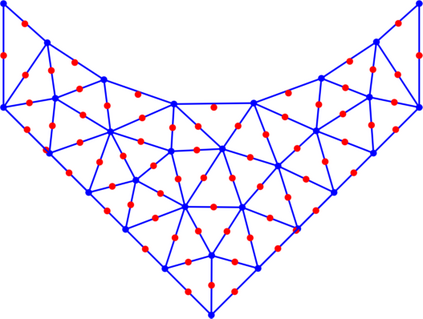
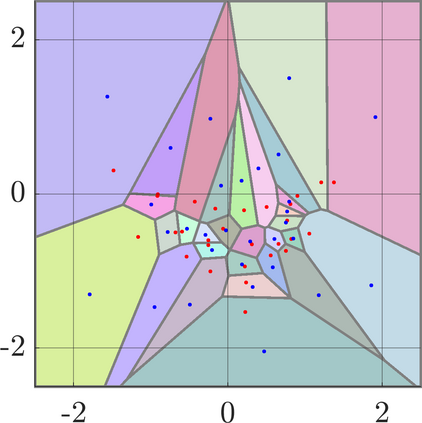
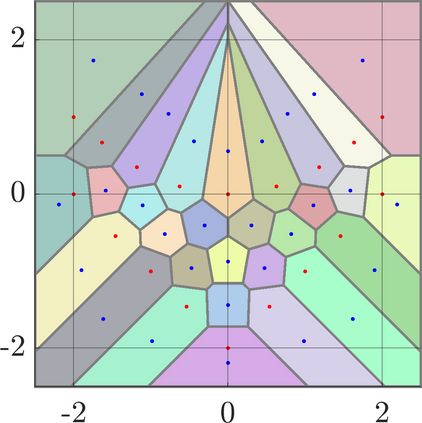
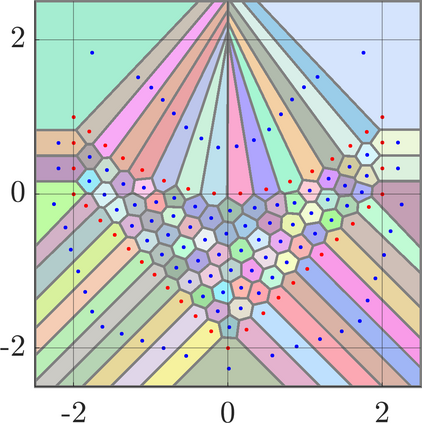
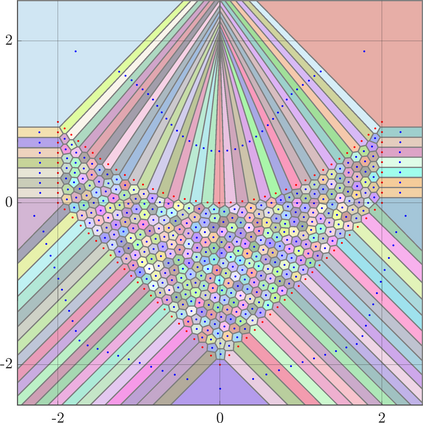
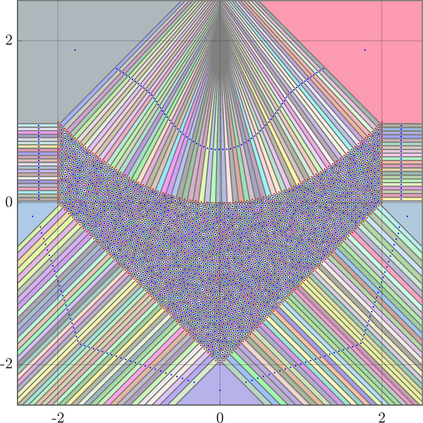
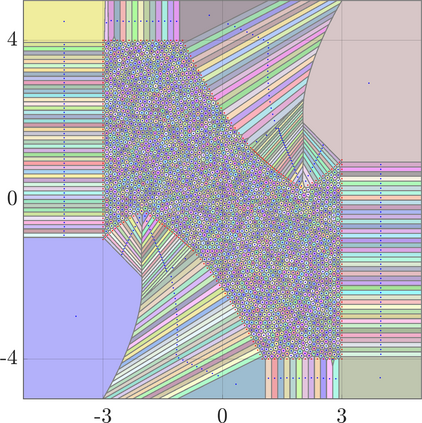
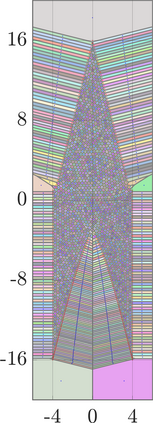
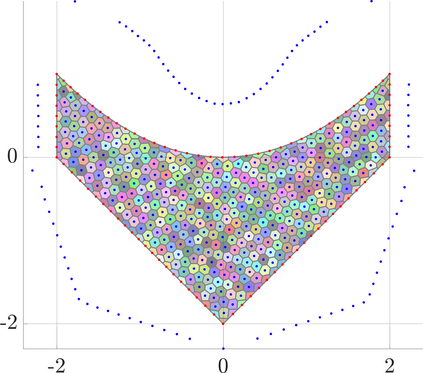
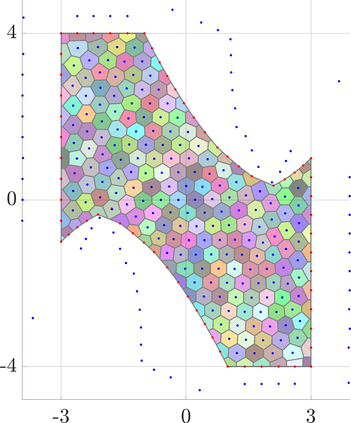
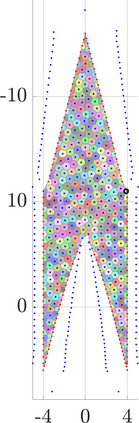
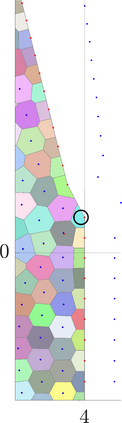
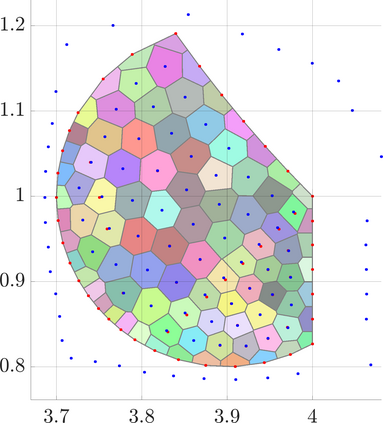
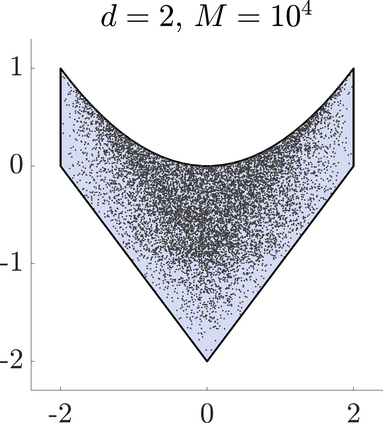
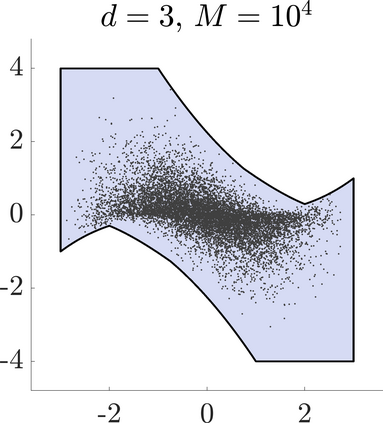
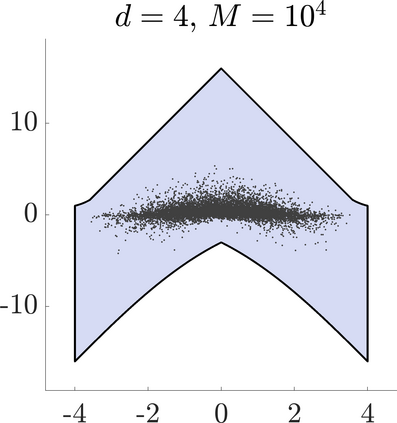
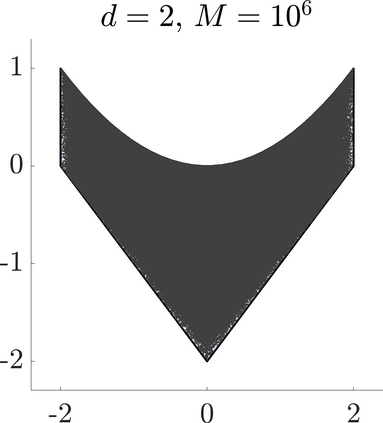
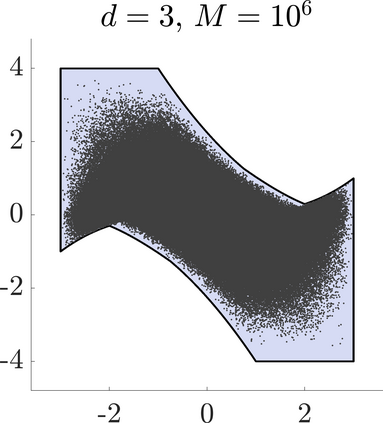
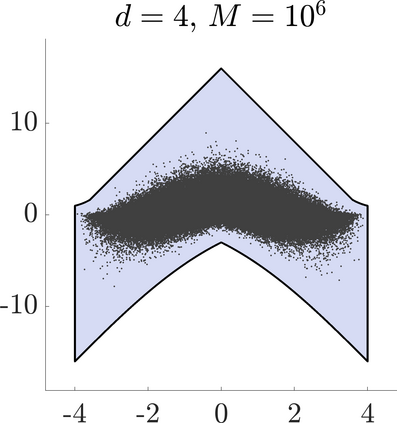
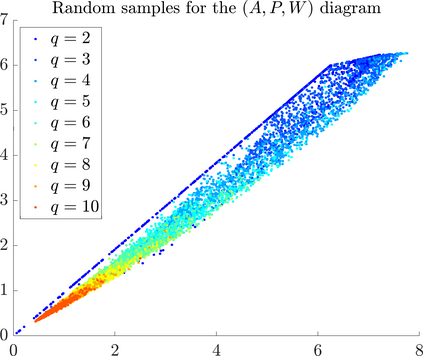
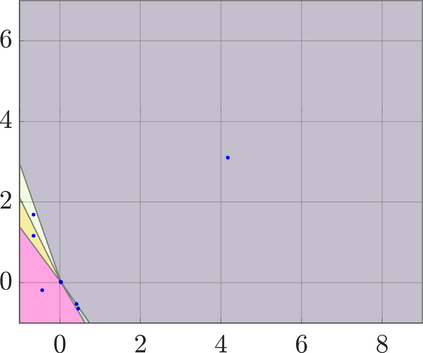
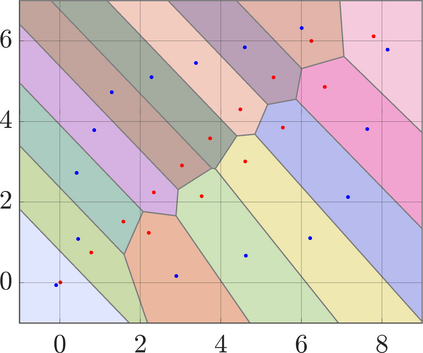
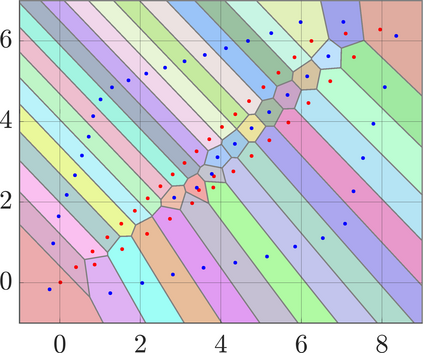
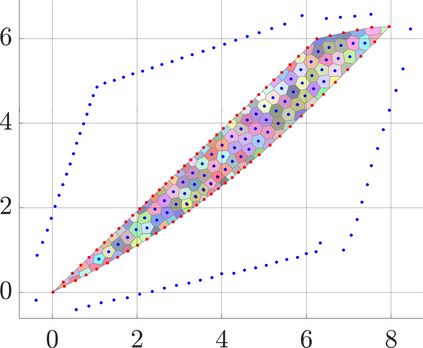
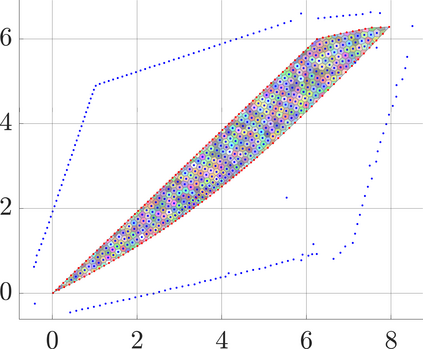
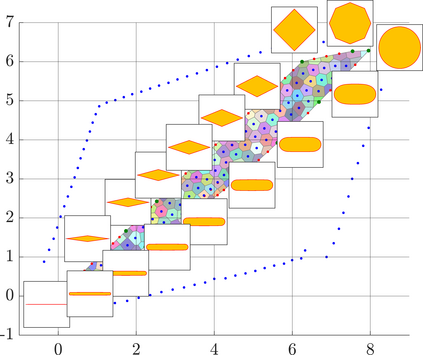
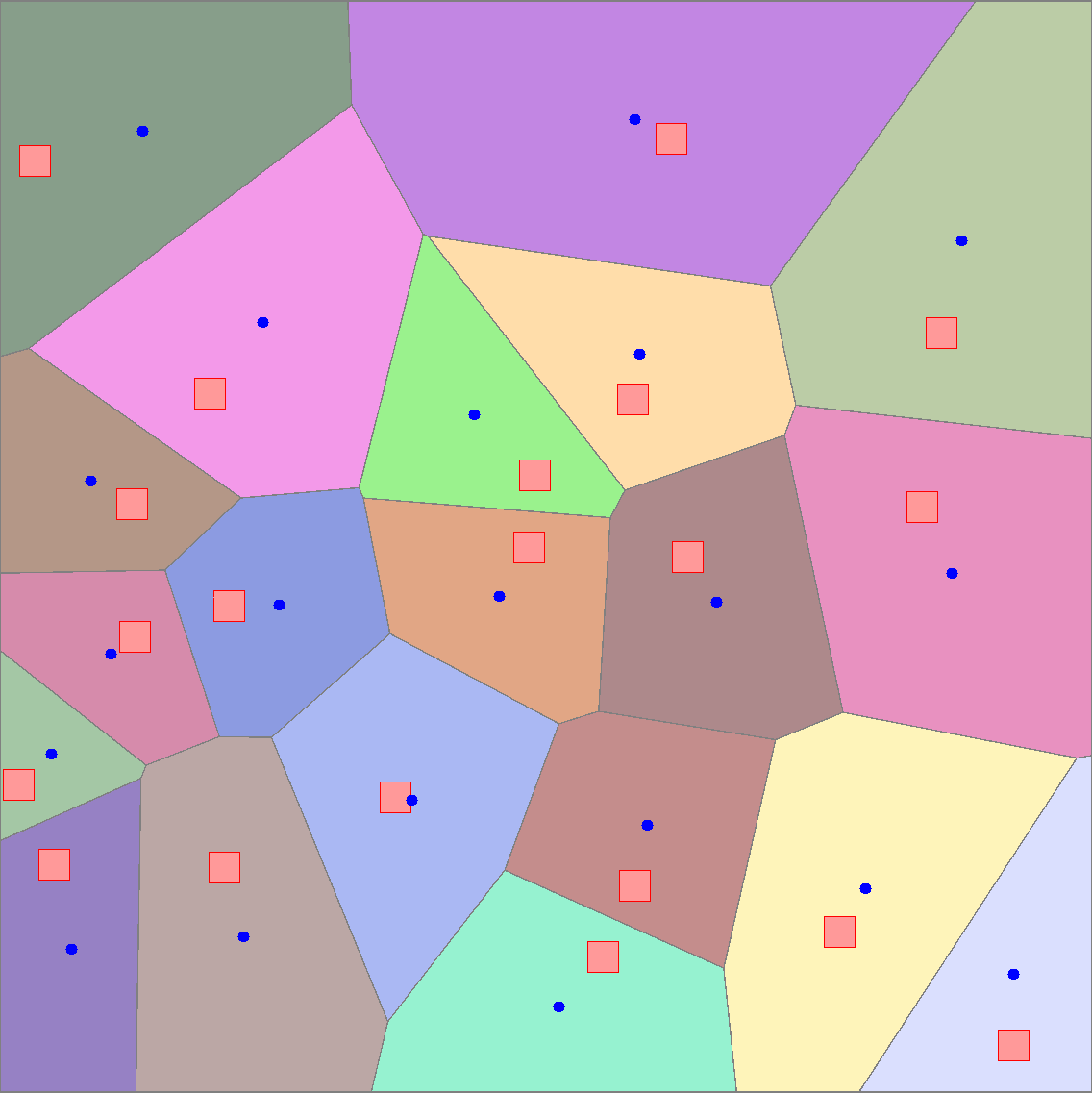
Identifying Blaschke-Santal\'o diagrams is an important topic that essentially consists in determining the image $Y=F(X)$ of a map $F:X\to{\mathbb{R}}^d$, where the dimension of the source space $X$ is much larger than the one of the target space. In some cases, that occur for instance in shape optimization problems, $X$ can even be a subset of an infinite-dimensional space. The usual Monte Carlo method, consisting in randomly choosing a number $N$ of points $x_1,\dots,x_N$ in $X$ and plotting them in the target space ${\mathbb{R}}^d$, produces in many cases areas in $Y$ of very high and very low concentration leading to a rather rough numerical identification of the image set. On the contrary, our goal is to choose the points $x_i$ in an appropriate way that produces a uniform distribution in the target space. In this way we may obtain a good representation of the image set $Y$ by a relatively small number $N$ of samples which is very useful when the dimension of the source space $X$ is large (or even infinite) and the evaluation of $F(x_i)$ is costly. Our method consists in a suitable use of {\it Centroidal Voronoi Tessellations} which provides efficient numerical results. Simulations for two and three dimensional examples are shown in the paper.