On a General Class of Orthogonal Learners for the Estimation of Heterogeneous Treatment Effects

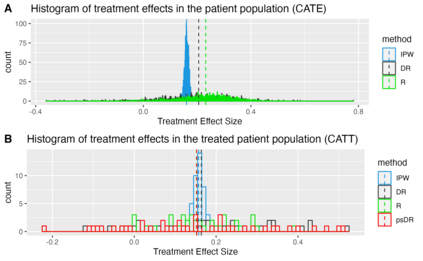
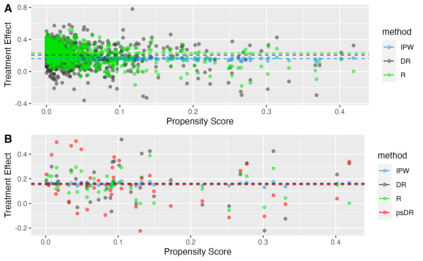
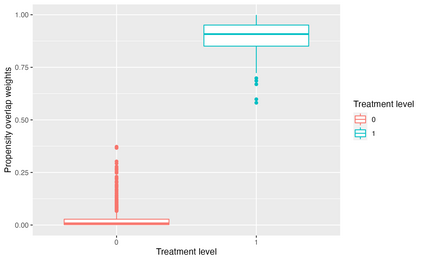
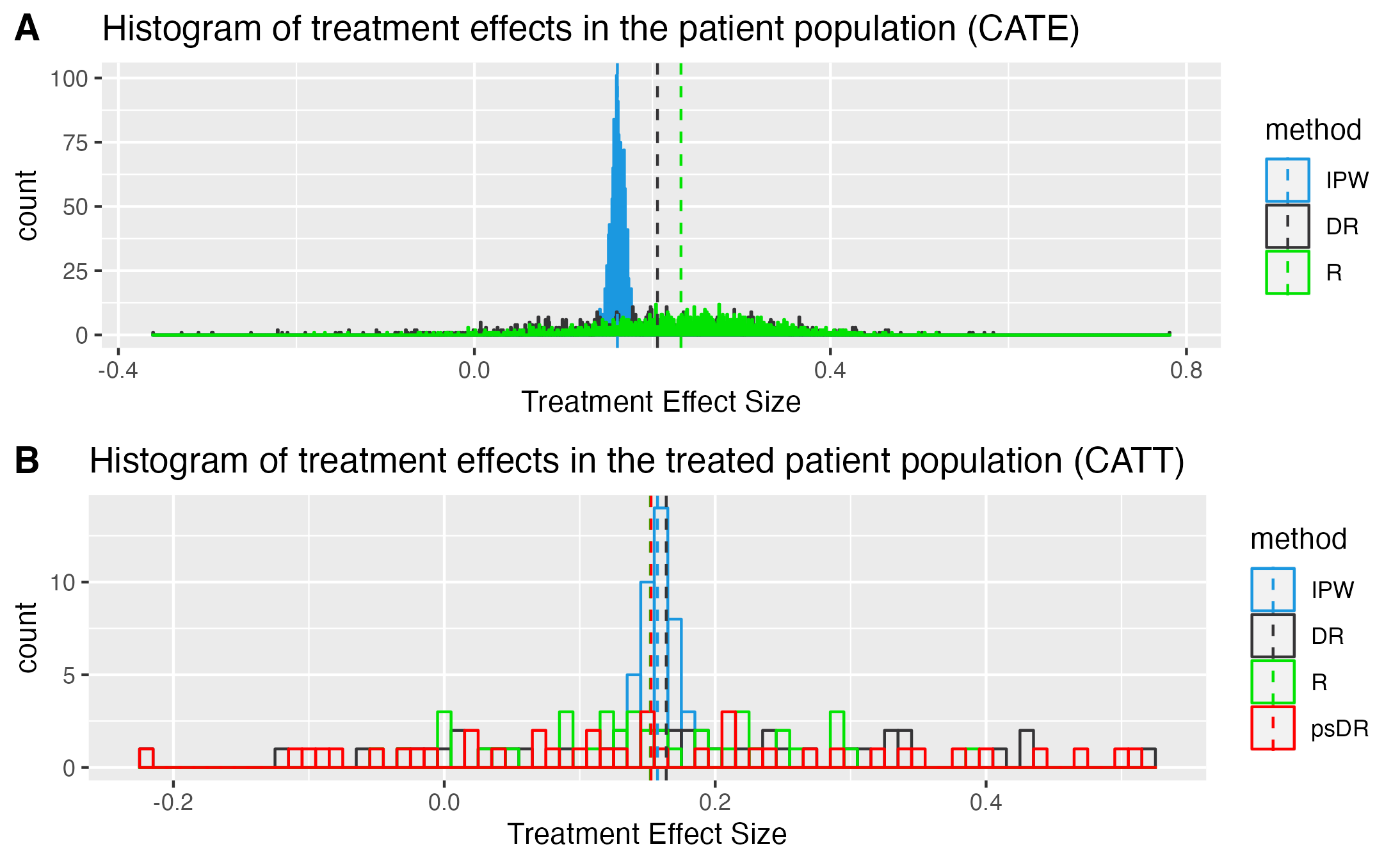
Motivated by applications in personalized medicine and individualized policy making, there is a growing interest in techniques for quantifying treatment effect heterogeneity in terms of the conditional average treatment effect (CATE). Some of the most prominent methods for CATE estimation developed in recent years are T-Learner, DR-Learner and R-Learner. The latter two were designed to improve on the former by being Neyman-orthogonal. However, the relations between them remain unclear, and likewise does the literature remain vague on whether these learners converge to a useful quantity or (functional) estimand when the underlying optimization procedure is restricted to a class of functions that does not include the CATE. In this article, we provide insight into these questions by discussing DR-learner and R-learner as special cases of a general class of Neyman-orthogonal learners for the CATE, for which we moreover derive oracle bounds. Our results shed light on how one may construct Neyman-orthogonal learners with desirable properties, on when DR-learner may be preferred over R-learner (and vice versa), and on novel learners that may sometimes be preferable to either of these. Theoretical findings are confirmed using results from simulation studies on synthetic data, as well as an application in critical care medicine.