Exact Gaussian Processes for Massive Datasets via Non-Stationary Sparsity-Discovering Kernels

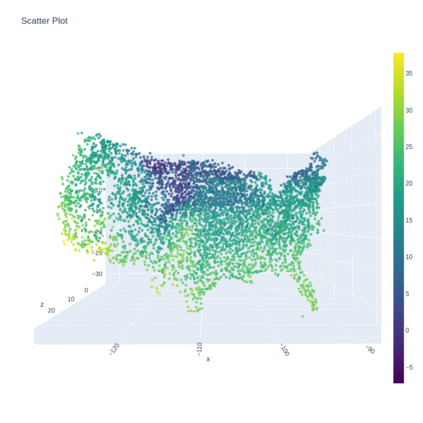
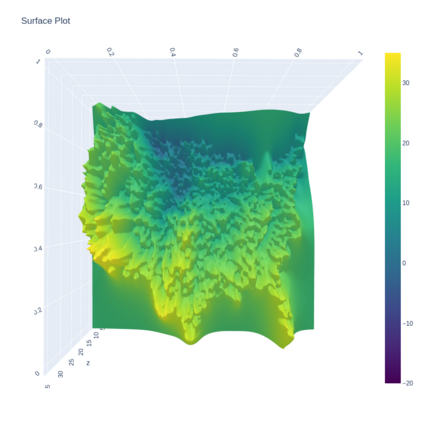
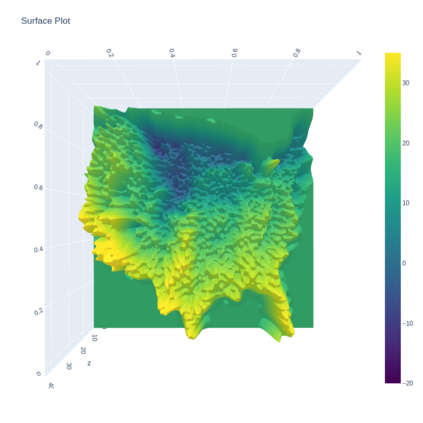
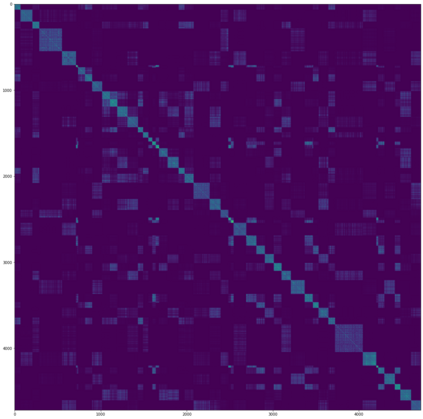
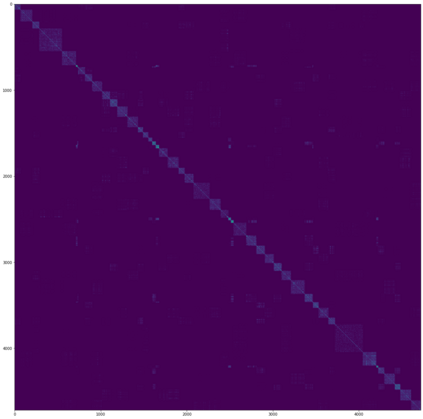
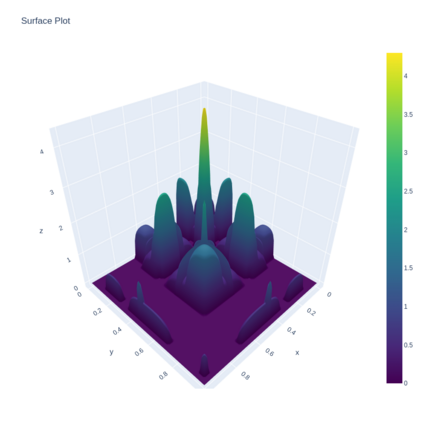
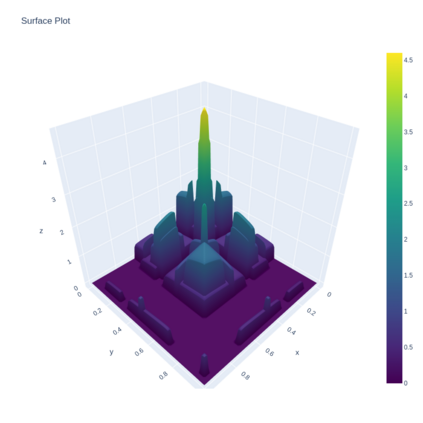
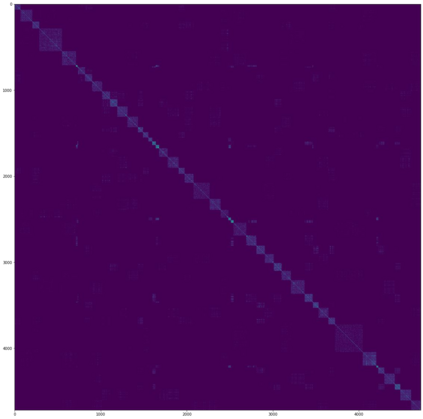
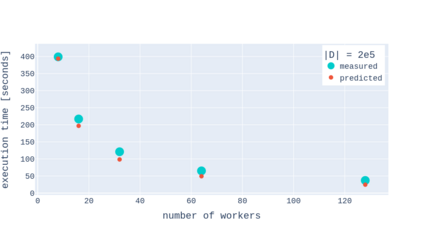
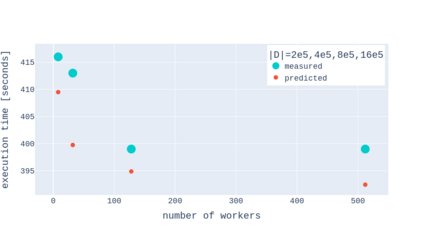
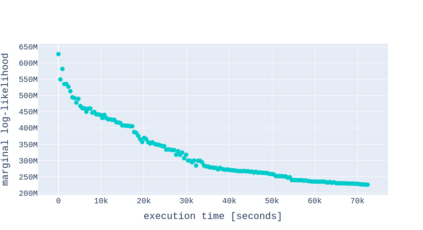
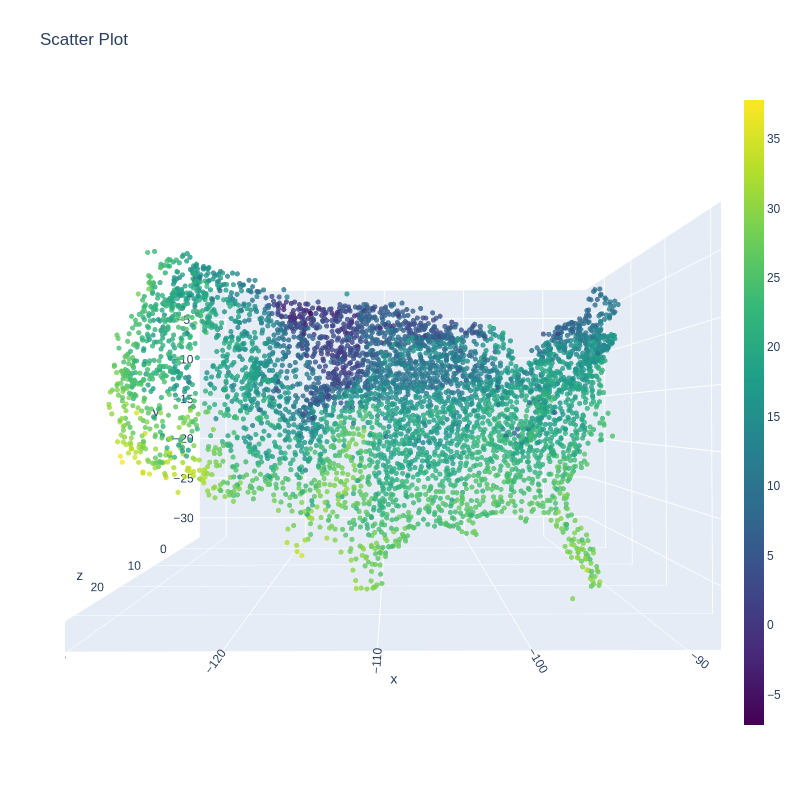
A Gaussian Process (GP) is a prominent mathematical framework for stochastic function approximation in science and engineering applications. This success is largely attributed to the GP's analytical tractability, robustness, non-parametric structure, and natural inclusion of uncertainty quantification. Unfortunately, the use of exact GPs is prohibitively expensive for large datasets due to their unfavorable numerical complexity of $O(N^3)$ in computation and $O(N^2)$ in storage. All existing methods addressing this issue utilize some form of approximation -- usually considering subsets of the full dataset or finding representative pseudo-points that render the covariance matrix well-structured and sparse. These approximate methods can lead to inaccuracies in function approximations and often limit the user's flexibility in designing expressive kernels. Instead of inducing sparsity via data-point geometry and structure, we propose to take advantage of naturally-occurring sparsity by allowing the kernel to discover -- instead of induce -- sparse structure. The premise of this paper is that GPs, in their most native form, are often naturally sparse, but commonly-used kernels do not allow us to exploit this sparsity. The core concept of exact, and at the same time sparse GPs relies on kernel definitions that provide enough flexibility to learn and encode not only non-zero but also zero covariances. This principle of ultra-flexible, compactly-supported, and non-stationary kernels, combined with HPC and constrained optimization, lets us scale exact GPs well beyond 5 million data points.