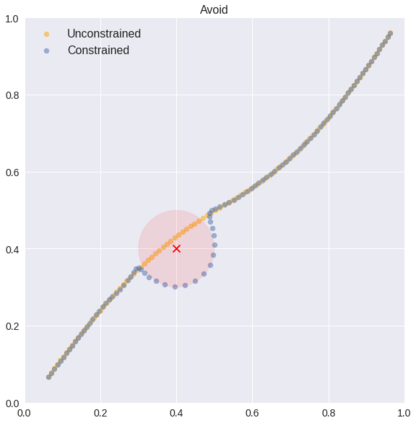
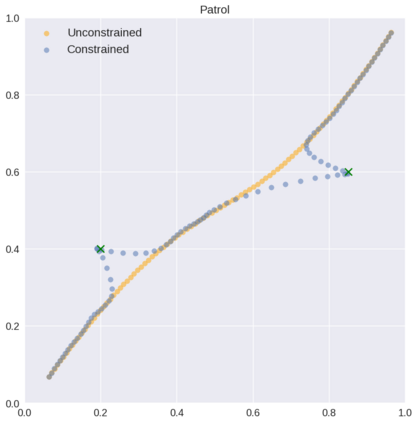
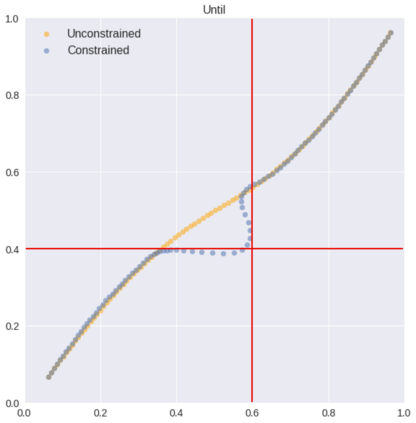
We introduce a theorem proving approach to the specification and generation of temporal logical constraints for training neural networks. We formalise a deep embedding of linear temporal logic over finite traces (LTL$_f$) and an associated evaluation function characterising its semantics within the higher-order logic of the Isabelle theorem prover. We then proceed to formalise a loss function $\mathcal{L}$ that we formally prove to be sound, and differentiable to a function $d\mathcal{L}$. We subsequently use Isabelle's automatic code generation mechanism to produce OCaml versions of LTL$_f$, $\mathcal{L}$ and $d\mathcal{L}$ that we integrate with PyTorch via OCaml bindings for Python. We show that, when used for training in an existing deep learning framework for dynamic movement, our approach produces expected results for common movement specification patterns such as obstacle avoidance and patrolling. The distinctive benefit of our approach is the fully rigorous method for constrained training, eliminating many of the risks inherent to ad-hoc implementations of logical aspects directly in an "unsafe" programming language such as Python.
翻译:我们为培训神经网络引入了一种理论验证方法,用于对神经网络进行培训的规格和生成时间逻辑约束。我们随后将线性时间逻辑的深度嵌入到有限的痕迹(LTL$-f$)上,并将一个相关的评价职能在伊莎贝尔理论证明的较高顺序逻辑范围内将其语义化。然后我们着手将一个损失函数($\mathcal{L}$)正规化,我们正式证明它健全,并且可以与一个函数($d\mathcal{L}$)不同。我们随后使用伊莎贝尔自动代码生成机制来生产OCaml版本的LTL$_f$、$\mathcal{L}和$d\mathcal{L}美元。我们通过OCaml对Python的捆绑物与PyTorrch融合起来。我们表明,当我们用于现有动态运动的深学习框架的培训时,我们的方法将产生预期的结果,比如避免和巡逻障碍等通用的动作规范模式。我们的方法的独特好处是完全严格地限制培训,消除了在逻辑方面“安全”的逻辑上应用中的许多风险。