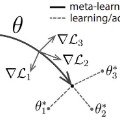
In this paper, we introduce a novel variation of model-agnostic meta-learning, where an extra multiplicative parameter is introduced in the inner-loop adaptation. Our variation creates a shortcut in the parameter space for the inner-loop adaptation and increases model expressivity in a highly controllable manner. We show both theoretically and numerically that our variation alleviates the problem of conflicting gradients and improves training dynamics. We conduct experiments on 3 distinctive problems, including a toy classification problem for threshold comparison, a regression problem for wavelet transform, and a classification problem on MNIST. We also discuss ways to generalize our method to a broader class of problems.
翻译:在本文中,我们引入了新颖的模型 -- -- 不可知元学习变异,在内环适应中引入了额外倍增参数。我们的变异在内环适应的参数空间中创造了捷径,并以高度可控的方式增加了模型的表达性。我们在理论上和数字上都显示,我们的变异缓解了冲突梯度问题,改善了培训动态。我们实验了三个不同的问题,包括用于临界点比较的玩具分类问题、波子变换的回归问题和MNIST的分类问题。我们还讨论了如何将我们的方法推广到更广泛的问题类别。