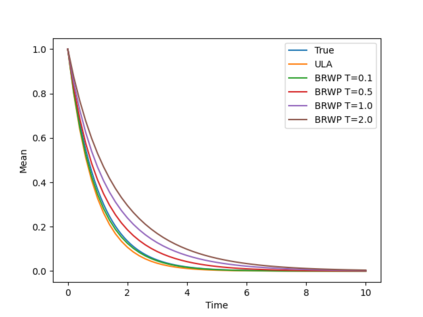
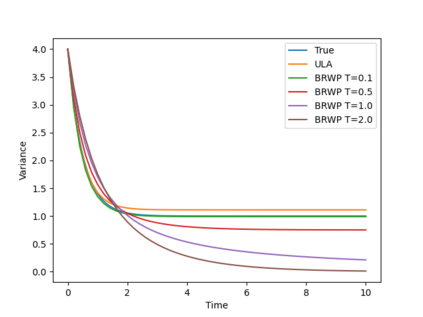
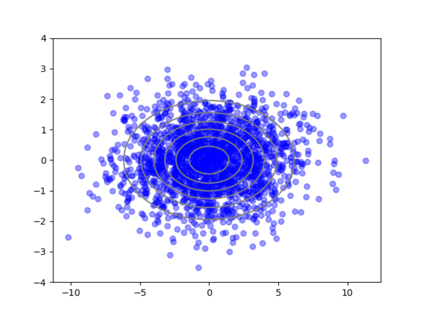
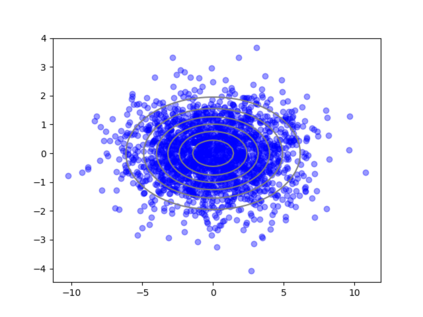
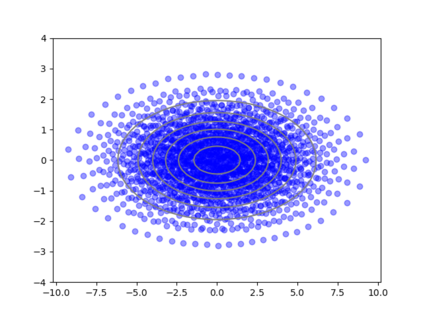
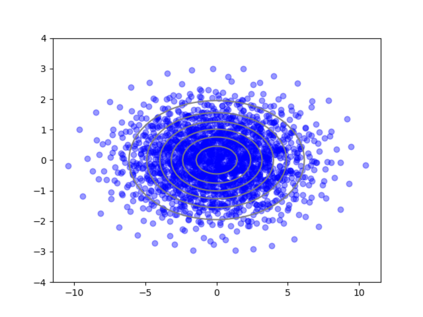
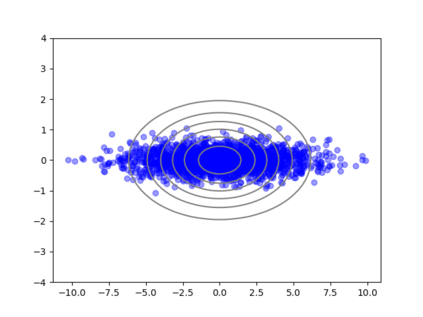
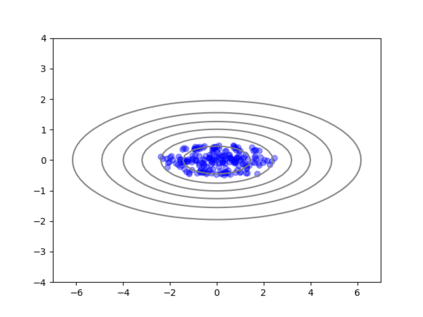
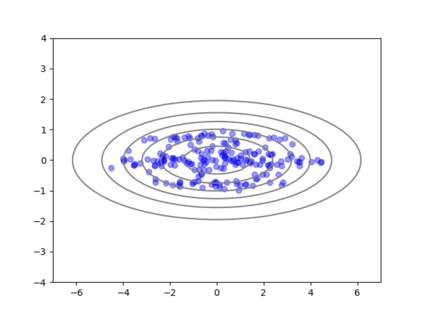
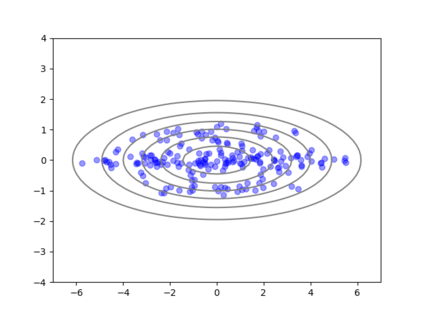
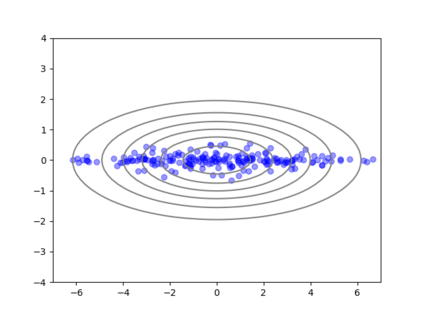
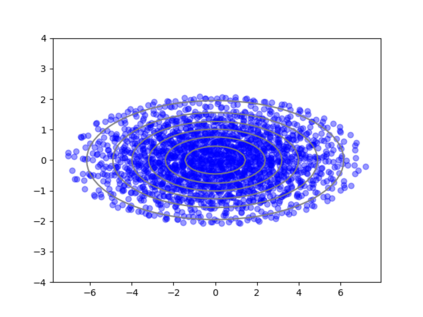
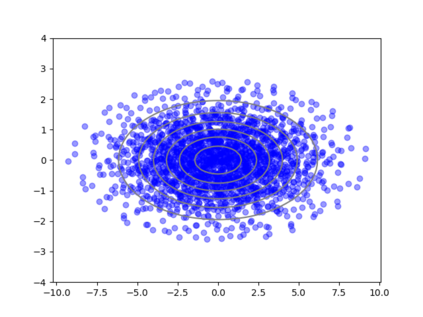
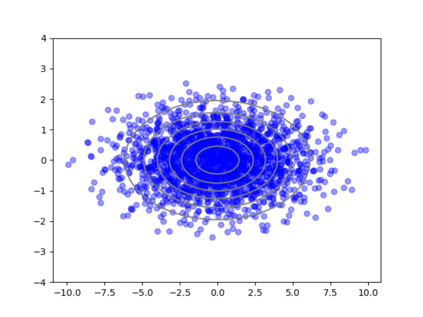
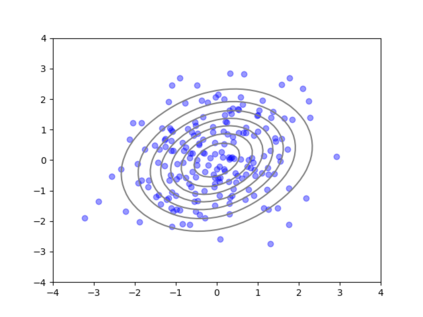
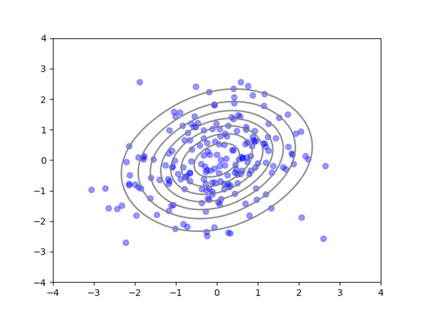
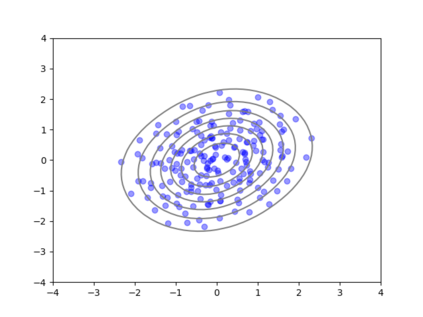
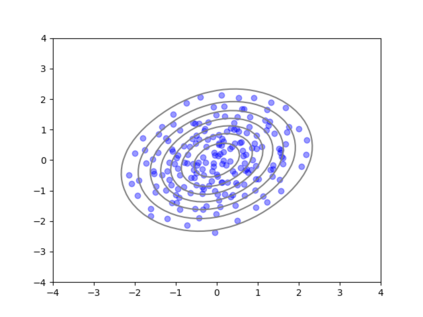
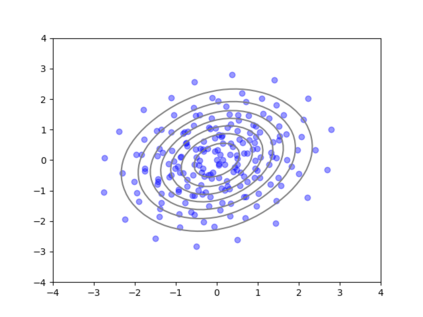
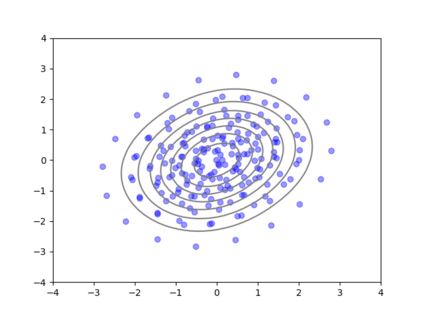
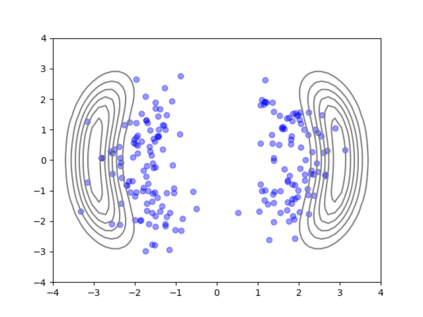
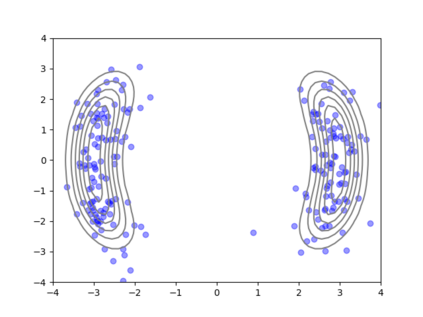
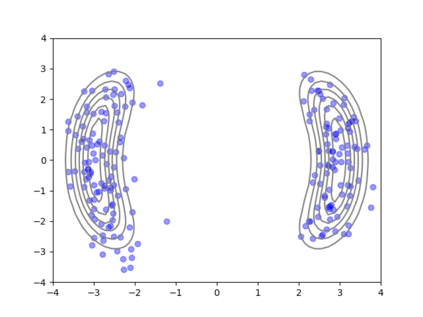
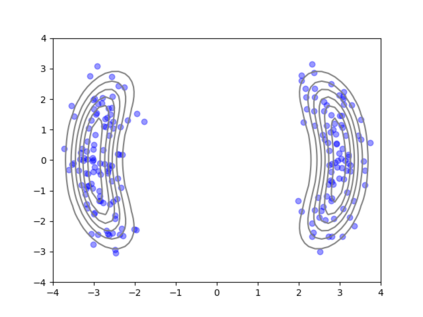
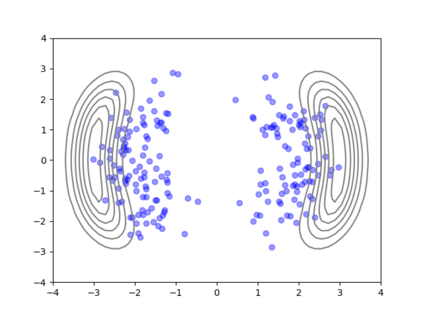
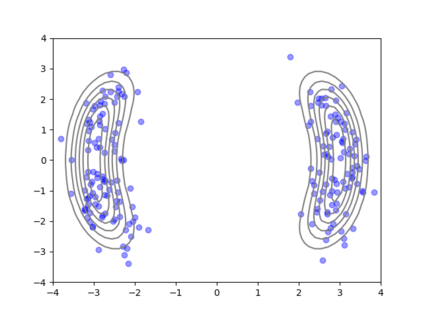
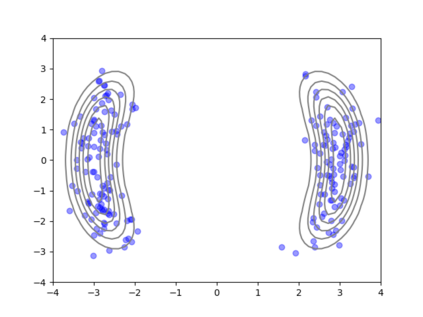
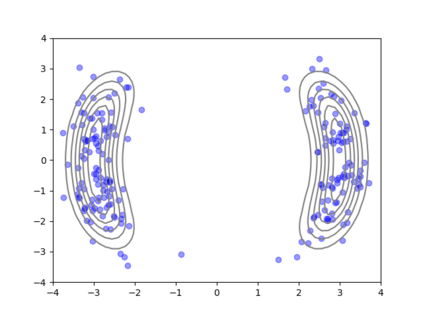
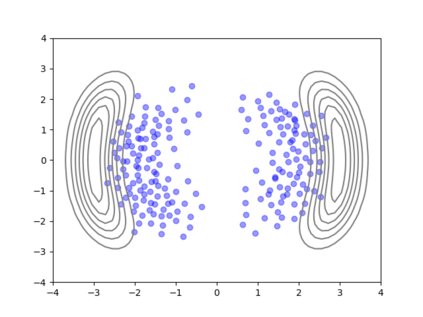
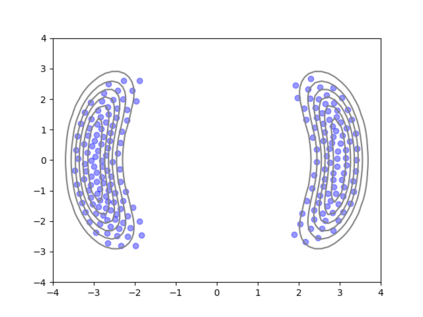
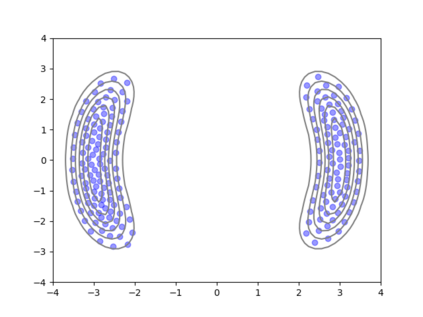
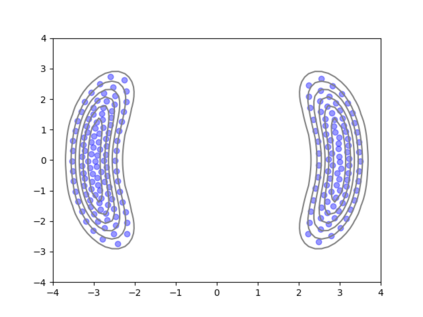
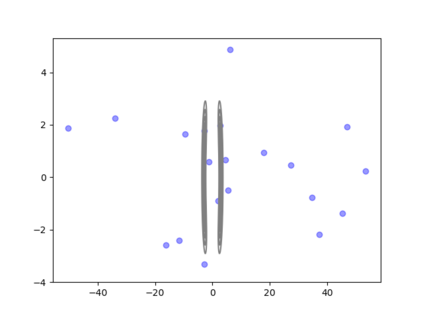
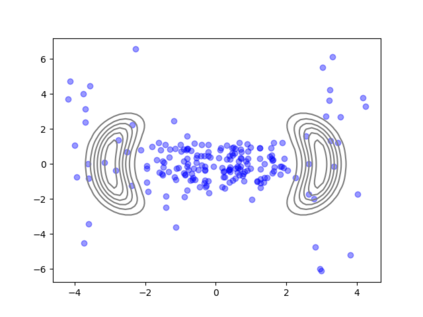
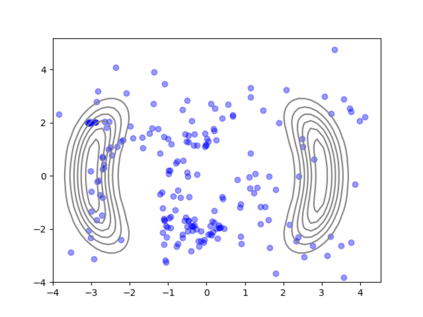
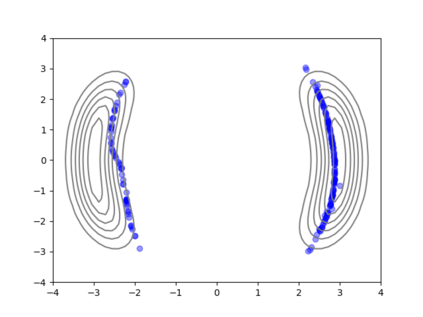
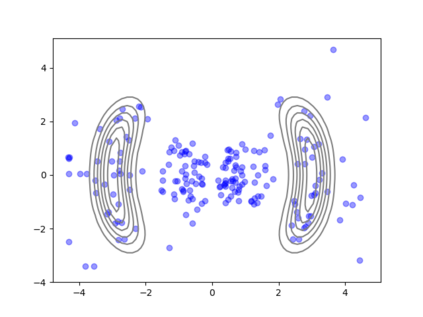
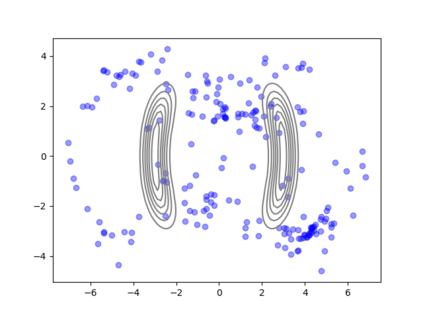
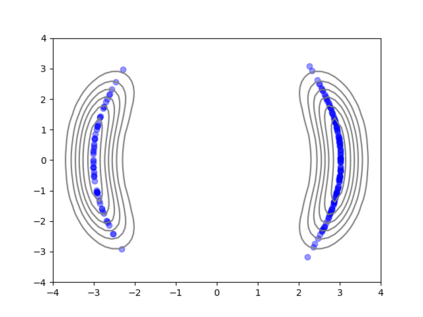
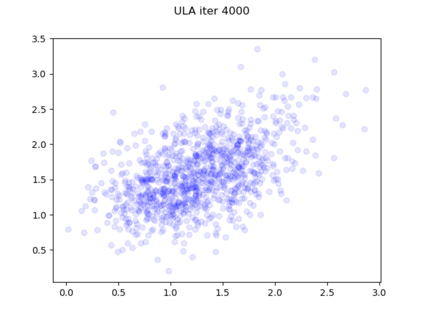
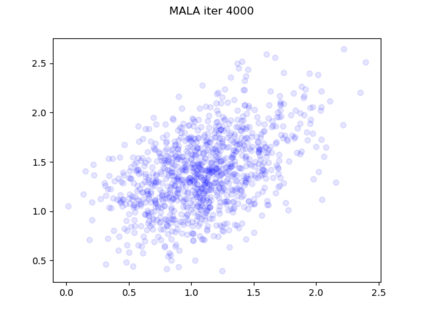
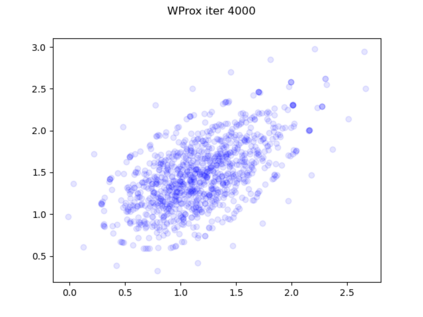
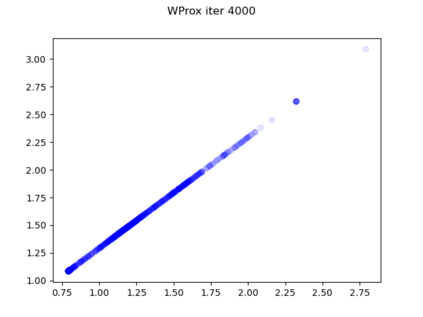
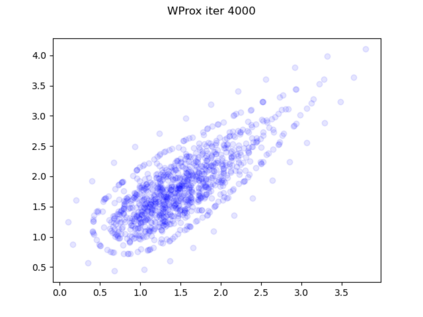
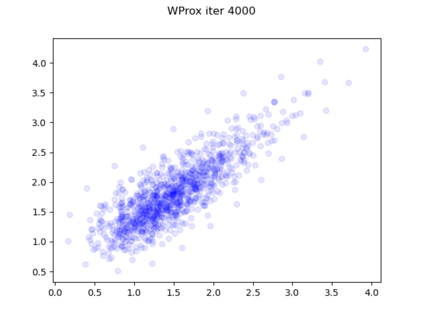
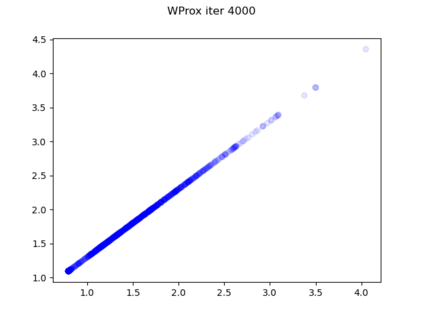
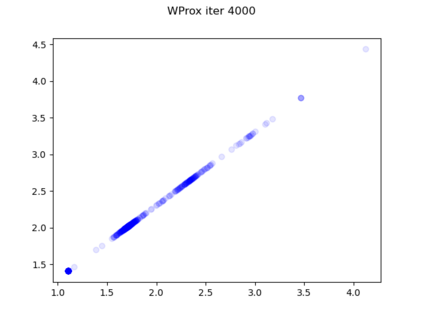
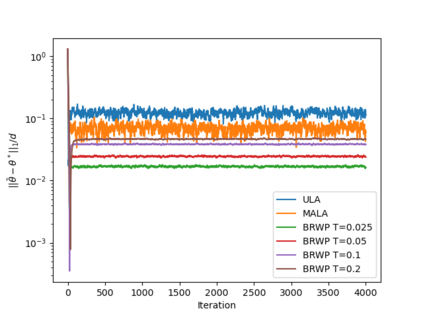
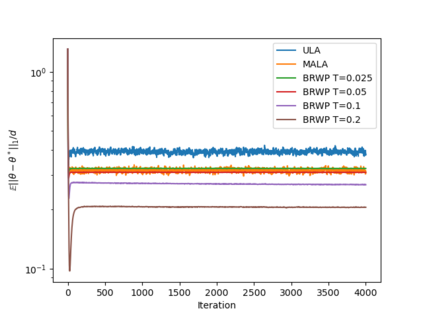
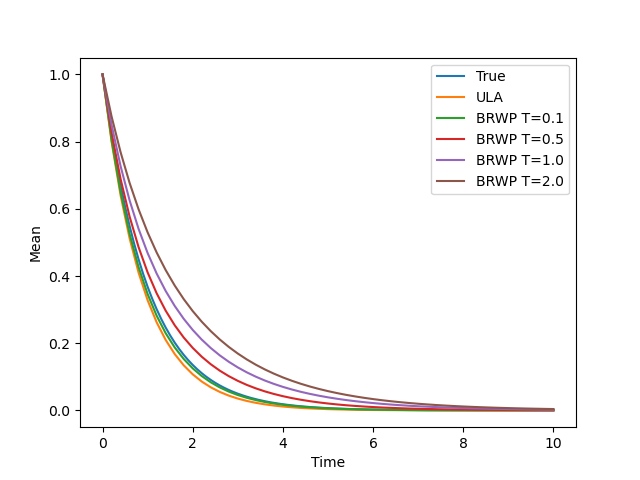
We consider the problem of sampling from a distribution governed by a potential function. This work proposes an explicit score based MCMC method that is deterministic, resulting in a deterministic evolution for particles rather than a stochastic differential equation evolution. The score term is given in closed form by a regularized Wasserstein proximal, using a kernel convolution that is approximated by sampling. We demonstrate fast convergence on various problems and show improved dimensional dependence of mixing time bounds for the case of Gaussian distributions compared to the unadjusted Langevin algorithm (ULA) and the Metropolis-adjusted Langevin algorithm (MALA). We additionally derive closed form expressions for the distributions at each iterate for quadratic potential functions, characterizing the variance reduction. Empirical results demonstrate that the particles behave in an organized manner, lying on level set contours of the potential. Moreover, the posterior mean estimator of the proposed method is shown to be closer to the maximum a-posteriori estimator compared to ULA and MALA in the context of Bayesian logistic regression. Additional examples demonstrate competitive performance for Bayesian neural network training.
翻译:暂无翻译