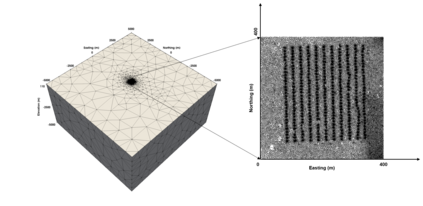
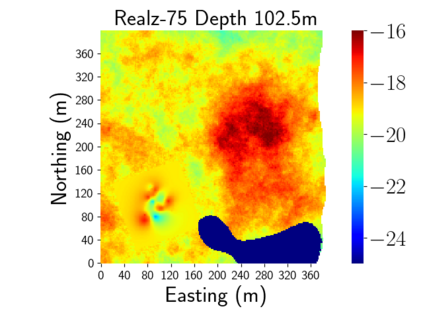
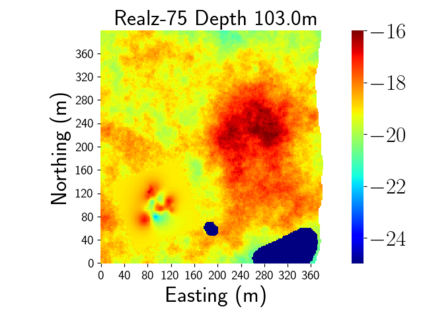
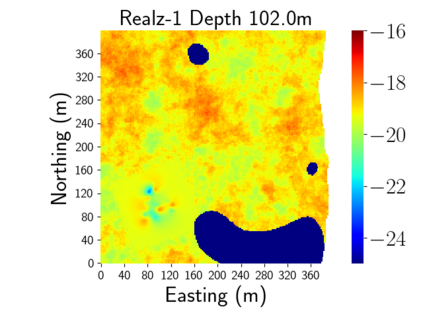
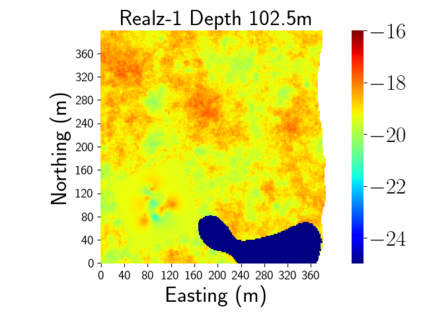
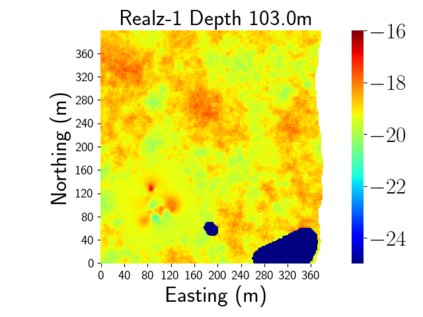
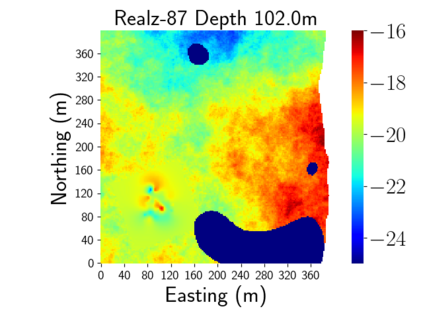
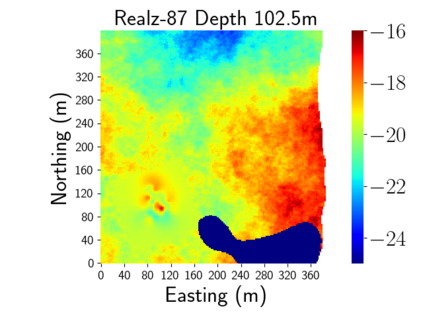
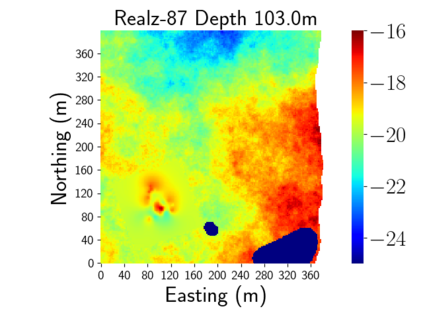
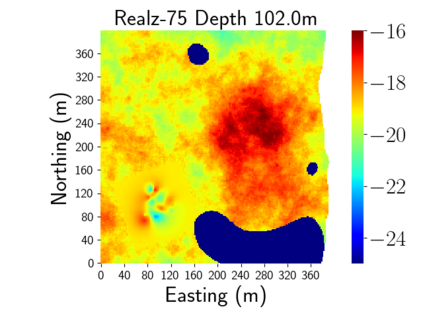
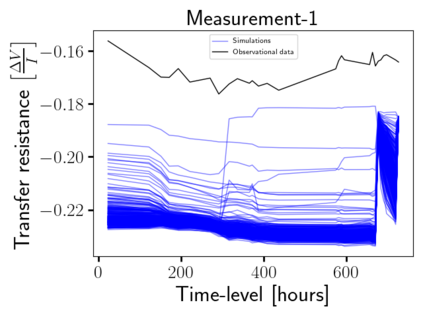
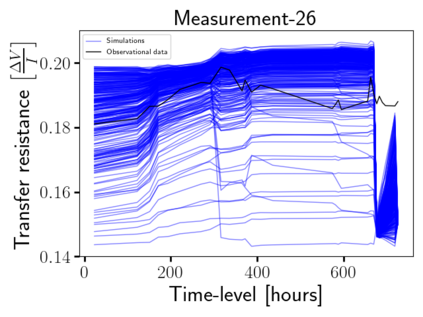
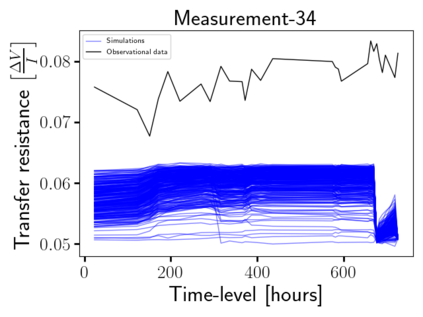
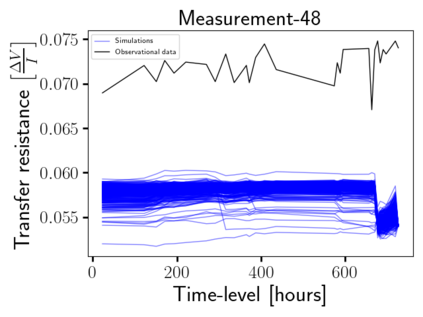
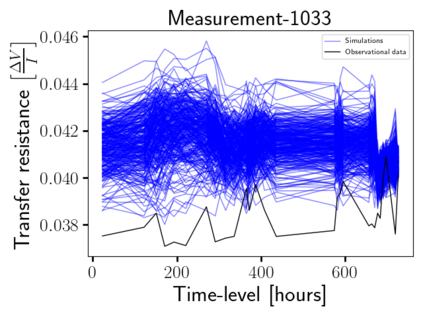
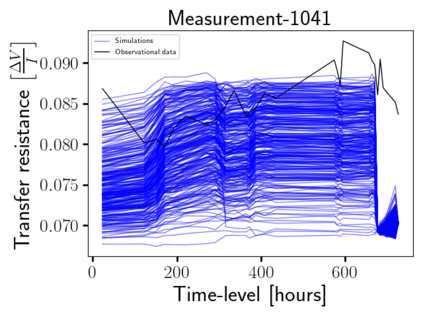
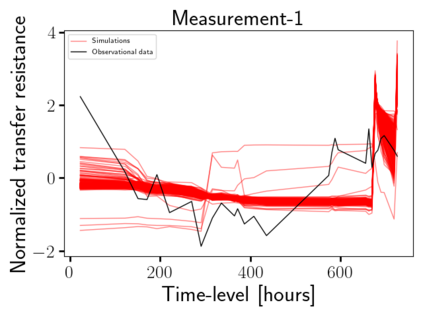
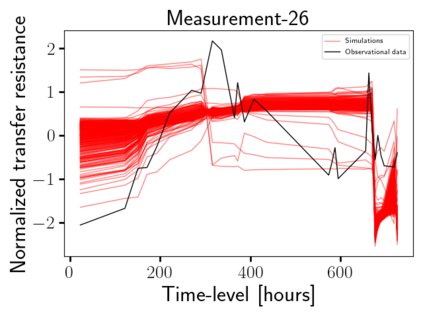
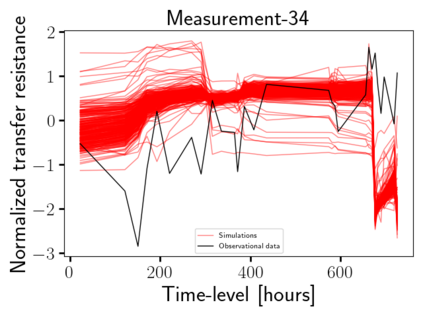
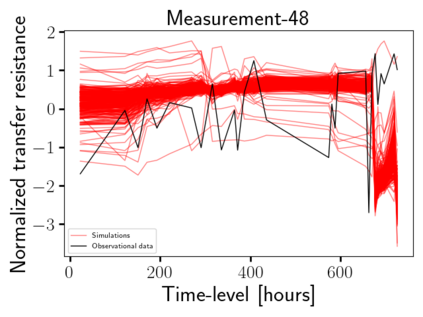
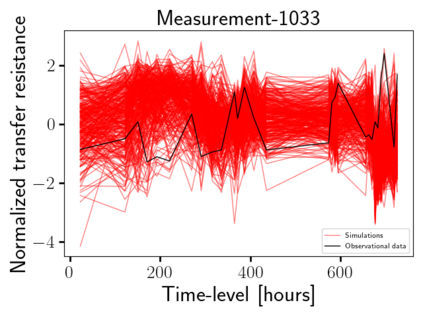
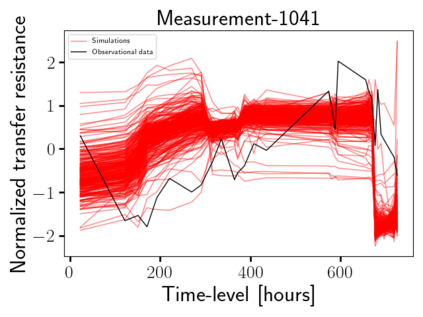
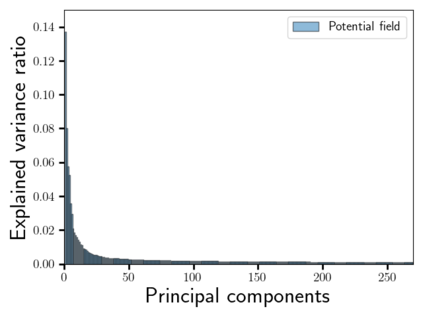
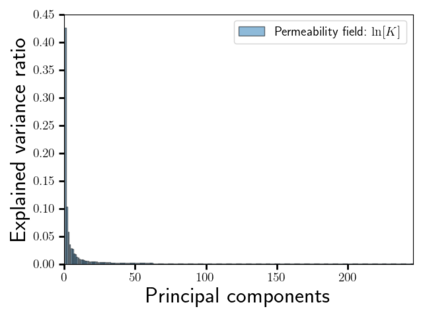
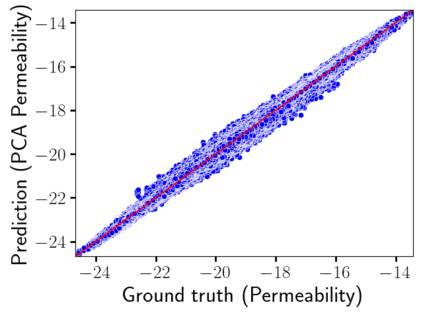
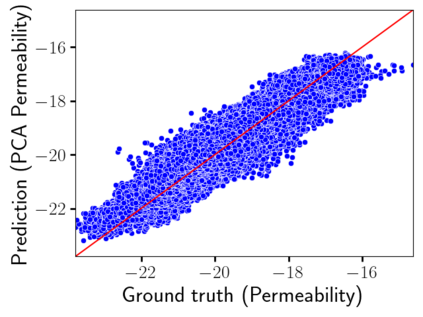
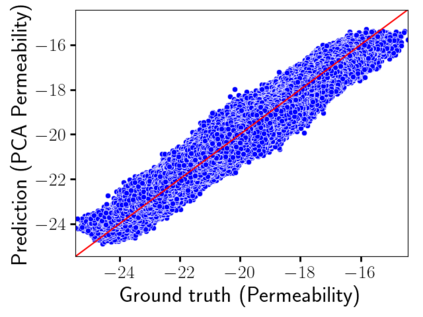
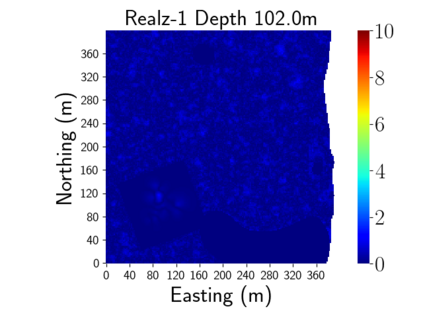
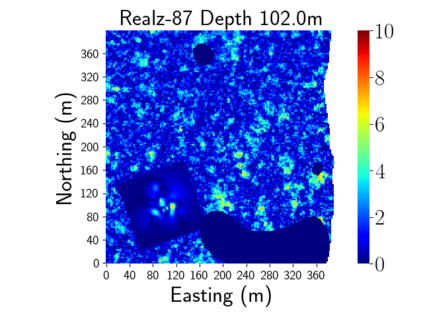
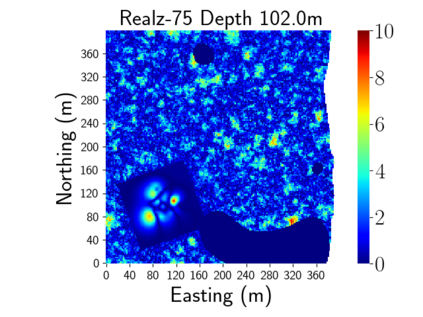
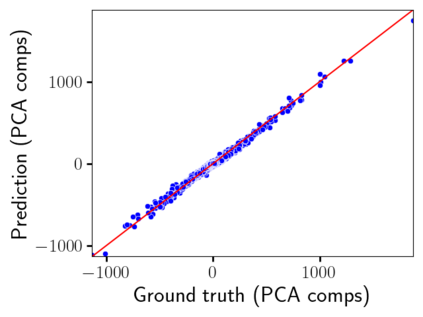
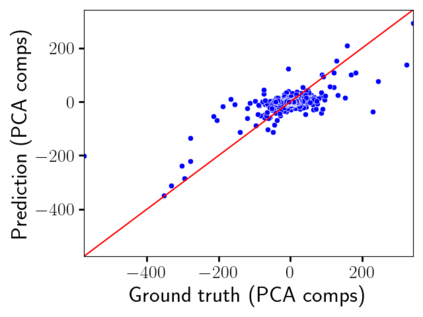
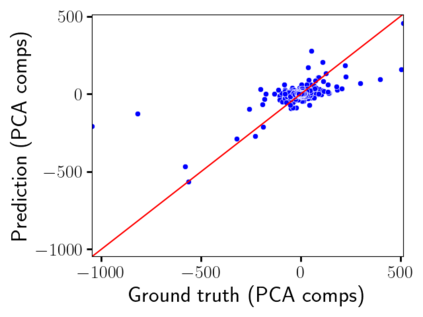
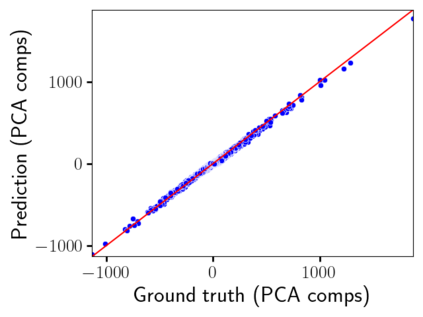
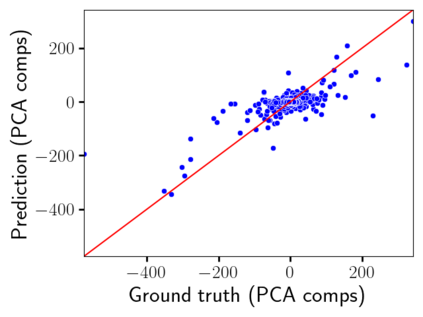
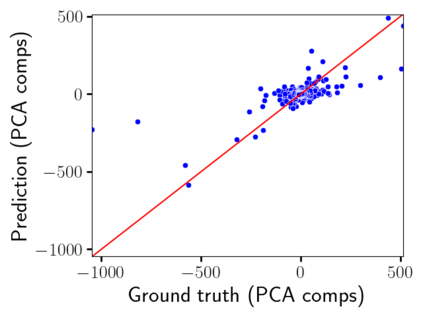
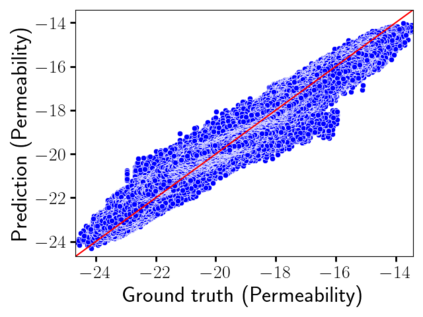
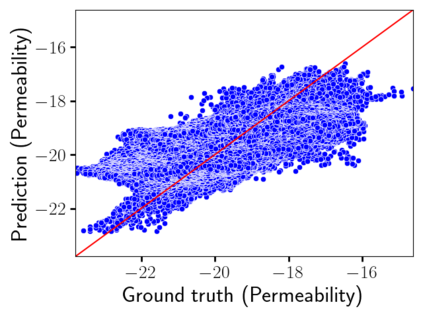
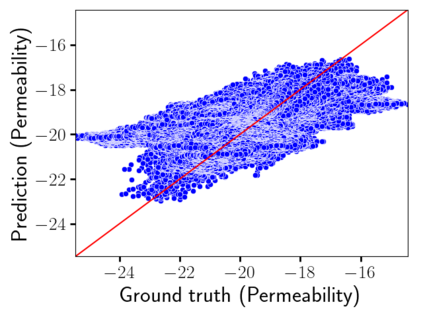
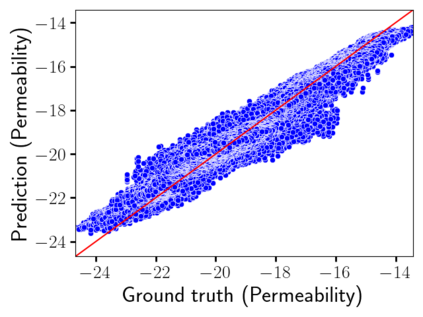
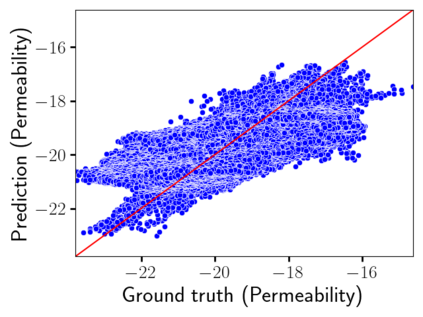
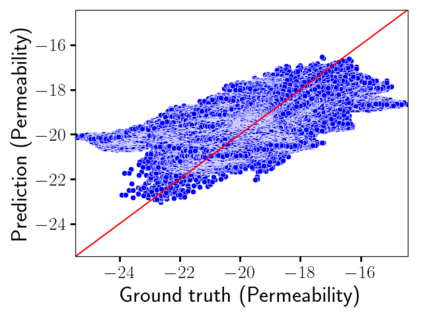
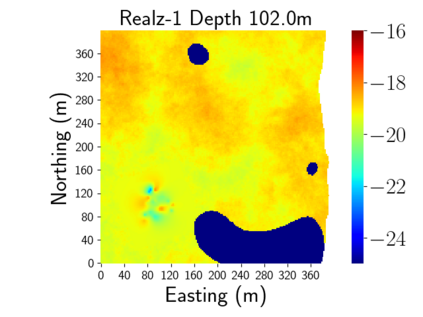
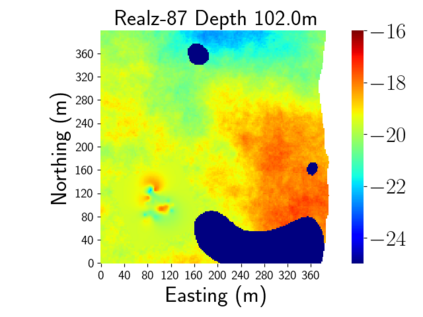
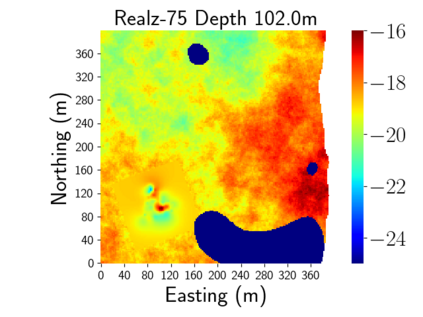
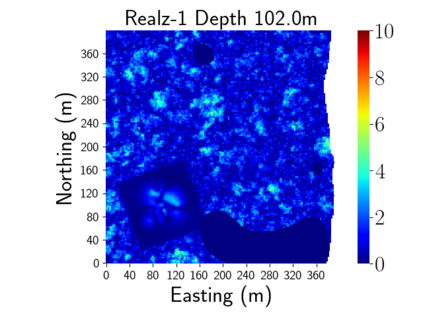
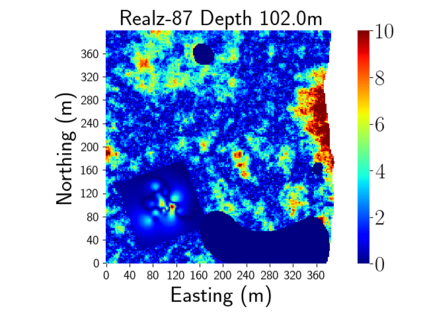
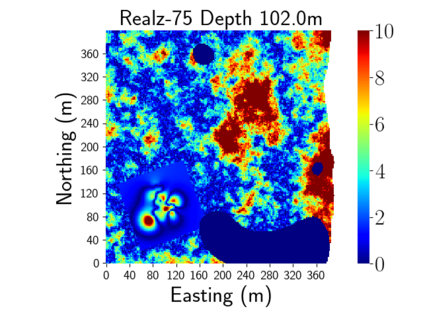
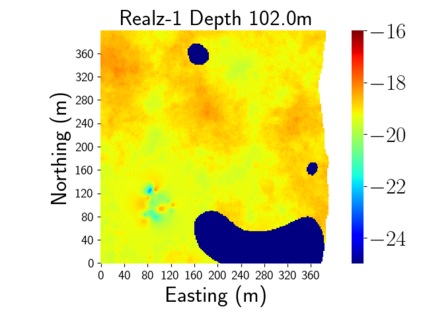
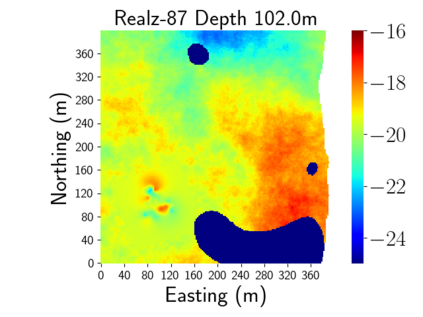
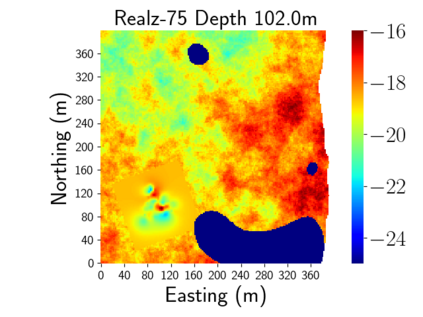
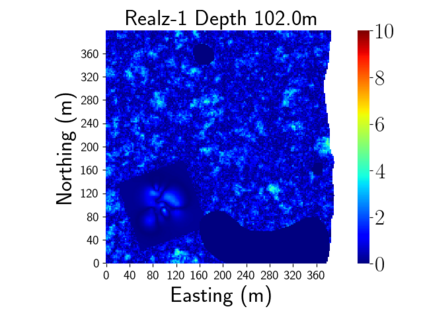
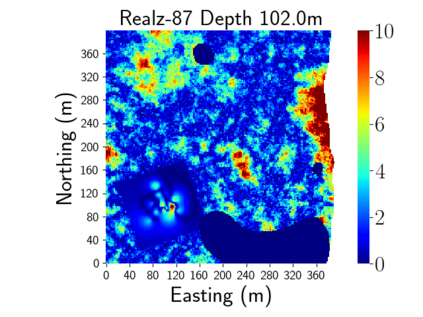
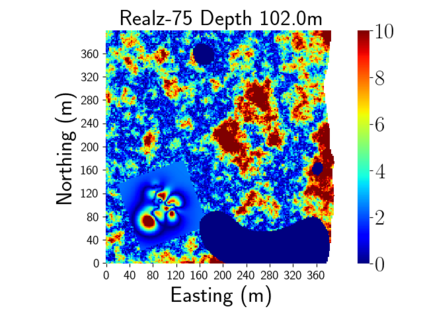
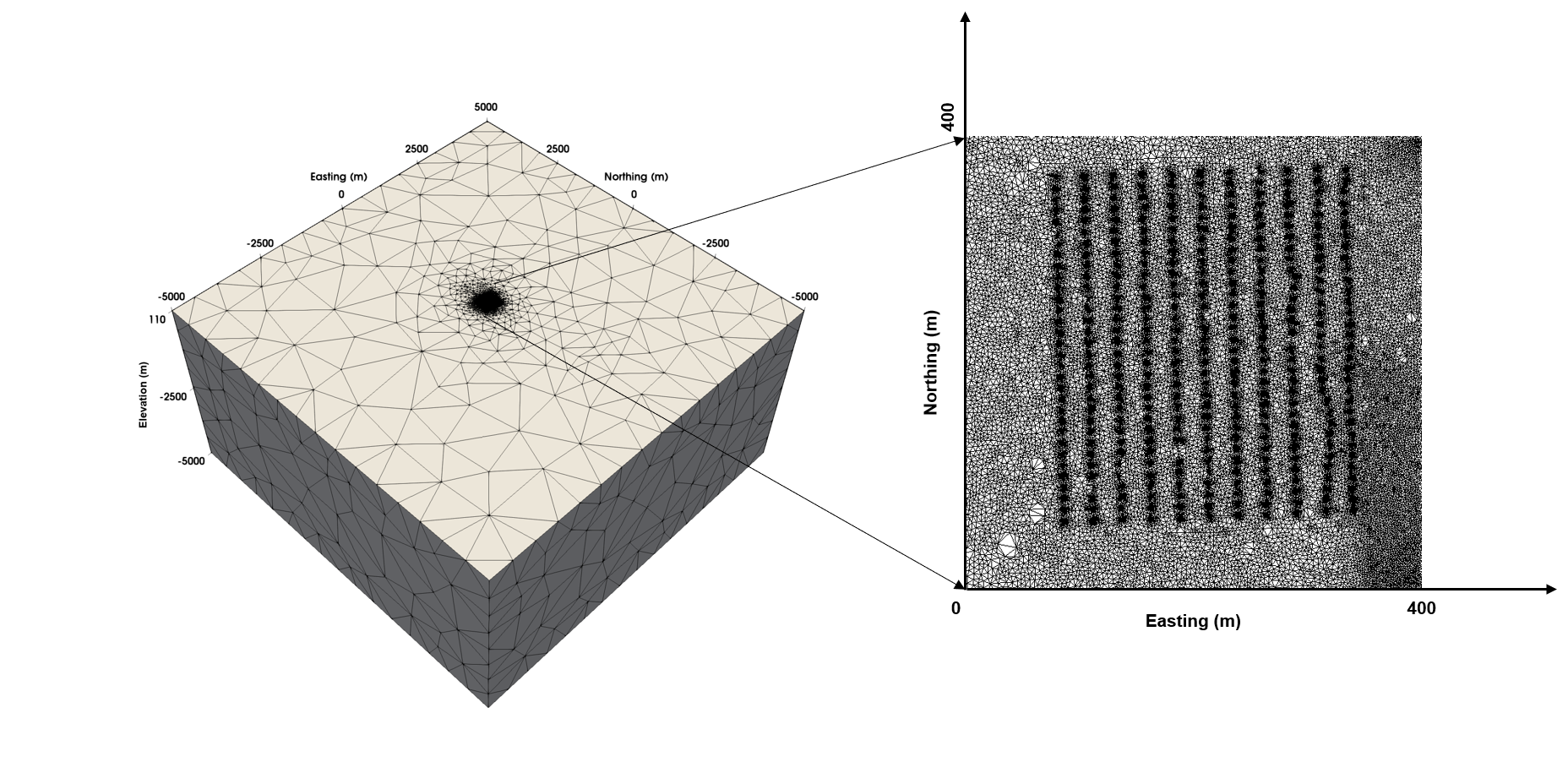
Time-lapse electrical resistivity tomography (ERT) is a popular geophysical method to estimate three-dimensional (3D) permeability fields from electrical potential difference measurements. Traditional inversion and data assimilation methods are used to ingest this ERT data into hydrogeophysical models to estimate permeability. Due to ill-posedness and the curse of dimensionality, existing inversion strategies provide poor estimates and low resolution of the 3D permeability field. Recent advances in deep learning provide us with powerful algorithms to overcome this challenge. This paper presents a deep learning (DL) framework to estimate the 3D subsurface permeability from time-lapse ERT data. To test the feasibility of the proposed framework, we train DL-enabled inverse models on simulation data. Subsurface process models based on hydrogeophysics are used to generate this synthetic data for deep learning analyses. Results show that proposed weak supervised learning can capture salient spatial features in the 3D permeability field. Quantitatively, the average mean squared error (in terms of the natural log) on the strongly labeled training, validation, and test datasets is less than 0.5. The R2-score (global metric) is greater than 0.75, and the percent error in each cell (local metric) is less than 10%. Finally, an added benefit in terms of computational cost is that the proposed DL-based inverse model is at least O(104) times faster than running a forward model. Note that traditional inversion may require multiple forward model simulations (e.g., in the order of 10 to 1000), which are very expensive. This computational savings (O(105) - O(107)) makes the proposed DL-based inverse model attractive for subsurface imaging and real-time ERT monitoring applications due to fast and yet reasonably accurate estimations of the permeability field.
翻译:(ERT) 一个流行的地球物理方法, 用来估计三维( 3D) 透视场, 从电子潜在差异的测量中估算出三维( 3D) 渗透场。 使用传统的翻版和数据同化方法, 将这一ERT数据浸入水文地球物理模型, 以估计渗透性。 由于水深和维度的诅咒, 现有的反转战略为 3D 渗透性字段提供了低估计和低分辨率。 最近深层次学习的进展为我们提供了强大的算法, 以克服这一挑战。 本文展示了一个深度学习( DL ) 框架, 以估算从电流时落ERER 数据中估算 3D( 3D 3D) 深层( D) 渗透性( DD) 渗透性( DL ) 渗透性( DL ) 渗透性( DL ) 的渗透性( DV) 透性( DL ) 透性(D) 透性(DO- 平面值值 ) 和 數值( 數值( 數值( 值) 數值( 值) 值( 值) 數值( 值) 值( 值( 值) 值) 值( 值) 值( 值) 值( 值) 值( 值) 值) 值( 值) 值) 值( 值) 值) 值( 值) 值) 值) 值( 值( 值) 值) 值(比 值) 值) 值( 值) 值( 值( 值) 值( 值) 值) 值( 值( 值) 值) 值) ) 值) 值) 值( ) 值) 值( ) ) 值) 值) 值 (比 值( 值 值 值( 值 值 值 值 值 值) 值 值 ) 值 值) 值) 值) 值) 值) 值) 值) 值) 值( 值( 值) 值( 值( 值) 值)