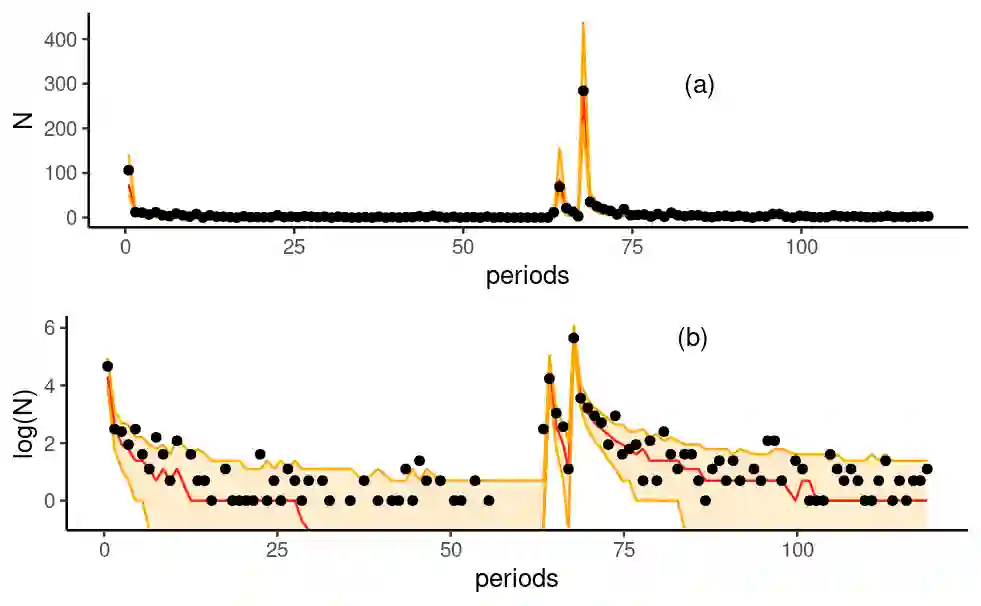
Hawkes process are very popular mathematical tools for modelling phenomena exhibiting a \textit{self-exciting} or \textit{self-correcting} behaviour. Typical examples are earthquakes occurrence, wild-fires, drought, capture-recapture, crime violence, trade exchange, and social network activity. The widespread use of Hawkes process in different fields calls for fast, reproducible, reliable, easy-to-code techniques to implement such models. We offer a technique to perform approximate Bayesian inference of Hawkes process parameters based on the use of the R-package \inlabru. The \inlabru R-package, in turn, relies on the INLA methodology to approximate the posterior of the parameters. Our Hawkes process approximation is based on a decomposition of the log-likelihood in three parts, which are linearly approximated separately. The linear approximation is performed with respect to the mode of the parameters' posterior distribution, which is determined with an iterative gradient-based method. The approximation of the posterior parameters is therefore deterministic, ensuring full reproducibility of the results. The proposed technique only requires the user to provide the functions to calculate the different parts of the decomposed likelihood, which are internally linearly approximated by the R-package \inlabru. We provide a comparison with the \bayesianETAS R-package which is based on an MCMC method. The two techniques provide similar results but our approach requires two to ten times less computational time to converge, depending on the amount of data.
翻译:霍克斯进程是非常流行的数学工具,用于模拟显示行为行为\ textit{ 自我激发} 或\ textit{ 自我修正} 的现象。 典型的例子有地震发生、 野火、 干旱、 抓回- 抓回、 犯罪暴力、 交易交换 和社会网络活动。 霍克斯进程在不同领域广泛使用, 需要快速、 可复制、 可靠、 容易到编码的技术来执行这些模型。 我们提供一种技术, 以使用 R- package \ inlabru 或\ textit{ self- 纠正} 来对霍克斯进程进程参数进行大约的推断。 辛拉布鲁 R- 包包 反过来, 依靠 INLA 方法来接近参数的表面。 我们霍克斯进程靠三个部分的对日志相似性进行分解, 这三部分是线性比较。 线性近于参数的分布模式, 由迭代梯基方法决定。 近的参数参数参数参数参数参数参数参数的精确比对我们的计算结果进行两次比较, 因此, 需要完全的精确的计算方法的精确值 。 只能提供正确的计算结果 。 。 向内部的精确计算结果 。