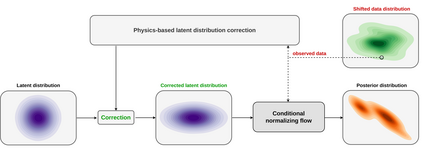
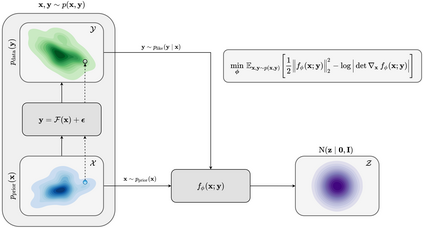
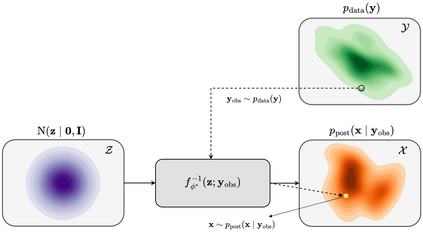
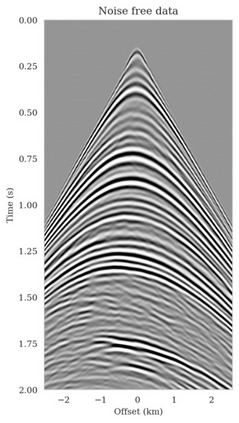
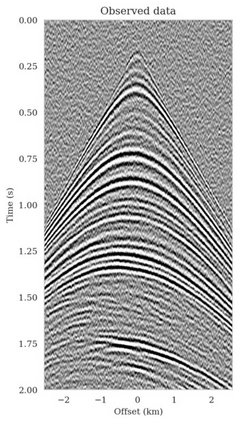
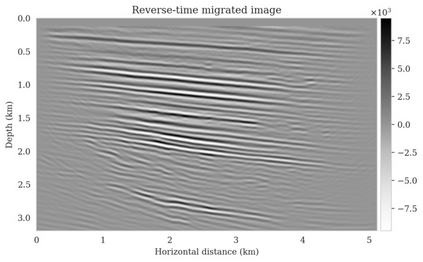
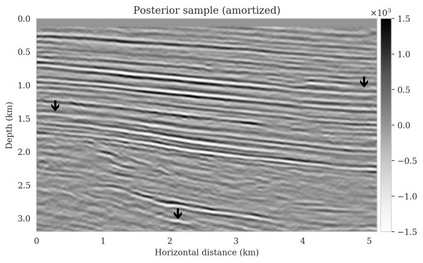
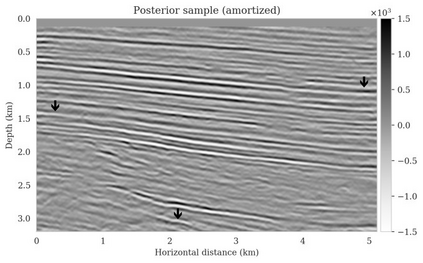
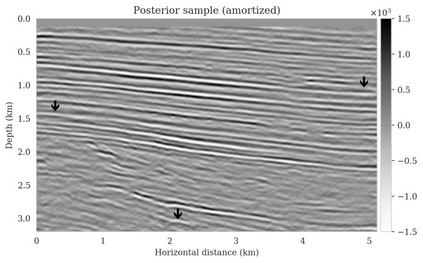
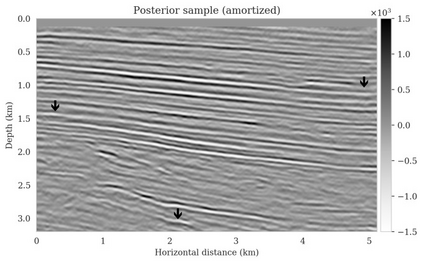
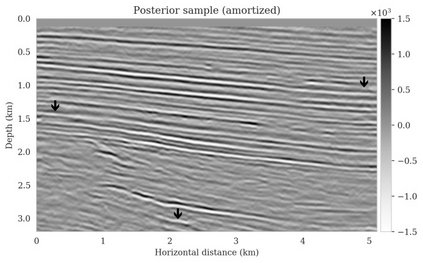
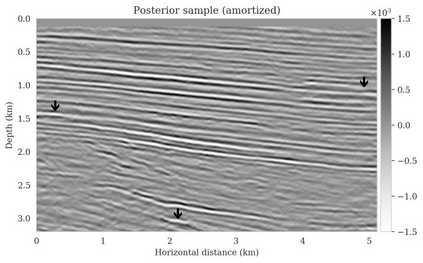
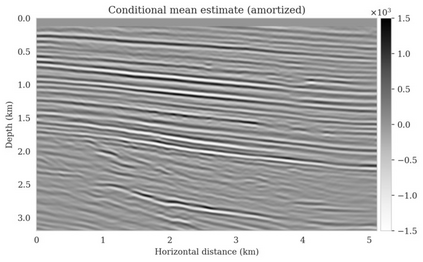
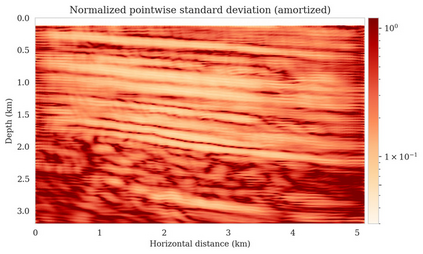
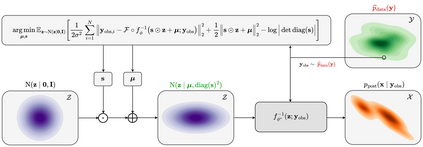
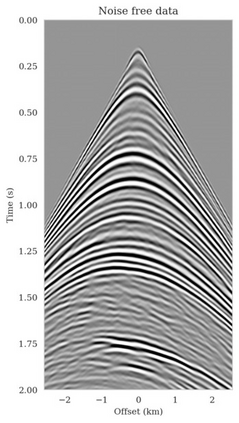
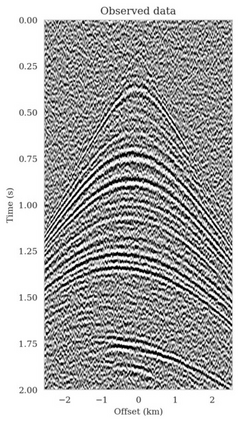
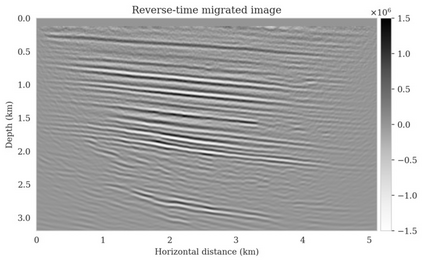
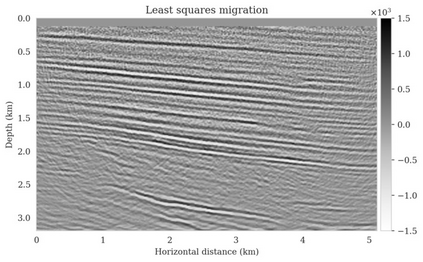
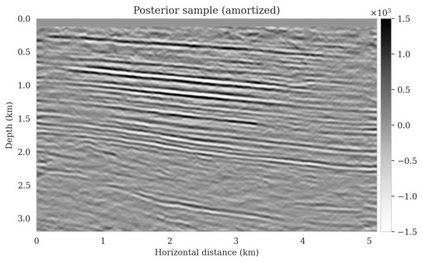
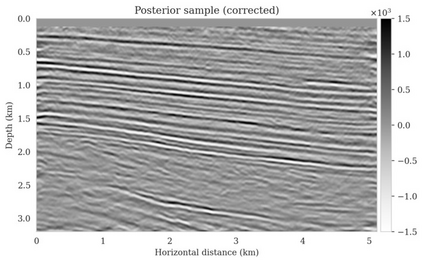
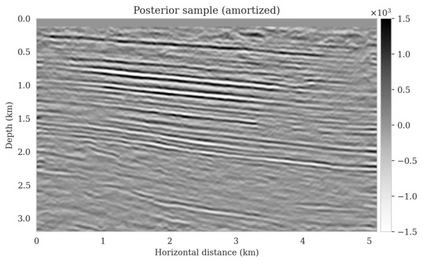
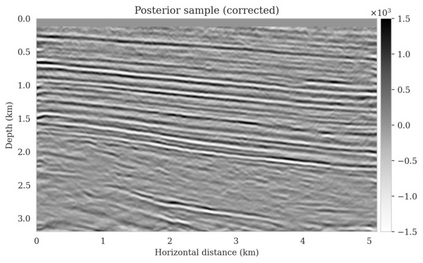
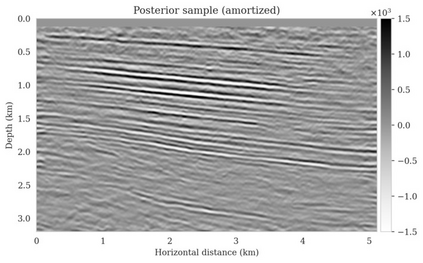
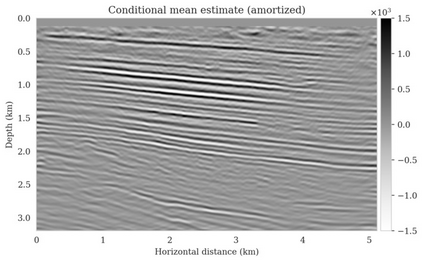
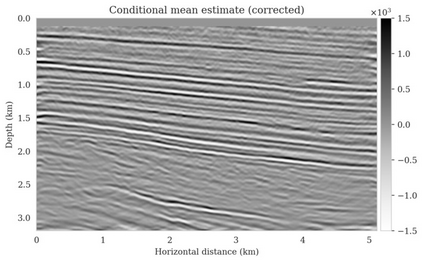
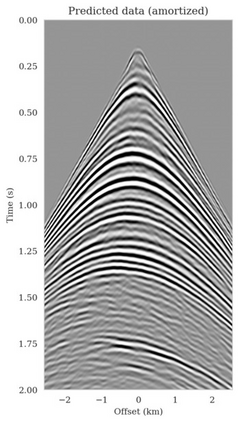
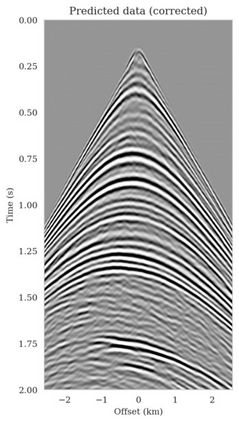
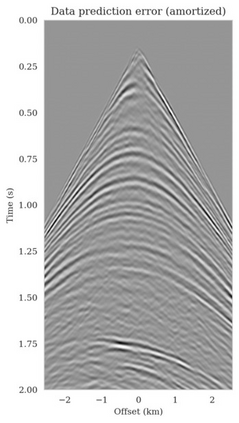
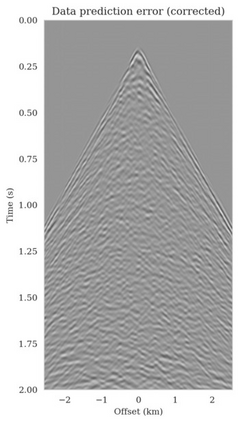
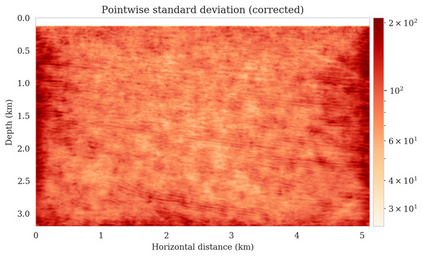
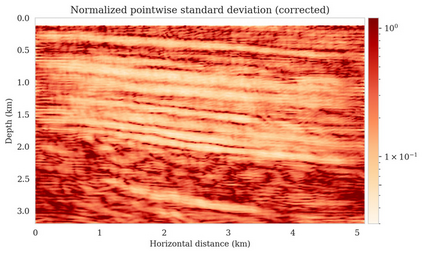
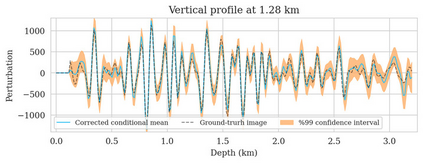
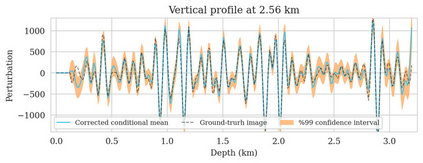
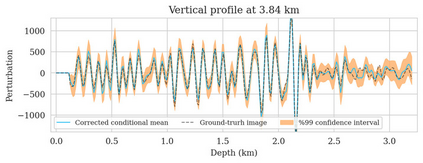
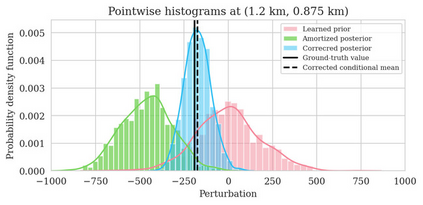
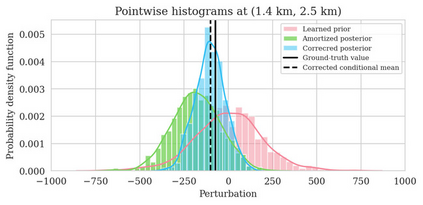
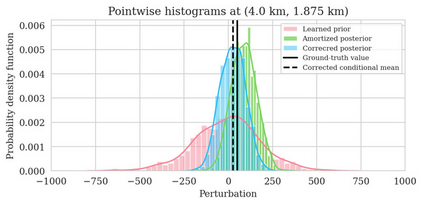
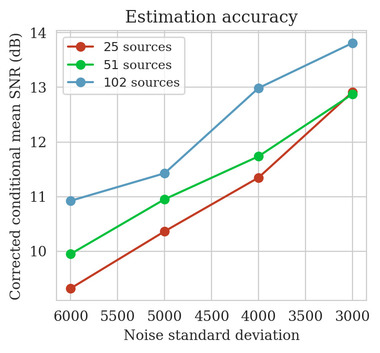
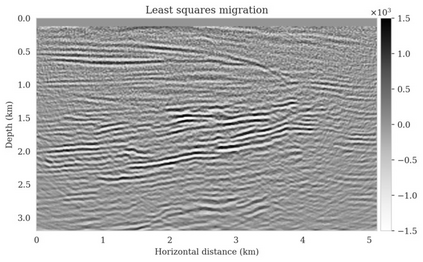
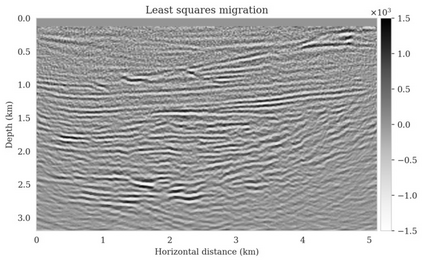
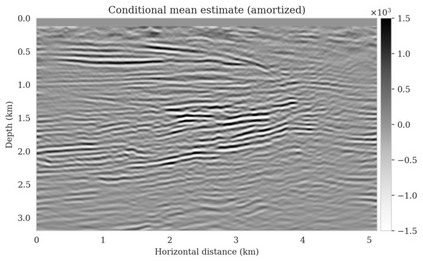
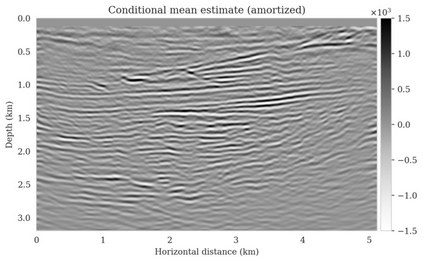
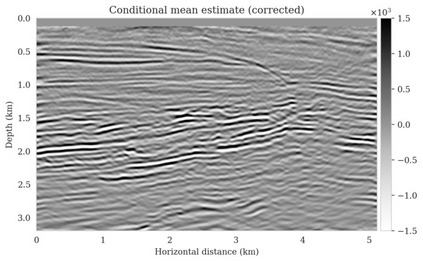
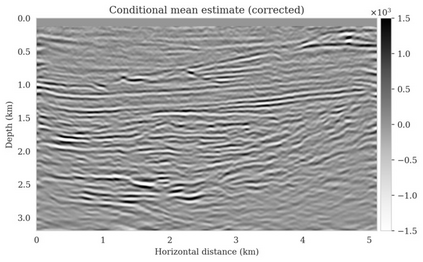
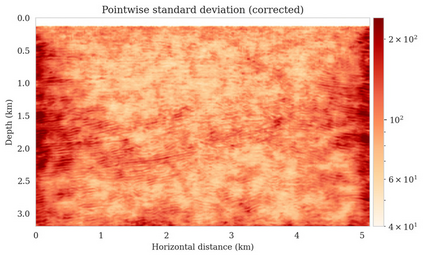
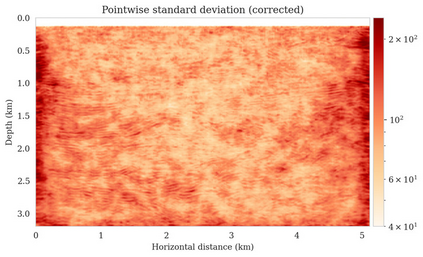
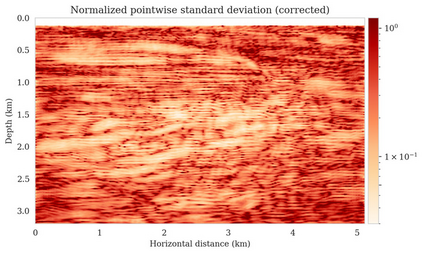
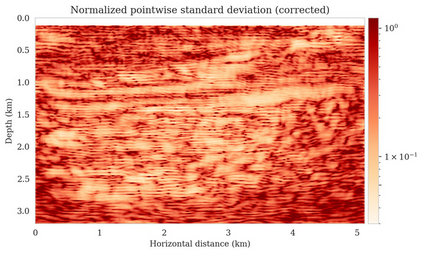
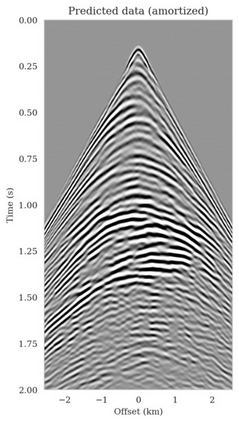
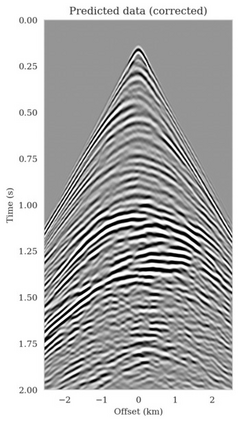
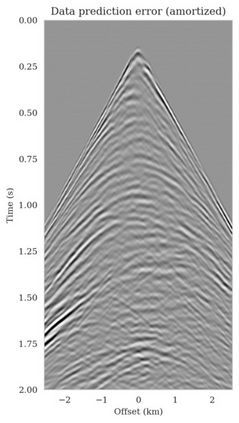
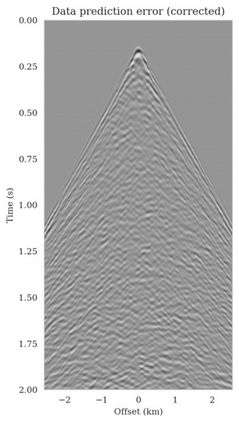
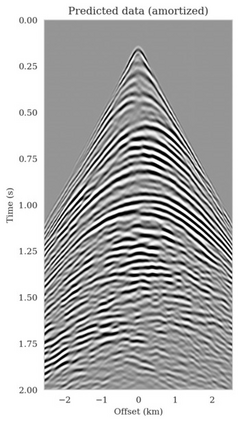
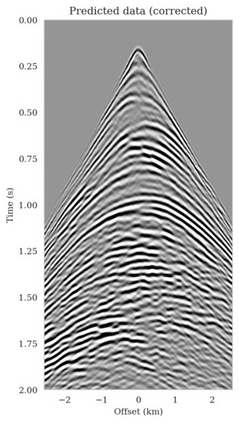
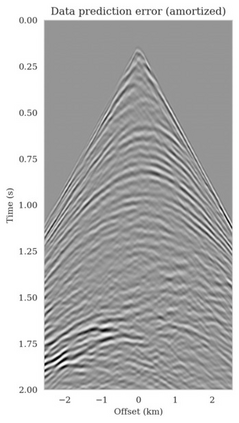
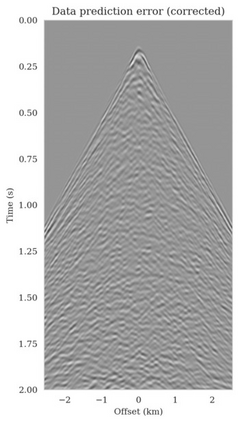
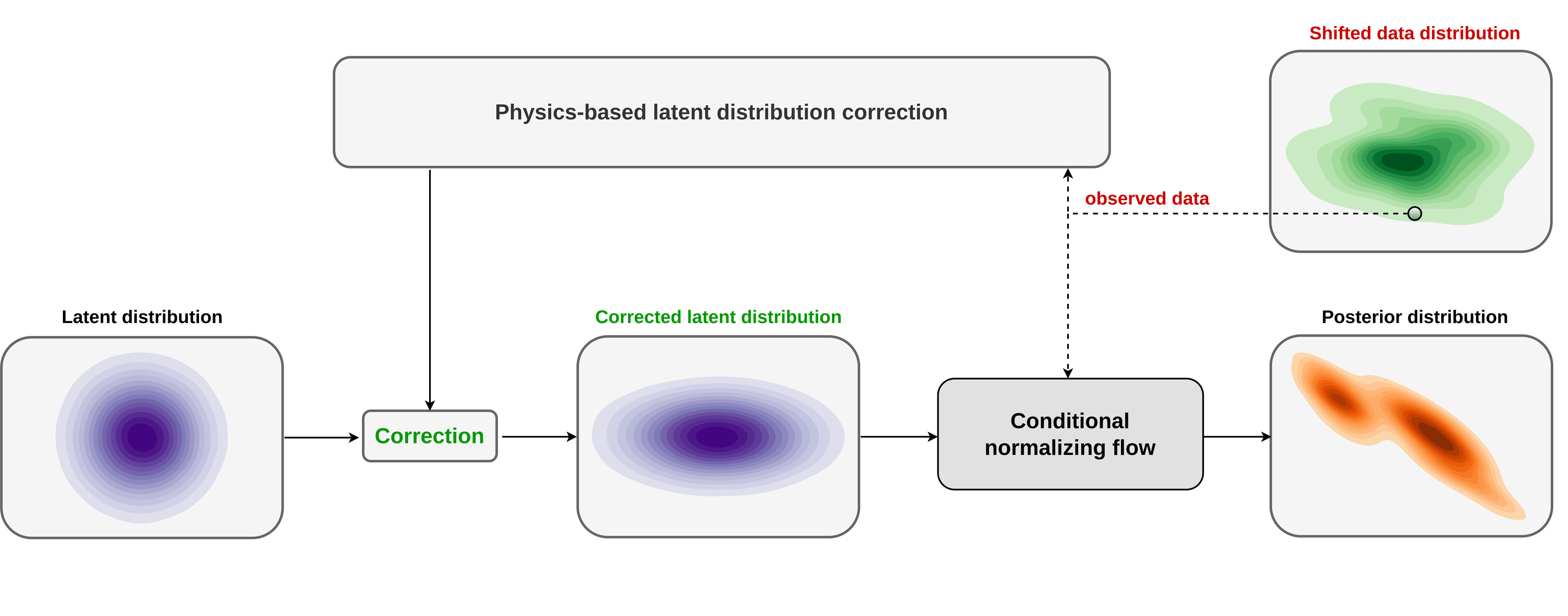
Bayesian inference for high-dimensional inverse problems is computationally costly and requires selecting a suitable prior distribution. Amortized variational inference addresses these challenges via a neural network that approximates the posterior distribution not only for one instance of data, but a distribution of data pertaining to a specific inverse problem. During inference, the neural network -- in our case a conditional normalizing flow -- provides posterior samples at virtually no cost. However, the accuracy of amortized variational inference relies on the availability of high-fidelity training data, which seldom exists in geophysical inverse problems due to the Earth's heterogeneity. In addition, the network is prone to errors if evaluated over out-of-distribution data. As such, we propose to increase the resilience of amortized variational inference in the presence of moderate data distribution shifts. We achieve this via a correction to the latent distribution that improves the posterior distribution approximation for the data at hand. The correction involves relaxing the standard Gaussian assumption on the latent distribution and parameterizing it via a Gaussian distribution with an unknown mean and (diagonal) covariance. These unknowns are then estimated by minimizing the Kullback-Leibler divergence between the corrected and the (physics-based) true posterior distributions. While generic and applicable to other inverse problems, by means of a linearized seismic imaging example, we show that our correction step improves the robustness of amortized variational inference with respect to changes in the number of seismic sources, noise variance, and shifts in the prior distribution. This approach provides a seismic image with limited artifacts and an assessment of its uncertainty at approximately the same cost as five reverse-time migrations.
翻译:高维反向问题的贝氏推论是计算成本高昂的,需要选择适当的先前分布。 模拟变异推论通过神经网络应对这些挑战,该神经网络不仅对某一类数据近似后端分布,而且对与特定反问题有关的数据分布进行近似。在推断过程中,神经网络 -- -- 就我们而言,是有条件的正常流流 -- -- 提供了后部样本,但几乎不花费费用。然而,摊合变异推论的准确性取决于能否得到高易变性培训数据,这些数据很少存在于地球物理的反常问题中,由于地球的稳健度变化造成的地球物理反常问题中。此外,如果对后部分布进行评估,这个网络很容易出错。因此,我们提议在存在中度数据分布变化时,通过修正来提高振动变异性变异性变异性反应的弹性,通过高空变异性变异性变异性变异性变异性变异性变异性变异性变异性变异性变异性变异性变异性变异性变异性变异性变异性变异性变异性变异性变异性变异性变异性变异性变性变异性变异性变异性变异性变异性变异性变异性变异性变异性变异性变异性变异性变异性变异性变异性变异性变性变异性变异性变异性变性变性变异性变异性变性变性变性变性变性变性变性变性变异性变异性变性变异性变性变性变性变性变性变性变性变性变异性变异性变异性变性变性变性变性变性变性变性变性变性变性变性变异性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变