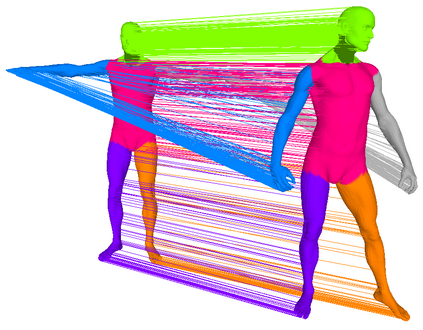
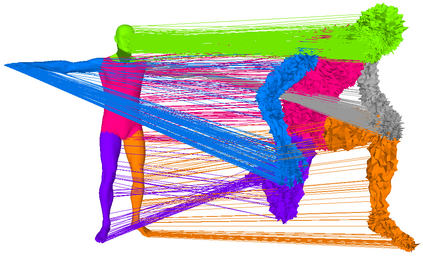
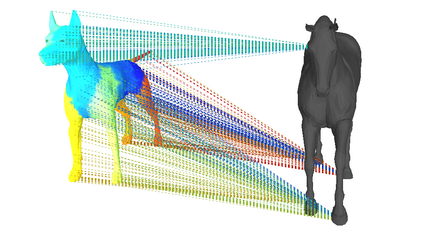
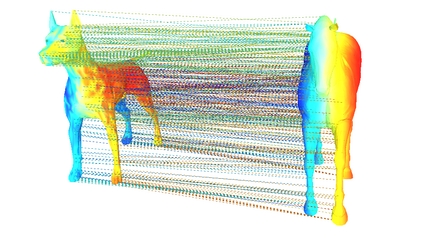
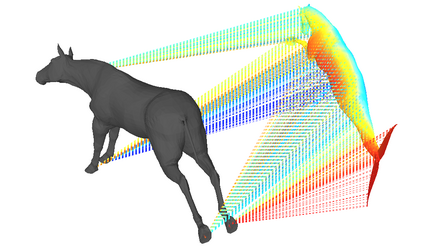
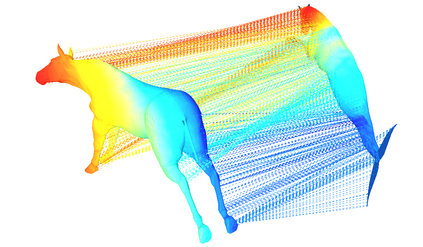
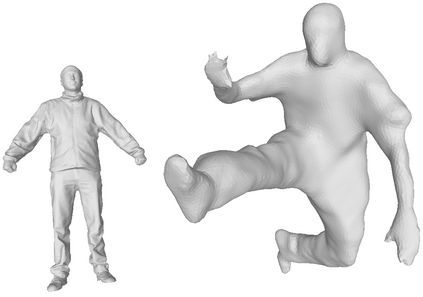
We address the problem of 3D shape registration and we propose a novel technique based on spectral graph theory and probabilistic matching. The task of 3D shape analysis involves tracking, recognition, registration, etc. Analyzing 3D data in a single framework is still a challenging task considering the large variability of the data gathered with different acquisition devices. 3D shape registration is one such challenging shape analysis task. The main contribution of this chapter is to extend the spectral graph matching methods to very large graphs by combining spectral graph matching with Laplacian embedding. Since the embedded representation of a graph is obtained by dimensionality reduction we claim that the existing spectral-based methods are not easily applicable. We discuss solutions for the exact and inexact graph isomorphism problems and recall the main spectral properties of the combinatorial graph Laplacian; We provide a novel analysis of the commute-time embedding that allows us to interpret the latter in terms of the PCA of a graph, and to select the appropriate dimension of the associated embedded metric space; We derive a unit hyper-sphere normalization for the commute-time embedding that allows us to register two shapes with different samplings; We propose a novel method to find the eigenvalue-eigenvector ordering and the eigenvector signs using the eigensignature (histogram) which is invariant to the isometric shape deformations and fits well in the spectral graph matching framework, and we present a probabilistic shape matching formulation using an expectation maximization point registration algorithm which alternates between aligning the eigenbases and finding a vertex-to-vertex assignment.
翻译:我们处理 3D 形状注册问题, 我们提出基于光谱图形理论和概率匹配的新技术 。 3D 形状分析的任务涉及跟踪、 识别、 注册等等 。 在一个单一框架中分析 3D 数据仍然是一项艰巨的任务。 考虑到以不同购置设备收集的数据差异很大。 3D 形状注册是一项具有挑战性的形状分析任务 。 本章的主要贡献是通过将光谱图与 Laplacian 嵌入式相匹配, 将光谱图匹配方法扩大到非常大的图表 。 由于一个图表的嵌入式表达方式是通过维度减少获得的。 我们声称, 现有的光谱基结构分析方法不易适用 。 我们讨论精确和不精确的图形异形化问题的解决办法, 并且回顾调色图的主要光谱特性 。 我们对通勤时间嵌入的嵌入方式进行了新分析, 使我们能够从一个图形的固定值的角度来解释后者, 并选择相关的直径直径匹配空间的适当维度; 我们从一个单位的透视频率递增的直径正常度框架 。