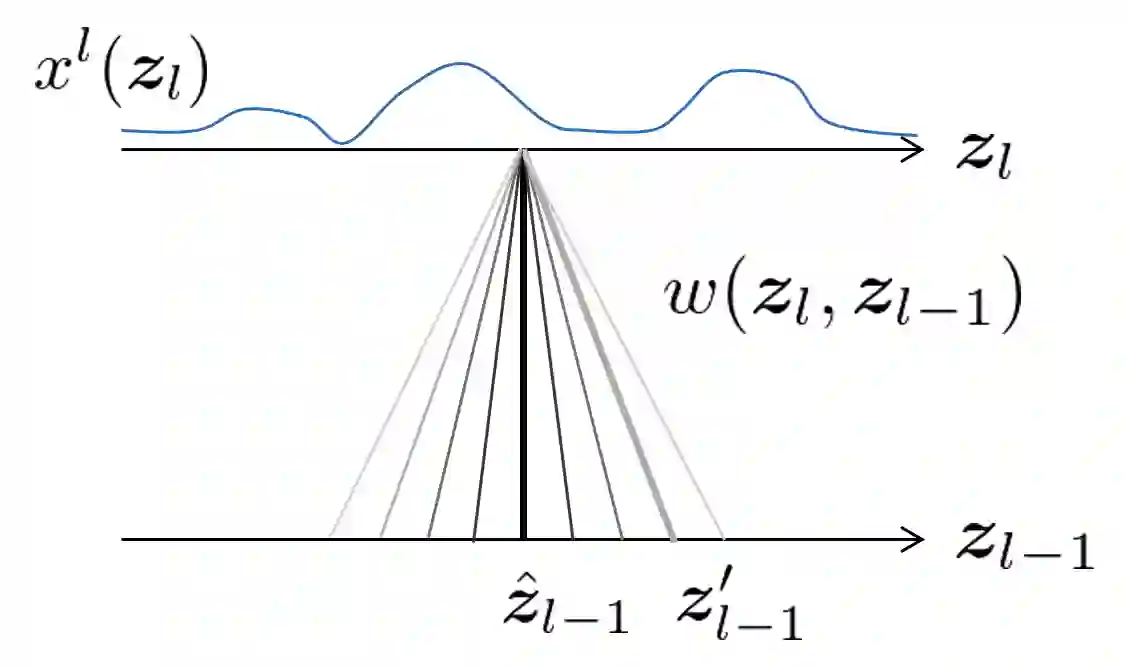
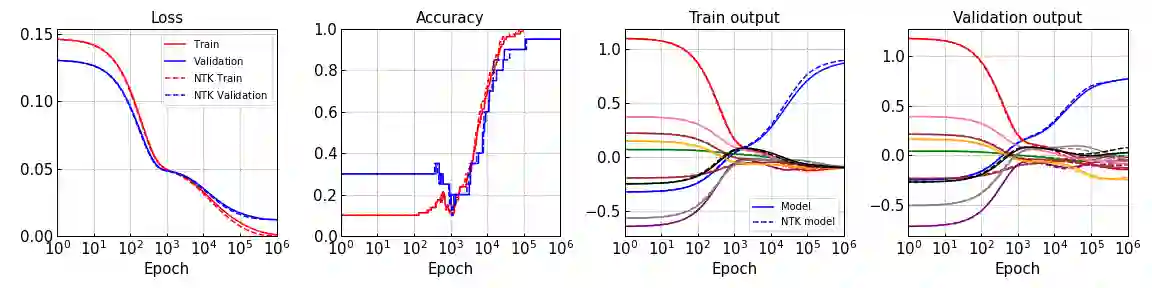
A biological neural network in the cortex forms a neural field. Neurons in the field have their own receptive fields, and connection weights between two neurons are random but highly correlated when they are in close proximity in receptive fields. In this paper, we investigate such neural fields in a multilayer architecture to investigate the supervised learning of the fields. We empirically compare the performances of our field model with those of randomly connected deep networks. The behavior of a randomly connected network is investigated on the basis of the key idea of the neural tangent kernel regime, a recent development in the machine learning theory of over-parameterized networks; for most randomly connected neural networks, it is shown that global minima always exist in their small neighborhoods. We numerically show that this claim also holds for our neural fields. In more detail, our model has two structures: i) each neuron in a field has a continuously distributed receptive field, and ii) the initial connection weights are random but not independent, having correlations when the positions of neurons are close in each layer. We show that such a multilayer neural field is more robust than conventional models when input patterns are deformed by noise disturbances. Moreover, its generalization ability can be slightly superior to that of conventional models.
翻译:皮层中的生物神经网络形成神经场。 实地的神经神经网络有其自身的可接受字段, 两个神经神经元之间的连接重量在接近可接受字段时是随机的, 但高度相关。 在本文中, 我们在一个多层结构中调查这些神经领域, 以调查受监督的田间学习情况。 我们用经验比较了我们田间模型的性能和随机连接的深层网络的性能。 随机连接网络的行为是根据神经核内核系统的关键概念来调查的, 这是超分数网络机器学习理论的最新发展; 对于最随机连接的神经网络来说, 显示全球微型神经系统总是存在于小的邻里。 我们用数字来显示, 这一主张也存在于我们的神经领域。 更详尽地说, 我们的模型有两个结构 : (一) 每个田间神经元有一个持续分布的可接受字段, 以及 (二) 初始连接重量是随机的, 但并不独立, 当神经元的位置接近每一层时, 即机器的机器学习理论最近的发展; 对于最随机的神经网络网络来说, 这种多层次的模型是比常规的模型更牢固的。 。 。 当常规的神经模型比常规的模型更稳定的模型更稳定的模型更稳定时, 。