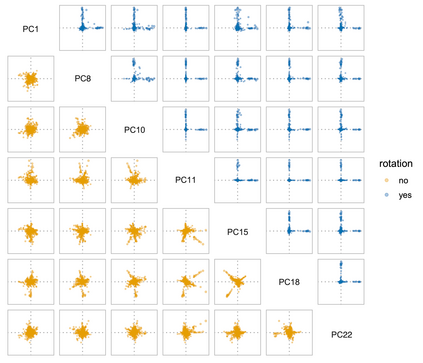
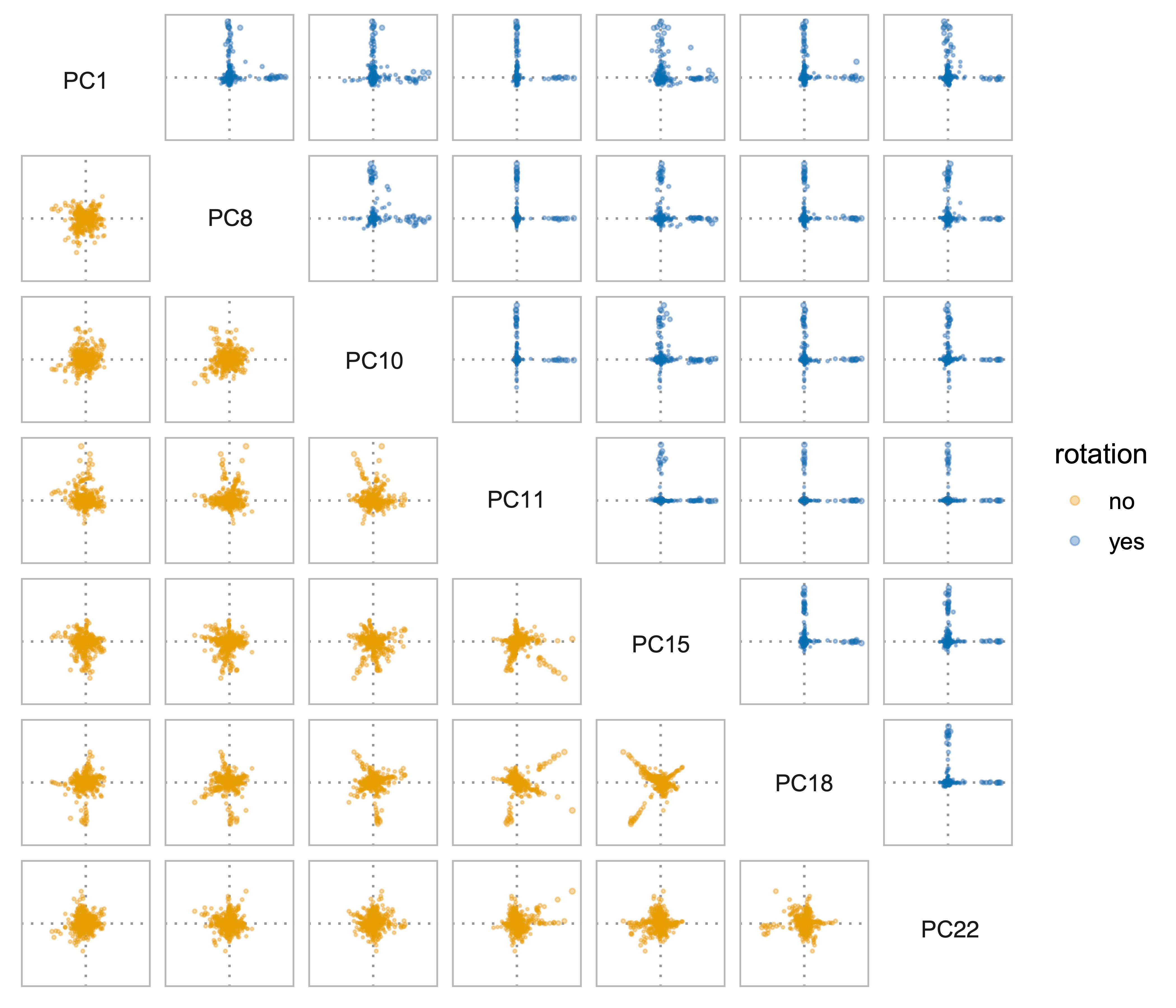
Previous versions of sparse principal component analysis (PCA) have presumed that the eigen-basis (a $p \times k$ matrix) is approximately sparse. We propose a method that presumes the $p \times k$ matrix becomes approximately sparse after a $k \times k$ rotation. The simplest version of the algorithm initializes with the leading $k$ principal components. Then, the principal components are rotated with an $k \times k$ orthogonal rotation to make them approximately sparse. Finally, soft-thresholding is applied to the rotated principal components. This approach differs from prior approaches because it uses an orthogonal rotation to approximate a sparse basis. One consequence is that a sparse component need not to be a leading eigenvector, but rather a mixture of them. In this way, we propose a new (rotated) basis for sparse PCA. In addition, our approach avoids "deflation" and multiple tuning parameters required for that. Our sparse PCA framework is versatile; for example, it extends naturally to a two-way analysis of a data matrix for simultaneous dimensionality reduction of rows and columns. We provide evidence showing that for the same level of sparsity, the proposed sparse PCA method is more stable and can explain more variance compared to alternative methods. Through three applications -- sparse coding of images, analysis of transcriptome sequencing data, and large-scale clustering of social networks, we demonstrate the modern usefulness of sparse PCA in exploring multivariate data.
翻译:原始元件分析( PCA) 以前版本的原始元件分析( PCA ) 的旋转假设 eigen- basis ( $p $\ times k$ 矩阵) 大约是很少的 。 我们提出一种方法, 假设美元= time k$ 旋转后, 美元= time k$ k$ 旋转后, 基质分析( PCA) 基质分析( PCA ) 将原始元件的原始版本旋转。 然后, 主要元件会以美元\ time k$ k$ orthogon 旋转后, 假设 egen- pal- production 和 mission roadal roduction 工具的软盘化方法。 一种稀释组件的稀释方法可以避免“ 衰减” 和 多调值参数 。 我们稀释的 CPA 框架是多功能化的, 例如, 它会自然扩展到先前的方法, 因为它使用正统旋转的网络旋转旋转, 接近于稀释的旋转旋转旋转 基旋转 基质旋转 基 基 基 基图 基数 基数 。 一个比 数据 解 数据 解 解, 我们为 的 解 解 的 的 的 的 解算 的 的 的 的 的 的 的 的 基数 基数 解 的 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 度 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解 解