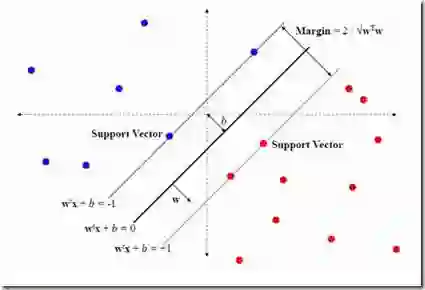
The support vector machine (SVM) and minimum Euclidean norm least squares regression are two fundamentally different approaches to fitting linear models, but they have recently been connected in models for very high-dimensional data through a phenomenon of support vector proliferation, where every training example used to fit an SVM becomes a support vector. In this paper, we explore the generality of this phenomenon and make the following contributions. First, we prove a super-linear lower bound on the dimension (in terms of sample size) required for support vector proliferation in independent feature models, matching the upper bounds from previous works. We further identify a sharp phase transition in Gaussian feature models, bound the width of this transition, and give experimental support for its universality. Finally, we hypothesize that this phase transition occurs only in much higher-dimensional settings in the $\ell_1$ variant of the SVM, and we present a new geometric characterization of the problem that may elucidate this phenomenon for the general $\ell_p$ case.
翻译:支持矢量机(SVM)和最小的 Euclidean 规范最小平方回归是两种根本不同的方法,可以对线性模型进行匹配,但是它们最近通过支持矢量扩散的现象在非常高的维度数据模型中被连接起来,其中用于适应 SVM 的每一个培训范例都成为支持矢量扩散的矢量扩散。在本文中,我们探讨了这一现象的普遍性,并做出了以下贡献。首先,我们证明在独立特性模型中支持矢量扩散所需的尺寸(样本大小)上下行的线性约束,与以前作品的上界相匹配。我们进一步确定了高斯特征模型的尖锐阶段过渡,将这一过渡的宽度捆绑起来,并为其普遍性提供实验性支持。最后,我们假设这一阶段的过渡仅在SVM $\ell_1美元变量中的高度环境中发生,我们为一般的 $\ell_p$案例展示了对问题进行解释的新几何特征定性。