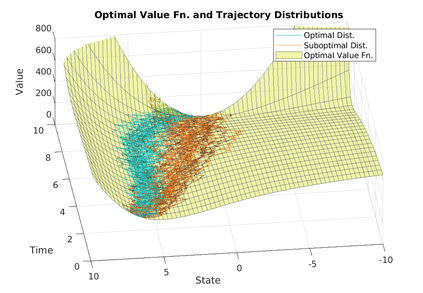
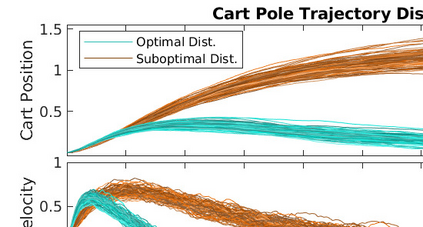
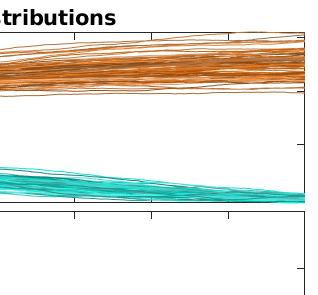
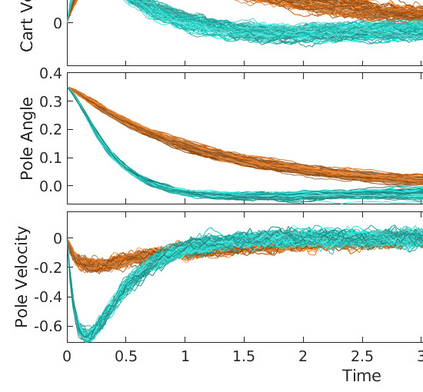
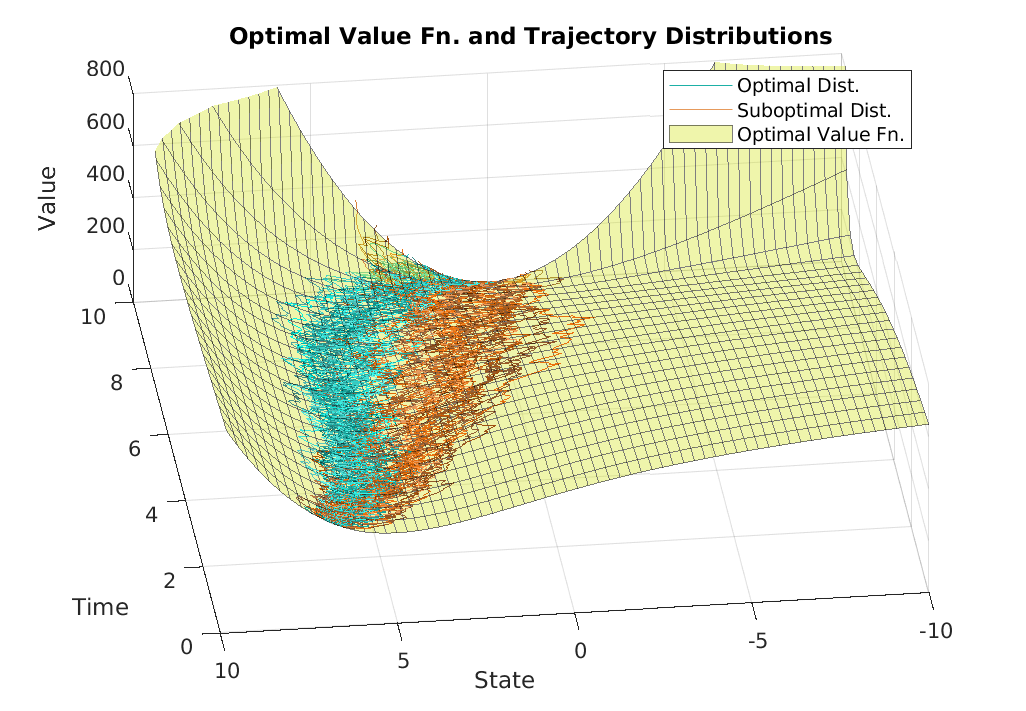
Two novel numerical estimators are proposed for solving forward-backward stochastic differential equations (FBSDEs) appearing in the Feynman-Kac representation of the value function in stochastic optimal control problems. In contrast to the current numerical approaches which are based on the discretization of the continuous-time FBSDE, we propose a converse approach, namely, we obtain a discrete-time approximation of the on-policy value function, and then we derive a discrete-time estimator that resembles the continuous-time counterpart. The proposed approach allows for the construction of higher accuracy estimators along with error analysis. The approach is applied to the policy improvement step in reinforcement learning. Numerical results and error analysis are demonstrated using (i) a scalar nonlinear stochastic optimal control problem and (ii) a four-dimensional linear quadratic regulator (LQR) problem. The proposed estimators show significant improvement in terms of accuracy in both cases over Euler-Maruyama-based estimators used in competing approaches. In the case of LQR problems, we demonstrate that our estimators result in near machine-precision level accuracy, in contrast to previously proposed methods that can potentially diverge on the same problems.
翻译:为了解决Feynman-Kac中出现的在随机最佳控制问题中价值函数代表的Feynman-Kac中出现的向后随机随机差异方程式(FBSDEs),提出了两个新的数字估计器。与目前基于连续时间FBSDE的离散数字方法相反,我们提议了一个反向方法,即我们获得政策值函数的离散时间近似值,然后我们得出一个类似于连续时间对应方的离散时间估计器。拟议方法允许在进行错误分析的同时构建更高的准确度估计器。该方法适用于加强学习的政策改进步骤。数字结果和误差分析是用以下方法进行的:(一) 星际非线性非线性随机最佳控制问题,和(二) 四维线性梯度调控管(LQR) 问题。拟议的估计器显示,在两种情况中,与Euler-Mariya基的测算器相比,精确度都有很大改进。在近Qrcisiro 级方法中,我们用不同的方法显示,我们之前的测算方法可能存在同样的问题。