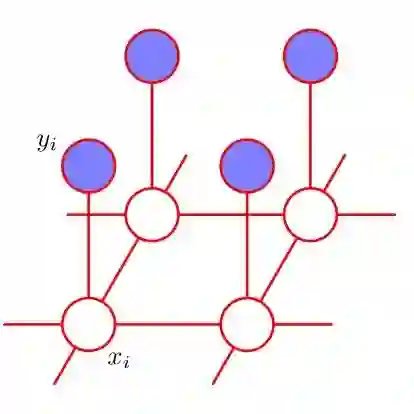
Performing a Bayesian inference on large spatio-temporal models requires extracting inverse elements of large sparse precision matrices for marginal variances. Although direct matrix factorizations can be used for the inversion, such methods fail to scale well for distributed problems when run on large computing clusters. On the contrary, Krylov subspace methods for the selected inversion have been gaining traction. We propose a parallel hybrid approach based on domain decomposition, which extends the Rao-Blackwellized Monte Carlo estimator for distributed precision matrices. Our approach exploits the strength of Krylov subspace methods as global solvers and efficiency of direct factorizations as base case solvers to compute the marginal variances using a divide-and-conquer strategy. By introducing subdomain overlaps, one can achieve a greater accuracy at an increased computational effort with little to no additional communication. We demonstrate the speed improvements on both simulated models and a massive US daily temperature data.
翻译:暂无翻译