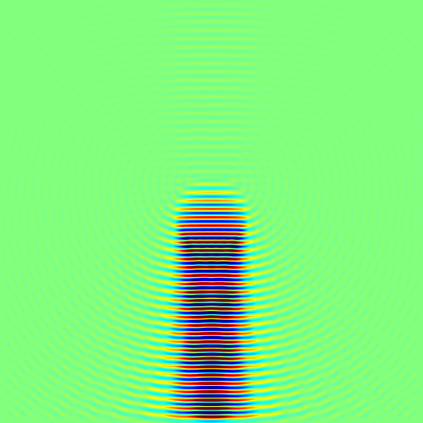
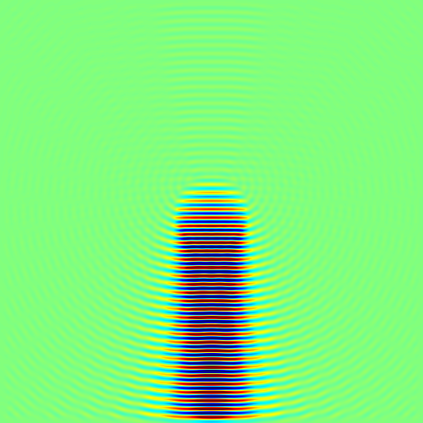
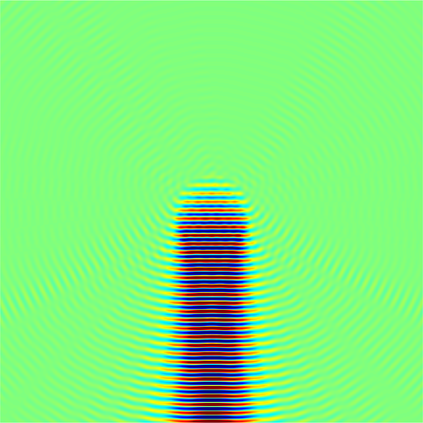
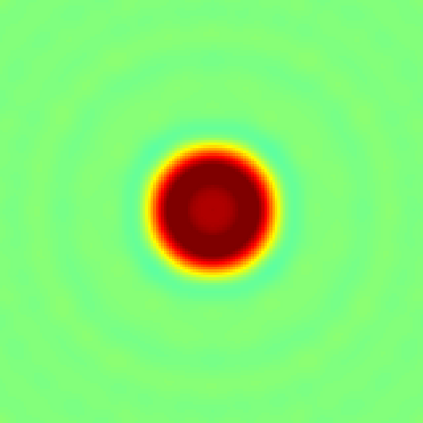
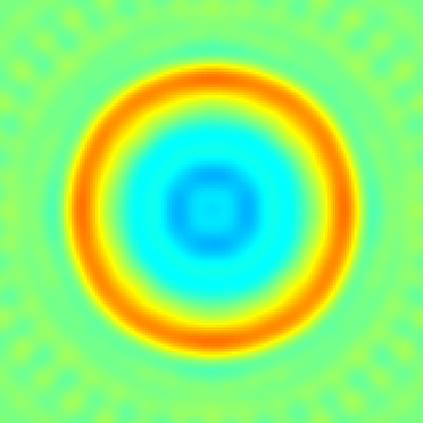
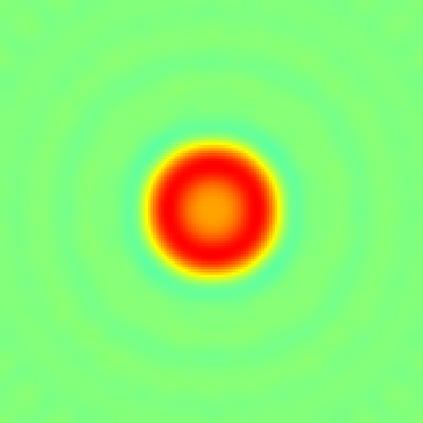
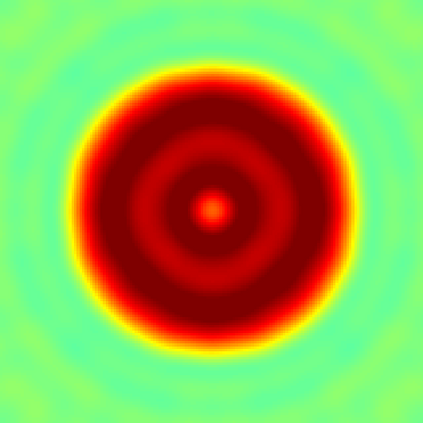
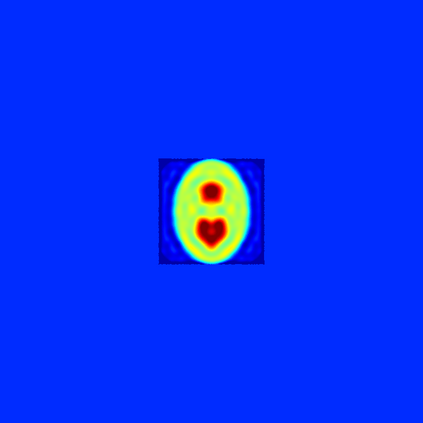
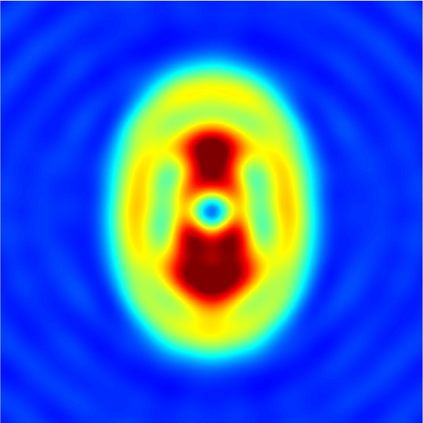
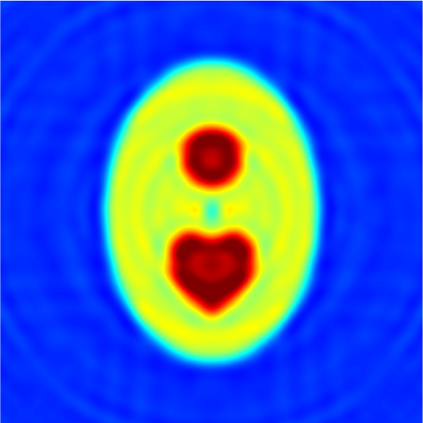
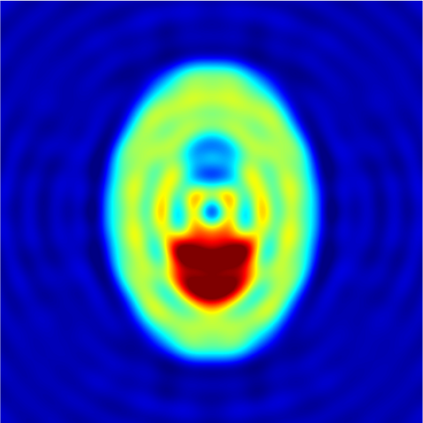
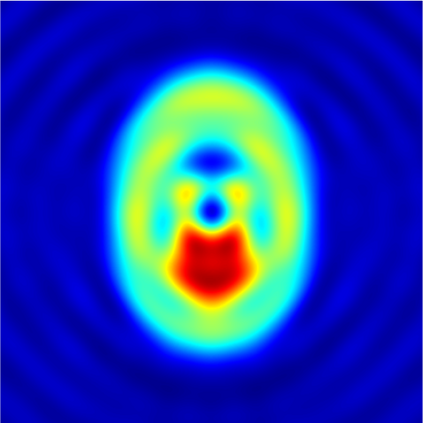
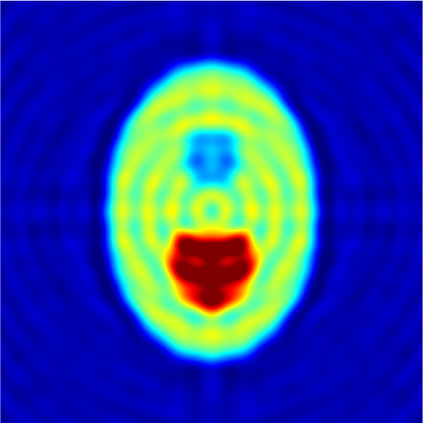
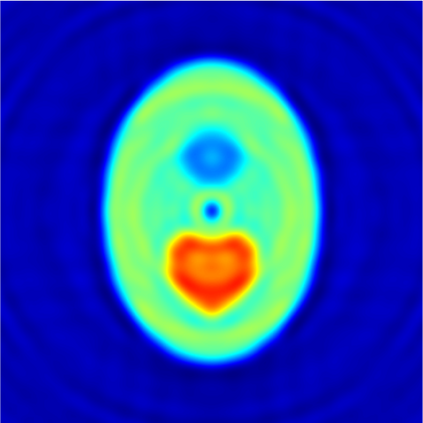
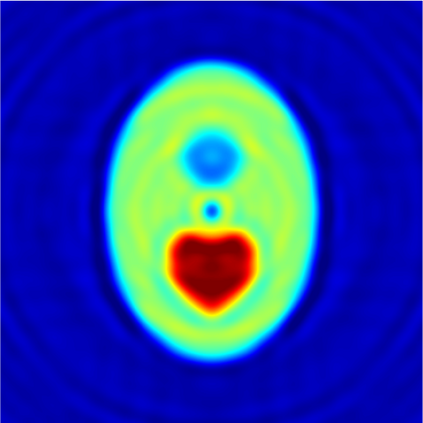
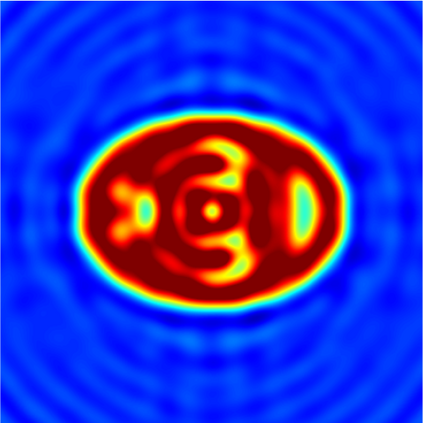
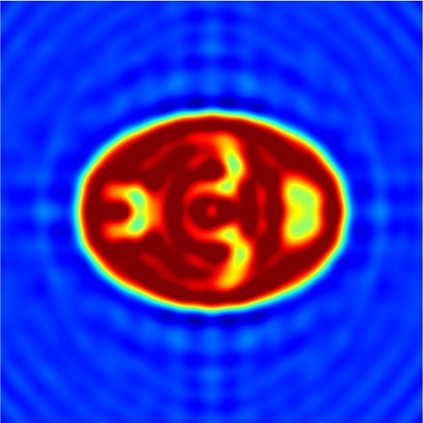
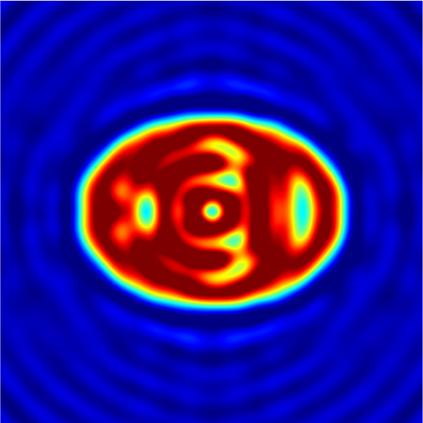
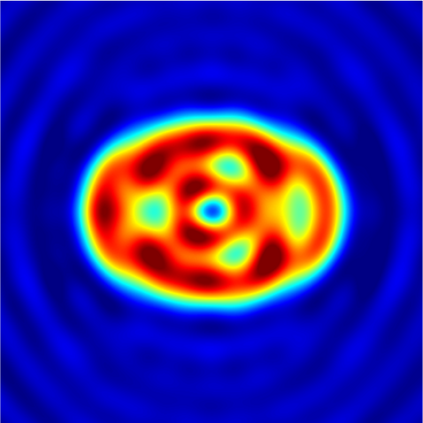
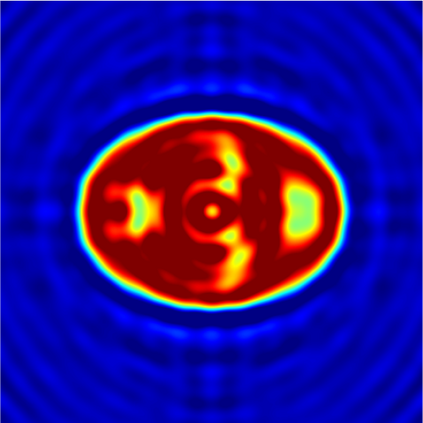
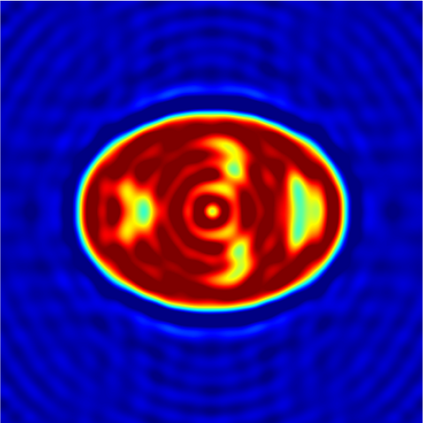
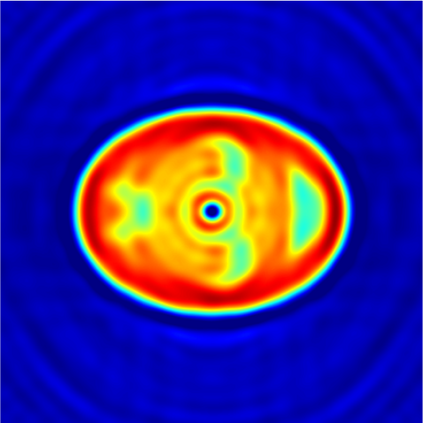
In this paper, we study the mathematical imaging problem of diffraction tomography (DT), which is an inverse scattering technique used to find material properties of an object by illuminating it with probing waves and recording the scattered waves. Conventional DT relies on the Fourier diffraction theorem, which is applicable under the condition of weak scattering. However, if the object has high contrasts or is too large compared to the wavelength, it tends to produce multiple scattering, which complicates the reconstruction. We give a survey on diffraction tomography and compare the reconstruction of low and high contrast objects. We also implement and compare the reconstruction using the full waveform inversion method which, contrary to the Born and Rytov approximations, works with the total field and is more robust to multiple scattering.
翻译:在本文中,我们研究了碎片成像(DT)的数学成像问题,这是一种反向散射技术,用来通过用探测波和记录散落波来发现物体的物质特性。常规DT依靠Fourier difrection 定律,该定律在微弱散射条件下适用。但是,如果对象的反差或与波长相比太大,则往往产生多种散射,使重建复杂化。我们进行了关于碎片成像的调查,比较了低和高反差物体的重建情况。我们还采用与Born和Rytov近似相反的全波形反向法来实施和比较重建情况,这种方法与Born和Rytov近似,它与整个场相对应,而且对多散射更为有力。