GIPA++: A General Information Propagation Algorithm for Graph Learning

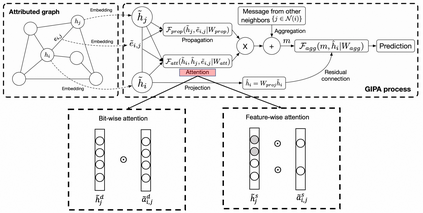
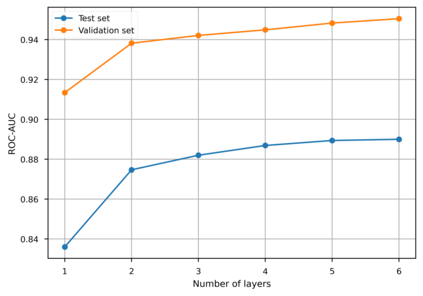
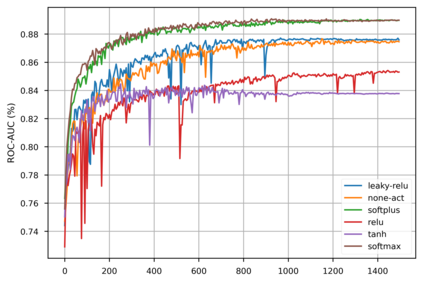
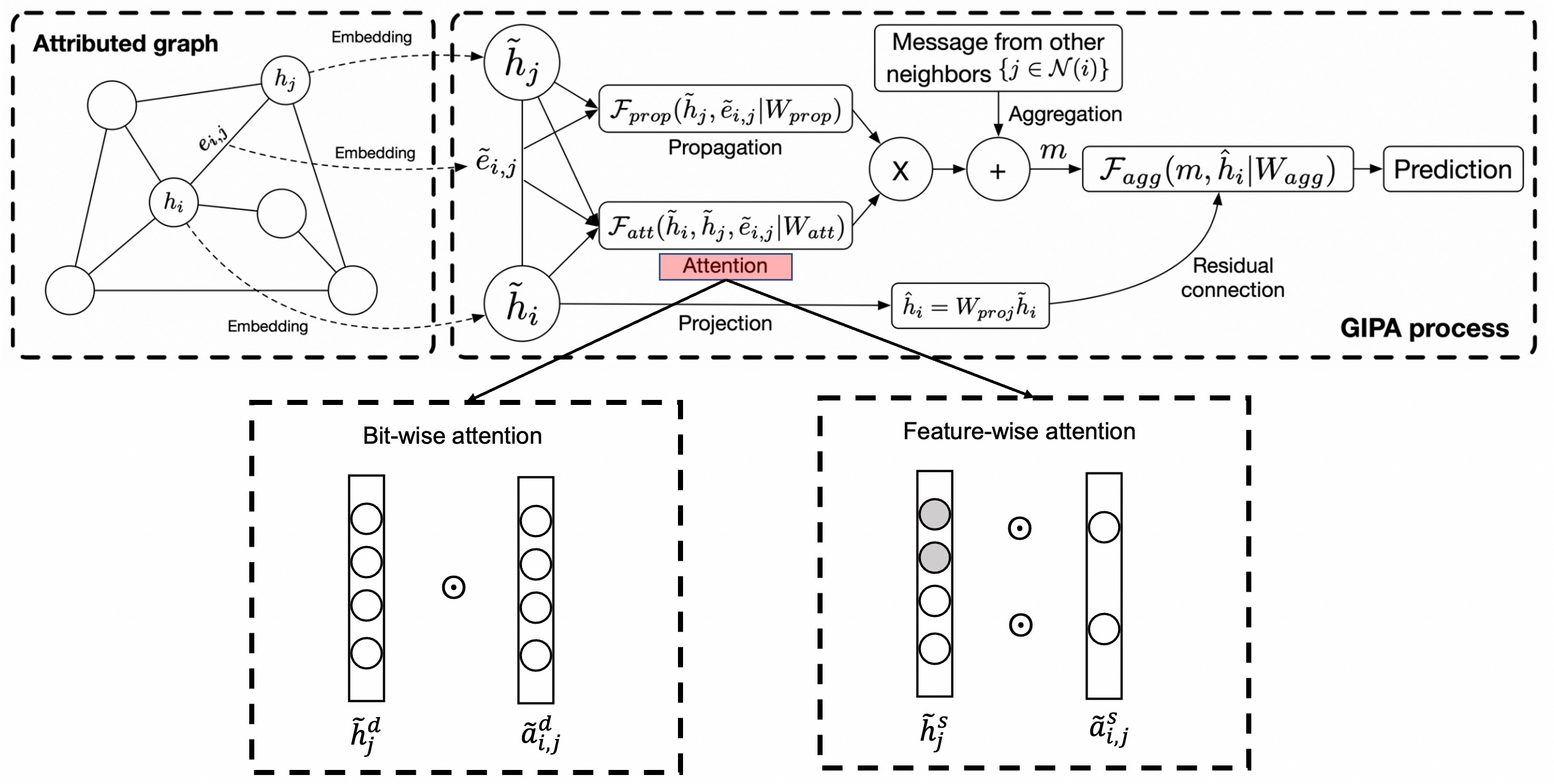
Graph neural networks (GNNs) have been widely used in graph-structured data computation, showing promising performance in various applications such as node classification, link prediction, and network recommendation. Existing works mainly focus on node-wise correlation when doing weighted aggregation of neighboring nodes based on attention, such as dot product by the dense vectors of two nodes. This may cause conflicting noise in nodes to be propagated when doing information propagation. To solve this problem, we propose a General Information Propagation Algorithm (GIPA in short), which exploits more fine-grained information fusion including bit-wise and feature-wise correlations based on edge features in their propagation. Specifically, the bit-wise correlation calculates the element-wise attention weight through a multi-layer perceptron (MLP) based on the dense representations of two nodes and their edge; The feature-wise correlation is based on the one-hot representations of node attribute features for feature selection. We evaluate the performance of GIPA on the Open Graph Benchmark proteins (OGBN-proteins for short) dataset and the Alipay dataset of Alibaba. Experimental results reveal that GIPA outperforms the state-of-the-art models in terms of prediction accuracy, e.g., GIPA achieves an average ROC-AUC of $0.8901\pm 0.0011$, which is better than that of all the existing methods listed in the OGBN-proteins leaderboard.