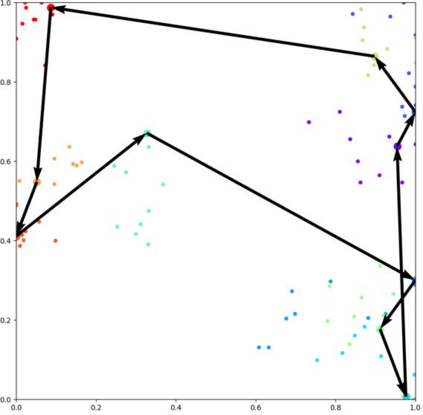
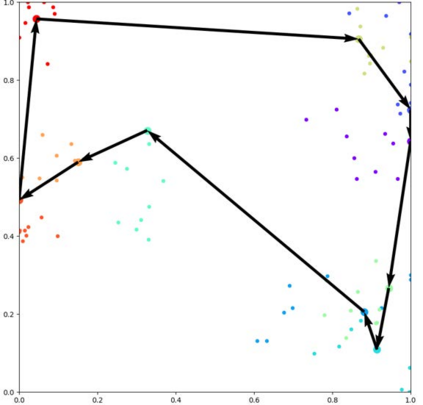
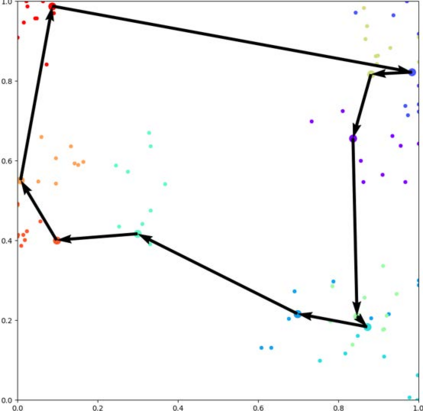
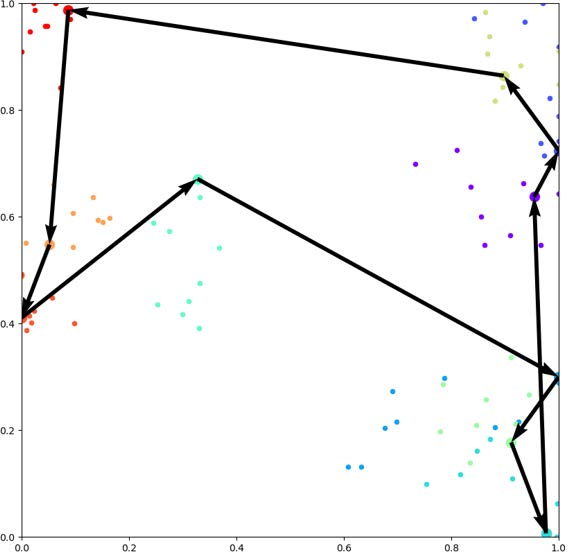
Graph problems such as traveling salesman problem, or finding minimal Steiner trees are widely studied and used in data engineering and computer science. Typically, in real-world applications, the features of the graph tend to change over time, thus, finding a solution to the problem becomes challenging. The dynamic version of many graph problems are the key for a plethora of real-world problems in transportation, telecommunication, and social networks. In recent years, using deep learning techniques to find heuristic solutions for NP-hard graph combinatorial problems has gained much interest as these learned heuristics can find near-optimal solutions efficiently. However, most of the existing methods for learning heuristics focus on static graph problems. The dynamic nature makes NP-hard graph problems much more challenging to learn, and the existing methods fail to find reasonable solutions. In this paper, we propose a novel architecture named Graph Temporal Attention with Reinforcement Learning (GTA-RL) to learn heuristic solutions for graph-based dynamic combinatorial optimization problems. The GTA-RL architecture consists of an encoder capable of embedding temporal features of a combinatorial problem instance and a decoder capable of dynamically focusing on the embedded features to find a solution to a given combinatorial problem instance. We then extend our architecture to learn heuristics for the real-time version of combinatorial optimization problems where all input features of a problem are not known a prior, but rather learned in real-time. Our experimental results against several state-of-the-art learning-based algorithms and optimal solvers demonstrate that our approach outperforms the state-of-the-art learning-based approaches in terms of effectiveness and optimal solvers in terms of efficiency on dynamic and real-time graph combinatorial optimization.
翻译:诸如旅行销售员问题或找到最起码的施泰纳树类等图表问题在数据工程和计算机科学中广泛研究和使用。 通常, 在现实世界应用中, 图表的特征往往会随着时间的变化而变化, 因此, 找到问题的解决方案会变得具有挑战性。 许多图表问题的动态版本是交通、 电信和社会网络中大量真实世界问题的关键。 近几年来, 利用深层次的学习技术为NP- 硬式图形组合问题寻找超常性解决方案, 这些学到的超常性格可以有效地找到近于最佳的解决方案 。 然而, 在现实世界应用中, 图表的特征往往会随着时间的变化而改变, 动态性能使得NP- 硬性图表问题更加难以解决, 而现有的方法无法找到合理的解决方案 。 在本文中, 我们提出一个名为“ 定时性关注” 结构, 来学习基于图形的动态组合优化优化优化优化方法的解决方案。 GTA-RL 结构包括一个能嵌化的时间特性, 用来将时间特性特性特性嵌入到我们之前的动态结构中 。