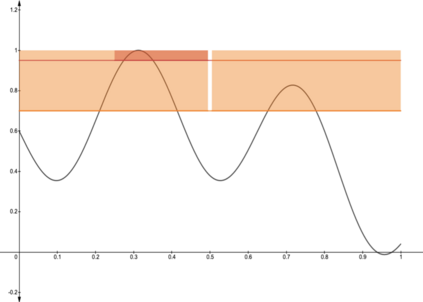
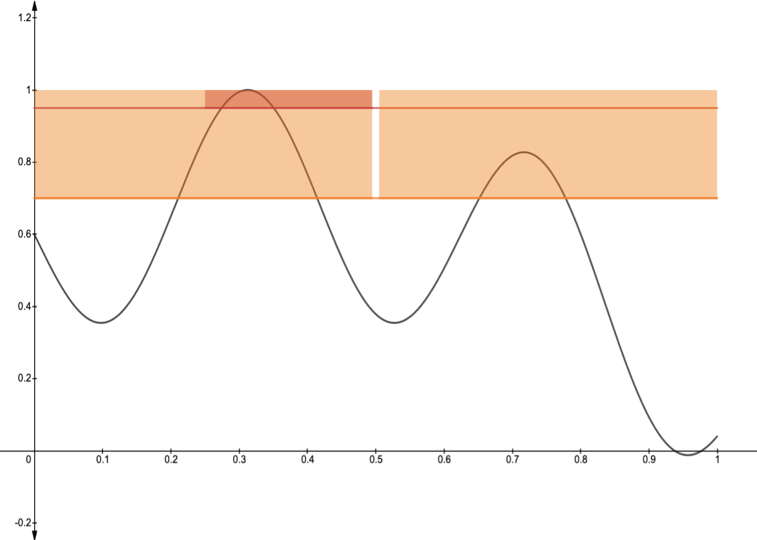
We consider sequential optimization of an unknown function in a reproducing kernel Hilbert space. We propose a Gaussian process-based algorithm and establish its order-optimal regret performance (up to a poly-logarithmic factor). This is the first GP-based algorithm with an order-optimal regret guarantee. The proposed algorithm is rooted in the methodology of domain shrinking realized through a sequence of tree-based region pruning and refining to concentrate queries in increasingly smaller high-performing regions of the function domain. The search for high-performing regions is localized and guided by an iterative estimation of the optimal function value to ensure both learning efficiency and computational efficiency. Compared with the prevailing GP-UCB family of algorithms, the proposed algorithm reduces computational complexity by a factor of $O(T^{2d-1})$ (where $T$ is the time horizon and $d$ the dimension of the function domain).
翻译:我们考虑在复制核心的Hilbert 空间时按顺序优化一个未知功能。 我们提出一个基于 Gaussian 的流程算法, 并确立其排序最佳的遗憾性能( 直至多对数系数 ) 。 这是第一个基于 GP 的算法, 且有排序最佳的遗憾性保证 。 提议的算法植根于通过基于树的区域排练和精炼序列实现的域缩小的方法, 以将查询集中在功能域中越来越小的高绩效区域 。 对高绩效区域的搜索是本地化的, 并遵循对最佳功能值的迭代估计, 以确保学习效率和计算效率。 与通用的 GP- UCB 算法组合相比, 提议的算法将计算复杂性降低到$O( T ⁇ 2d-1} ) ( 其中$T 是时间范围, $d美元是功能域的维度 ) 。