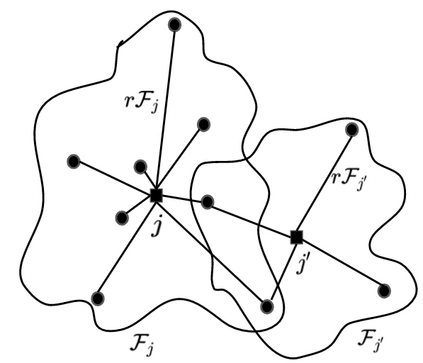
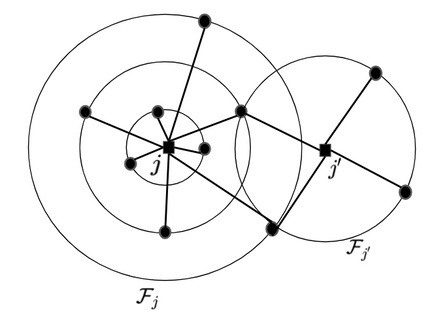
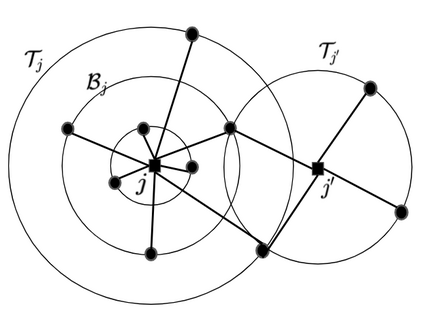
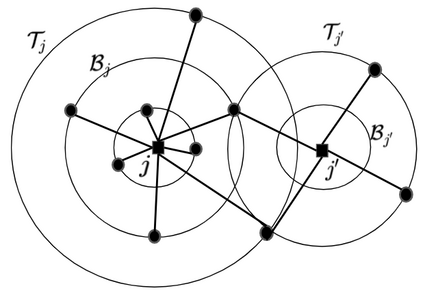
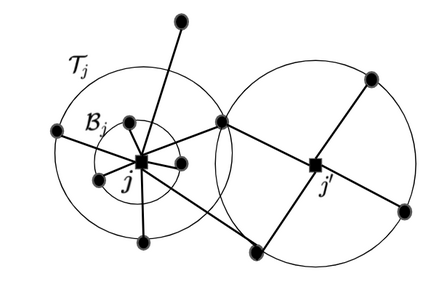
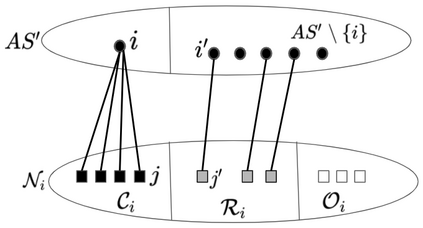
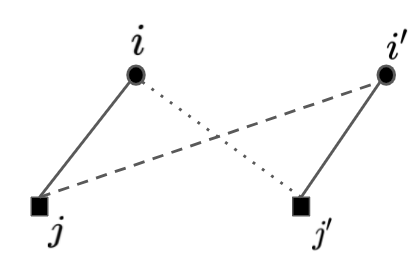
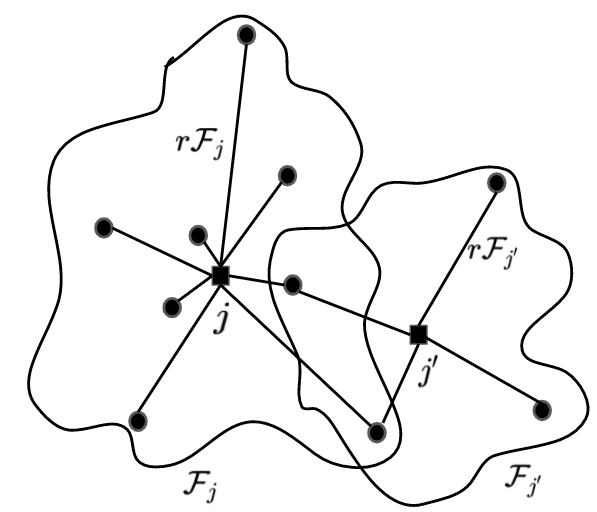
In this work, we study the extension of two variants of the facility location problem (FL) to make them robust towards a few distantly located clients. First, $k$-facility location problem ($k$FL), a common generalization of FL and $k$ median problems, is a well studied problem in literature. In the second variant, lower bounded facility location (LBFL), we are given a bound on the minimum number of clients that an opened facility must serve. Lower bounds are required in many applications like profitability in commerce and load balancing in transportation problem. In both the cases, the cost of the solution may be increased grossly by a few distantly located clients, called the outliers. Thus, in this work, we extend $k$FL and LBFL to make them robust towards the outliers. For $k$FL with outliers ($k$FLO) we present the first (constant) factor approximation violating the cardinality requirement by +1. As a by-product, we also obtain the first approximation for FLO based on LP-rounding. For LBFLO, we present a tri-criteria solution with a trade-off between the violations in lower bounds and the number of outliers. With a violation of $1/2$ in lower bounds, we get a violation of $2$ in outliers.
翻译:在这项工作中,我们研究了设施地点问题的两个变种的扩展,使其对几个远方客户具有强大的影响。首先,美元-设施问题(FL)的扩大,使其对几个远方客户具有强大的影响。首先,美元-设施地点问题(KFL)的问题(KFL),对FL和美元中位问题的共同概括,是文献中研究周密的一个问题。在第二个变种,即低约束设施地点(LFFFL),我们受开放设施必须服务的最低客户人数的约束。在许多应用中,如商业盈利和运输问题中负载平衡,要求降低界限。在这两种情况下,少数远方客户可能大大增加解决方案的成本,要求外端用户。因此,我们延长了美元-设施问题(KFLFL)和LFFL中位问题(KFFL)的范围,使之对外部用户产生强大的影响。我们提出了第一个(continent)因素的近似值,即违反基本要求+1.作为副产品,我们还获得了基于LP的FLO的首个近值,由几个远方客户(LFBFBILO)公司提出。我们提出一个低于1美元的违法的违反标准的数字。