From Zero-Freeness to Strong Spatial Mixing via a Christoffel-Darboux Type Identity

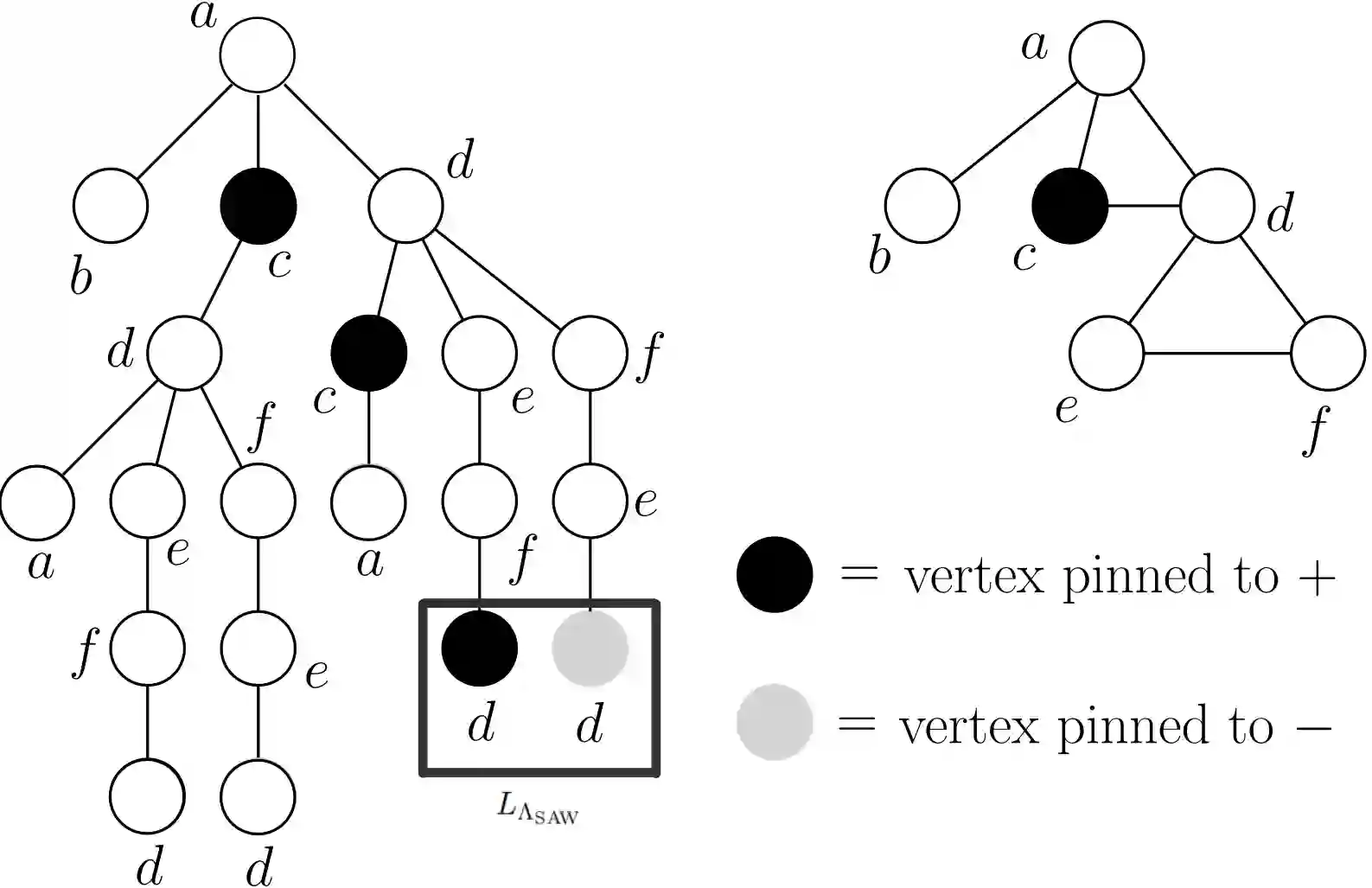
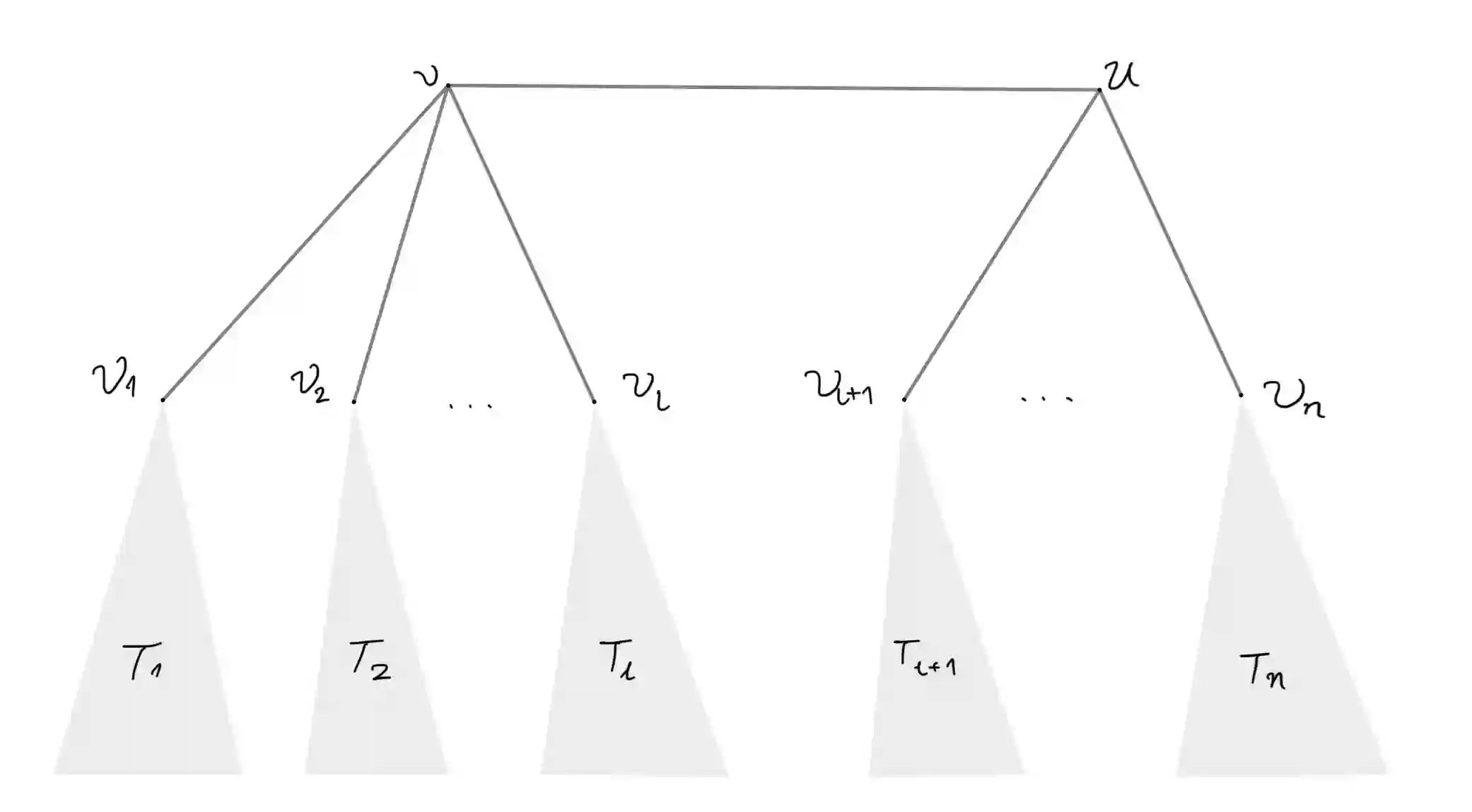
We derive the strong spatial mixing property for the general 2-spin system from zero-free regions of its partition function. We view the partition function of the 2-spin system as a multivariate function over three complex parameters $(\beta, \gamma, \lambda)$, and we allow the zero-free regions of $\beta, \gamma$ or $\lambda$ to be of arbitrary shapes. As long as the zero-free region contains a positive point and it is a complex neighborhood of $\lambda=0$ when fixing $\beta, \gamma \in \mathbb{C}$, or a complex neighborhood of $\beta\gamma=1$ when fixing $\beta, \lambda\in \mathbb{C}$ or $\gamma, \lambda\in \mathbb{C}$ respectively, we are able to show that the corresponding 2-spin system exhibits strong spatial mixing on such a region. The underlying graphs of the 2-spin system are not necessarily of bounded degree, while are required to include graphs with pinned vertices. We prove this result by establishing a Christoffel-Darboux type identity for the 2-spin system on trees and using certain tools from complex analysis. To our best knowledge, our result is general enough to turn all currently known zero-free regions of the partition function of the 2-spin system where pinned vertices are allowed into the strong spatial mixing property. Moreover, we extend our result to obtain strong spatial mixing for the ferromagnetic Ising model (even with non-uniform external fields) from the celebrated Lee-Yang circle theorem.