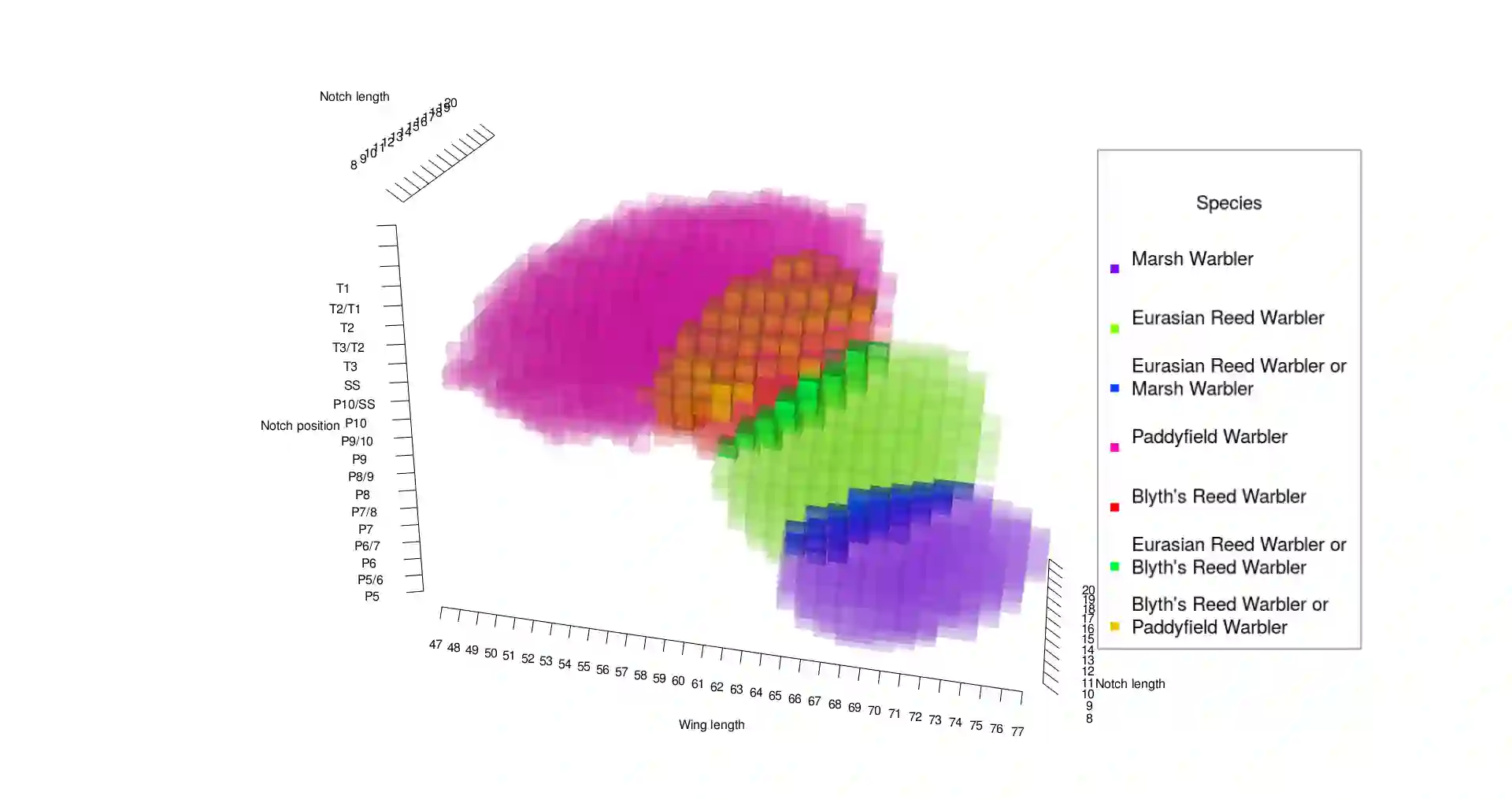
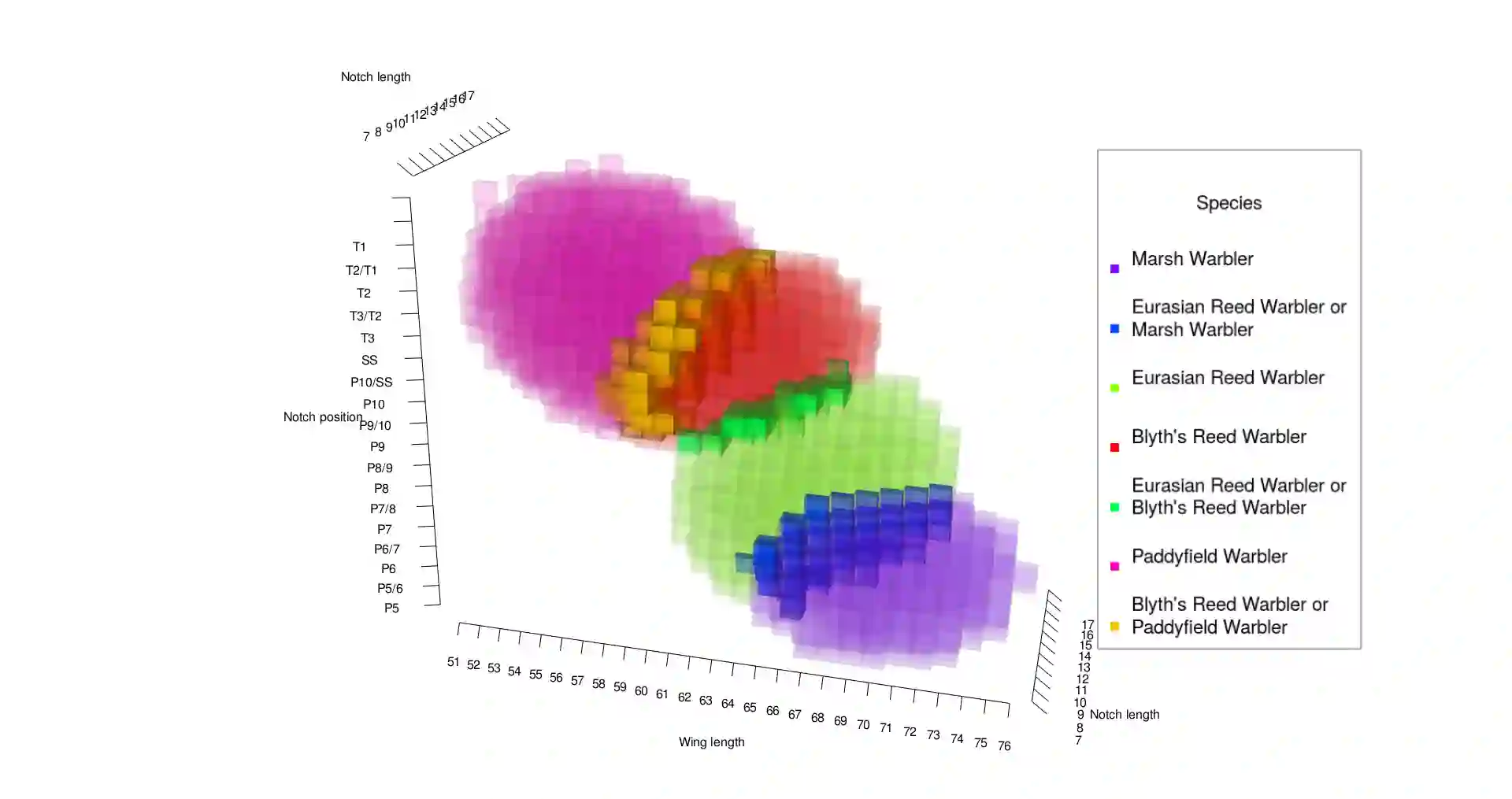
Identification of taxa can significantly be assisted by statistical classification based on trait measurements in two major ways; either individually or by phylogenetic (clustering) methods. In this paper we present a general Bayesian approach for classifying species individually based on measurements of a mixture of continuous and ordinal traits as well as any type of covariates. It is assumed that the trait vector is derived from a latent variable with a multivariate Gaussian distribution. Decision rules based on supervised learning are presented that estimate model parameters through blockwise Gibbs sampling. These decision regions allow for uncertainty (partial rejection), so that not necessarily one specific category (taxon) is output when new subjects are classified, but rather a set of categories including the most probable taxa. This type of discriminant analysis employs reward functions with a set-valued input argument, so that an optimal Bayes classifier can be defined. We also present a way of safeguarding against outlying new observations, using an analogue of a $p$-value within our Bayesian setting. Our method is illustrated on an original ornithological data set of birds. We also incorporate model selection through cross-validation, examplified on another original data set of birds.
翻译:基于特征测量的统计分类可以大大地协助分类的确定,这种分类主要有两种方式:个别的或植物遗传(集群)方法。在本文中,我们提出一种一般的巴伊西亚方法,根据连续和正态特性以及任何类型的共变体的混合测量对物种进行个别分类;假定特性矢量来自具有多变量分布的隐性变量;基于监督学习的决定规则通过块状Gibs抽样来估计模型参数。这些决策区域允许不确定性(部分拒绝),因此在新科目分类时不一定有一个特定类别(税)是产出,而是一组类别,包括最有可能的分类。这种差异性分析采用有定值的投入论证的奖励功能,从而可以界定最佳的海湾分类器。我们还提出一种办法,防止利用贝伊西亚环境内的美元价值的类比值来进行新观测。我们的方法是用原始或氮学的鸟类数据集来说明。我们还采用了另一种经过交叉对比测试的原始鸟类模型选择。