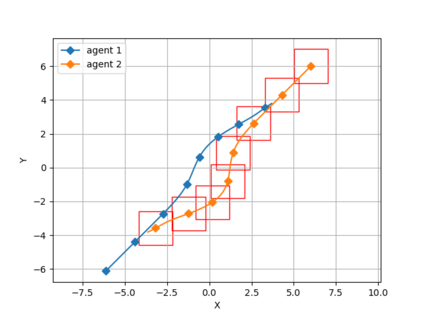
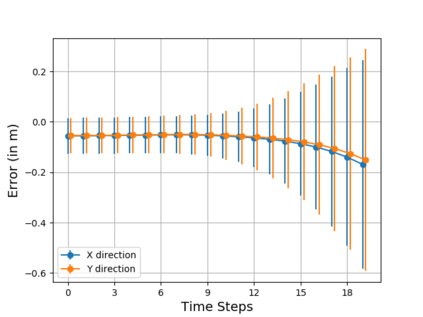
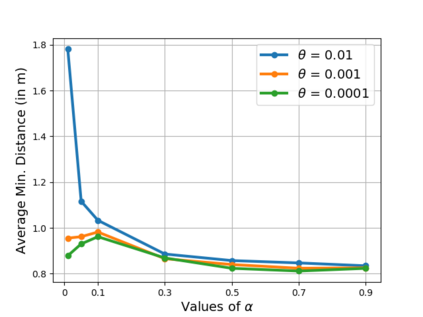
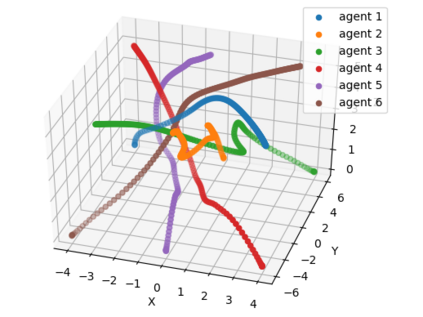
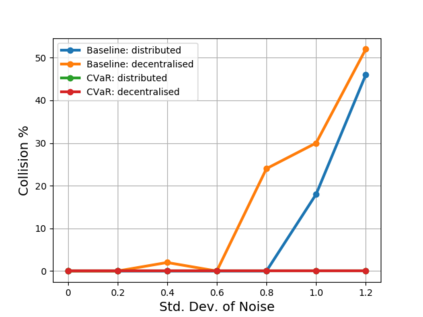
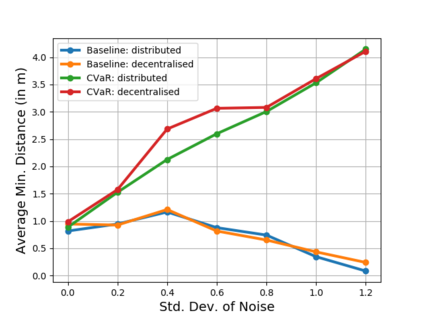
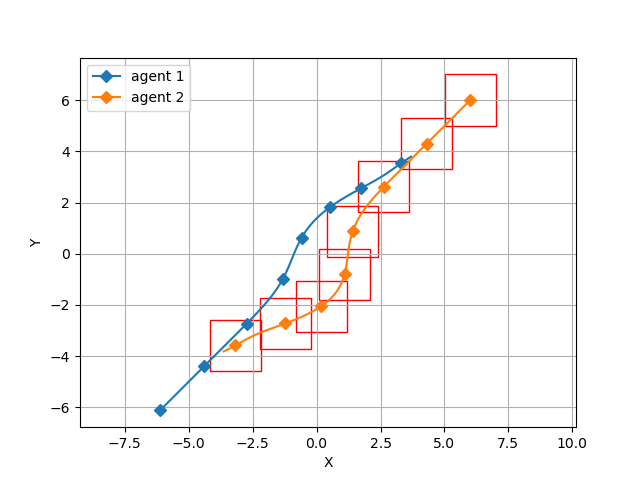
Safe navigation is a fundamental challenge in multi-robot systems due to the uncertainty surrounding the future trajectory of the robots that act as obstacles for each other. In this work, we propose a principled data-driven approach where each robot repeatedly solves a finite horizon optimization problem subject to collision avoidance constraints with latter being formulated as distributionally robust conditional value-at-risk (CVaR) of the distance between the agent and a polyhedral obstacle geometry. Specifically, the CVaR constraints are required to hold for all distributions that are close to the empirical distribution constructed from observed samples of prediction error collected during execution. The generality of the approach allows us to robustify against prediction errors that arise under commonly imposed assumptions in both distributed and decentralized settings. We derive tractable finite-dimensional approximations of this class of constraints by leveraging convex and minmax duality results for Wasserstein distributionally robust optimization problems. The effectiveness of the proposed approach is illustrated in a multi-drone navigation setting implemented in Gazebo platform.
翻译:安全导航是多机器人系统面临的一个根本挑战,因为机器人未来轨道的不确定性是相互构成障碍的。在这项工作中,我们提议采用有原则的数据驱动方法,即每个机器人反复解决受避免碰撞限制的有限地平优化问题,后者被拟订为具有分布性强的有条件风险值(CVaR),其介质和多面性障碍的几何法,具体地说,CVaR的制约要求维持与执行期间所收集的观测预测错误样品所得出的实证分布相近的所有分布。这种方法的笼统性使我们能够抵御在分布式和分散式环境中共同设定的假设中产生的预测错误。我们通过利用电磁盘和微量性二元效应,为瓦塞尔斯坦分布性强的优化问题取得可控的制约。在加泽博平台上实施的多轨道导航设置中说明了拟议方法的有效性。