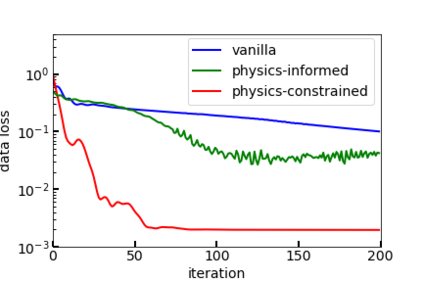
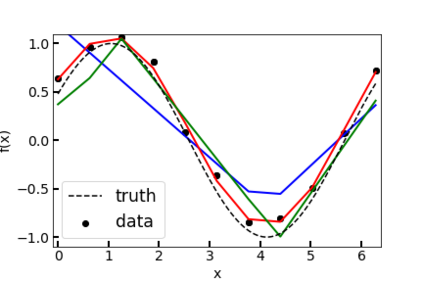
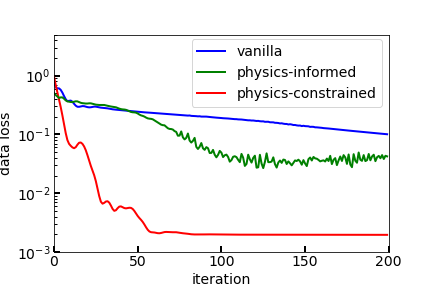
We illustrate an approach that can be exploited for constructing neural networks which a priori obey physical laws. We start with a simple single-layer neural network (NN) but refrain from choosing the activation functions yet. Under certain conditions and in the infinite-width limit, we may apply the central limit theorem, upon which the NN output becomes Gaussian. We may then investigate and manipulate the limit network by falling back on Gaussian process (GP) theory. It is observed that linear operators acting upon a GP again yield a GP. This also holds true for differential operators defining differential equations and describing physical laws. If we demand the GP, or equivalently the limit network, to obey the physical law, then this yields an equation for the covariance function or kernel of the GP, whose solution equivalently constrains the model to obey the physical law. The central limit theorem then suggests that NNs can be constructed to obey a physical law by choosing the activation functions such that they match a particular kernel in the infinite-width limit. The activation functions constructed in this way guarantee the NN to a priori obey the physics, up to the approximation error of non-infinite network width. Simple examples of the homogeneous 1D-Helmholtz equation are discussed and compared to naive kernels and activations.
翻译:我们展示了一种可用于建设神经网络的方法,这些神经网络可以先天地服从物理法则。 我们从简单的单层神经网络开始, 但没有选择激活功能。 在某些条件下, 在无限宽限的限制下, 我们可以应用核心限制定理, 即NN输出成为高斯文。 然后我们可以通过返回高西亚进程理论来调查和操控限制网络。 人们发现, 在 GP 上运行的线性操作员再次产生一个 GP。 对于定义差异方程式和描述物理法则的不同操作员来说, 这一点也是真实的。 如果我们要求GP, 或相当于限制网络, 来遵守物理法则在某些条件下和无限宽限的限度内, 那么我们就可以应用中央限定律来测量和操控限制网络。 中央限后显示, 线性操作者可以通过选择与无限宽限内某个特定的内核功能相匹配的激活功能来构建。 如果我们要求GPO, 或者说, 等量网络的等量功能, 将产生一个等同的等同的等式等同的公式。 这样构建的激活功能将保证GNN和S- 比较的系统之前的深度, 的深度将模拟模拟模拟的模拟模拟的模拟的模拟的模拟的模拟的模拟和模拟的模拟, 。