Collective Proposal Distributions for Nonlinear MCMC samplers: Mean-Field Theory and Fast Implementation

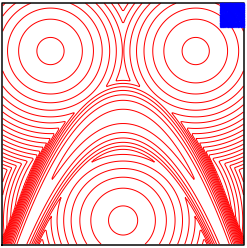
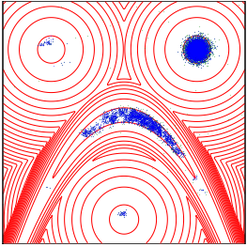
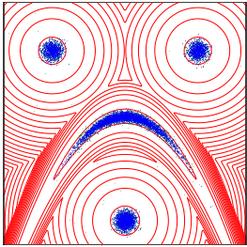
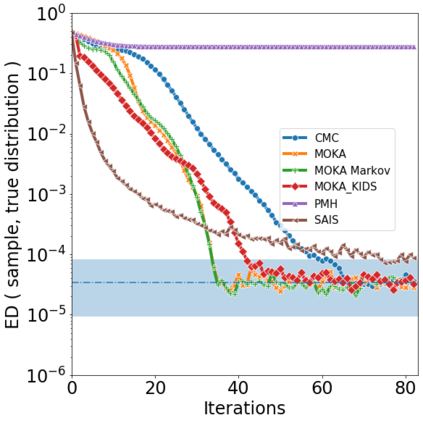
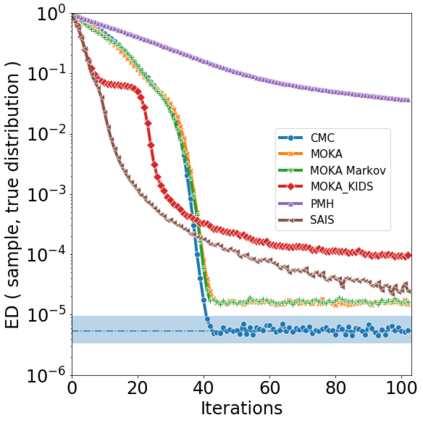
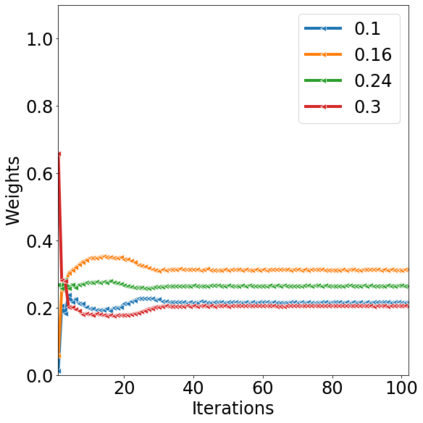
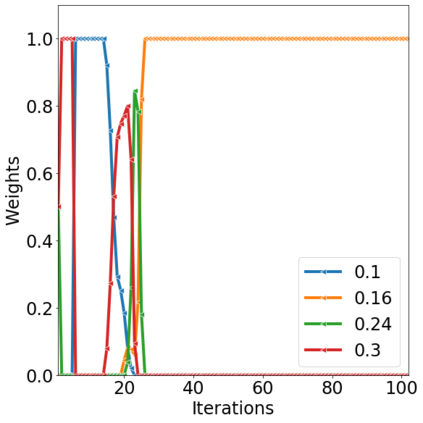
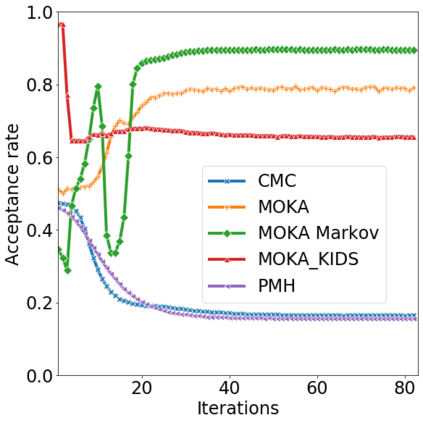
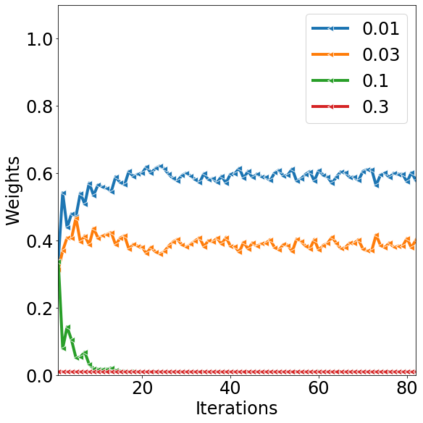
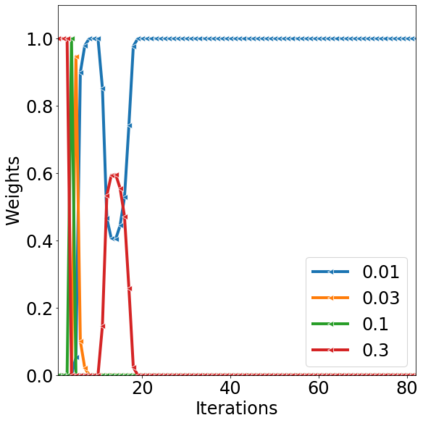
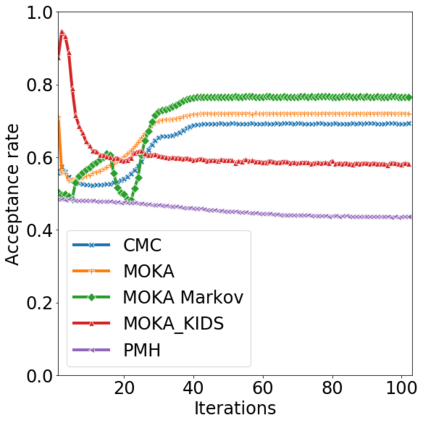
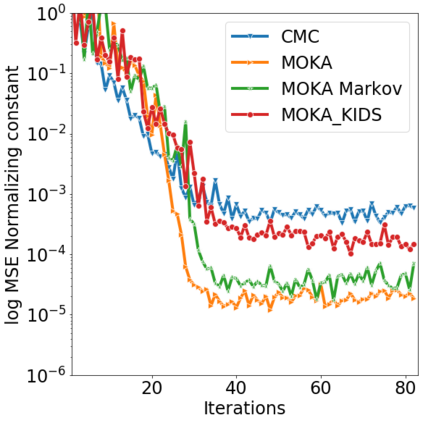
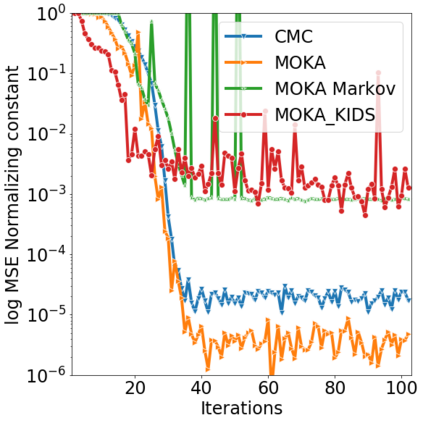
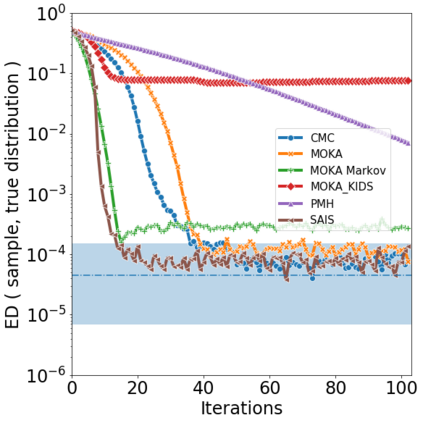
Over the last decades, various "non-linear" MCMC methods have arisen. While appealing for their convergence speed and efficiency, their practical implementation and theoretical study remain challenging. In this paper, we introduce a non-linear generalization of the Metropolis-Hastings algorithm to a proposal that depends not only on the current state, but also on its law. We propose to simulate this dynamics as the mean field limit of a system of interacting particles, that can in turn itself be understood as a generalisation of the Metropolis-Hastings algorithm to a population of particles. We prove the convergence of this algorithm under the double limit in number of iterations and number of particles. Then, we propose an efficient GPU implementation and illustrate its performance on various examples.