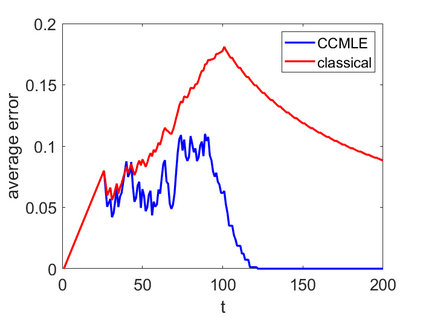
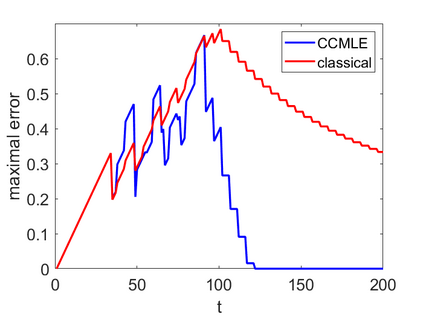
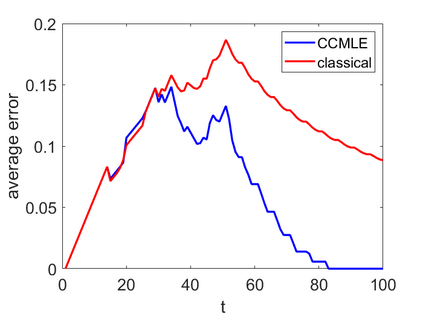
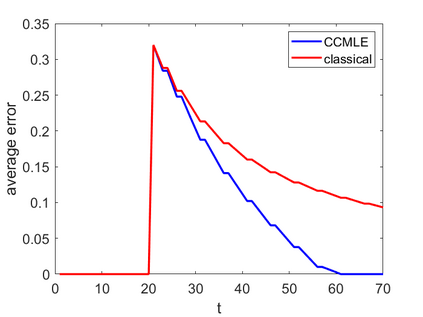
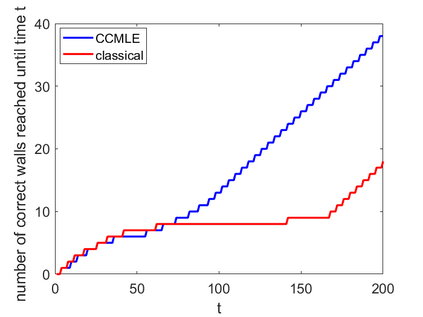
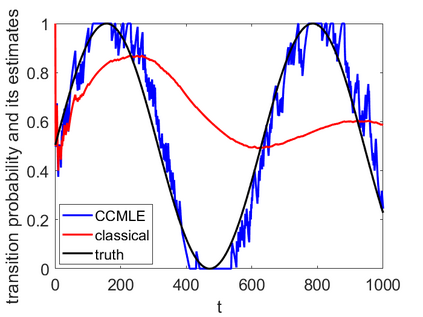
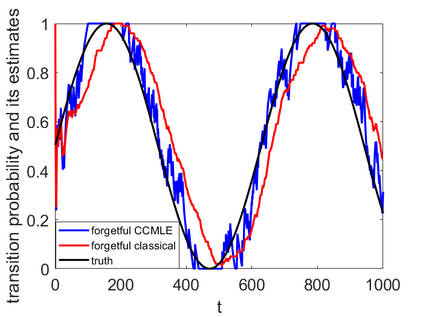
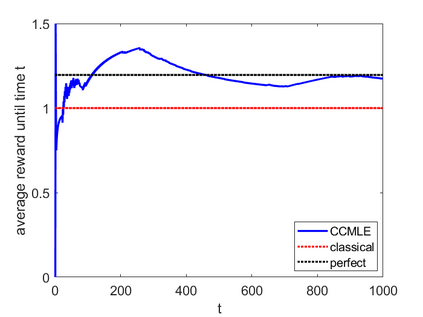
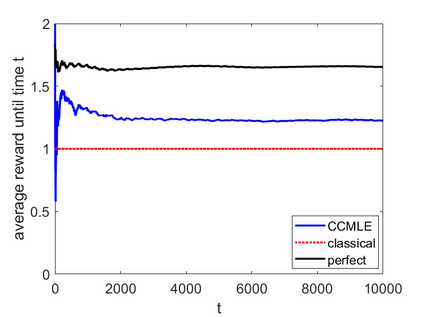
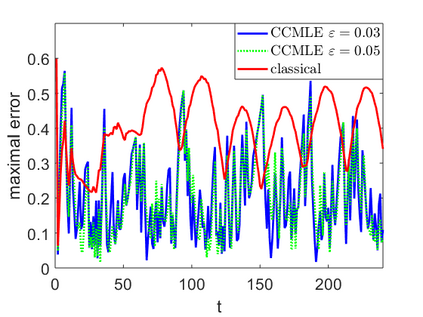
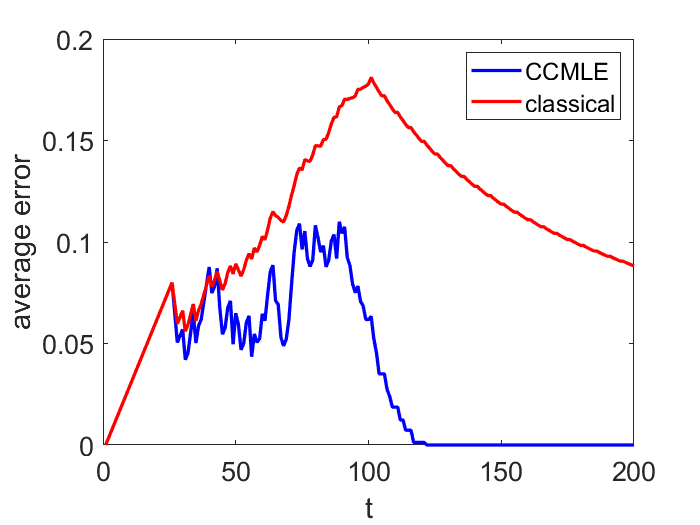
This paper proposes a formal approach to online learning and planning for agents operating in a priori unknown, time-varying environments. The proposed method computes the maximally likely model of the environment, given the observations about the environment made by an agent earlier in the system run and assuming knowledge of a bound on the maximal rate of change of system dynamics. Such an approach generalizes the estimation method commonly used in learning algorithms for unknown Markov decision processes with time-invariant transition probabilities, but is also able to quickly and correctly identify the system dynamics following a change. Based on the proposed method, we generalize the exploration bonuses used in learning for time-invariant Markov decision processes by introducing a notion of uncertainty in a learned time-varying model, and develop a control policy for time-varying Markov decision processes based on the exploitation and exploration trade-off. We demonstrate the proposed methods on four numerical examples: a patrolling task with a change in system dynamics, a two-state MDP with periodically changing outcomes of actions, a wind flow estimation task, and a multi-armed bandit problem with periodically changing probabilities of different rewards.
翻译:本文建议了一种正式的在线学习和规划方法,用于在先天未知、时间变化的环境中运作的代理商。考虑到系统运行早期一个代理商对环境的观察,并假定对系统动态最大变化率的界限的了解,拟议方法计算了最可能的环境模型。这种方法概括了在未知的Markov决策过程学习算法中常用的估计方法,具有时间变化性过渡概率,但也能够迅速和正确地确定系统变化后的动态。根据拟议方法,我们推广用于学习时间变化性马尔科夫决策过程的勘探奖金,在学习时间变化性马尔科夫决策过程中引入一种不确定性的概念,并根据开发和探索交易,为时间变化的马尔科夫决策过程制定一项控制政策。我们用四个数字实例展示了拟议方法:巡逻任务,系统动态变化,两州MDP,行动结果定期变化,风流估计任务,以及多臂强、不同奖励概率变化不时变化的问题。