Quickest Change Detection with Non-stationary and Composite Post-change Distribution

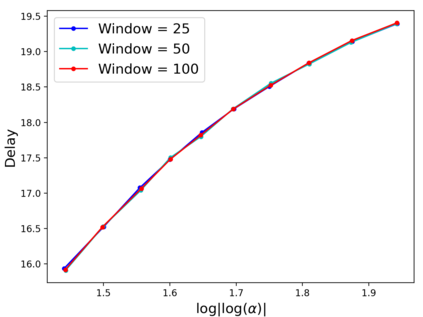
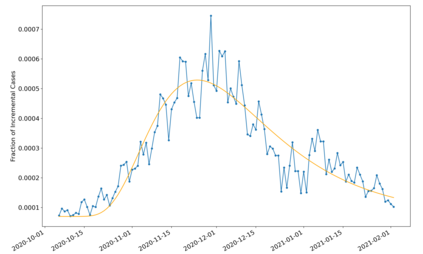
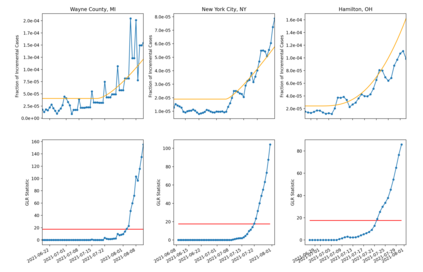
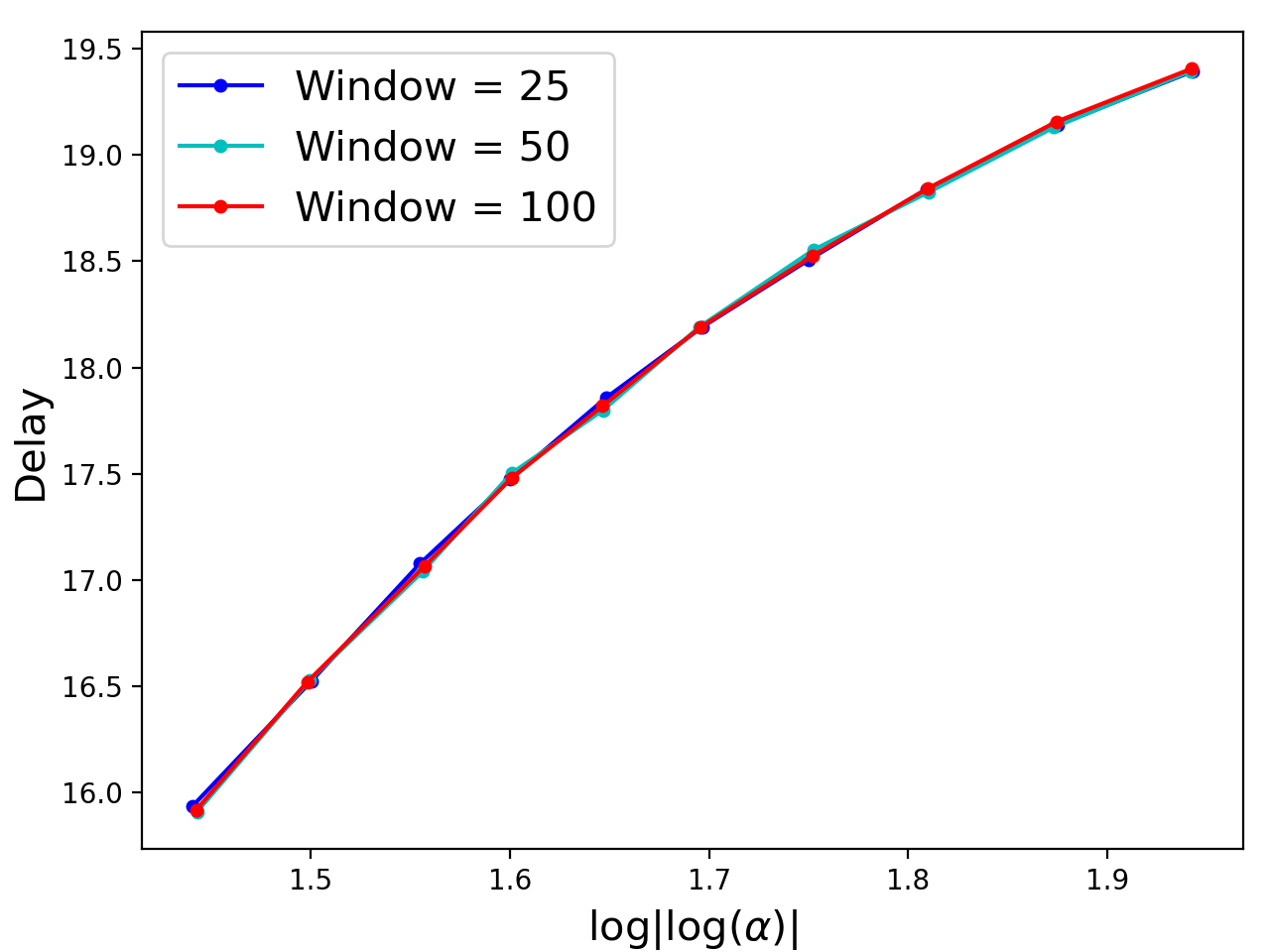
The problem of quickest detection of a change in the distribution of a sequence of independent observations is considered. The pre-change distribution is assumed to be known and stationary, while the post-change distributions are assumed to evolve in a pre-determined non-stationary manner with some possible parametric uncertainty. In particular, it is assumed that the cumulative KL divergence between the post-change and the pre-change distributions grows super-linearly with time after the change-point. For the case where the post-change distributions are known, a universal asymptotic lower bound on the delay is derived, as the false alarm rate goes to zero. Furthermore, a window-limited CuSum test is developed, and shown to achieve the lower bound asymptotically. For the case where the post-change distributions have parametric uncertainty, a window-limited generalized likelihood-ratio test is developed and is shown to achieve the universal lower bound asymptotically. Extensions to the case with dependent observations are discussed. The analysis is validated through numerical results on synthetic data. The use of the window-limited generalized likelihood-ratio test in monitoring pandemics is also demonstrated.