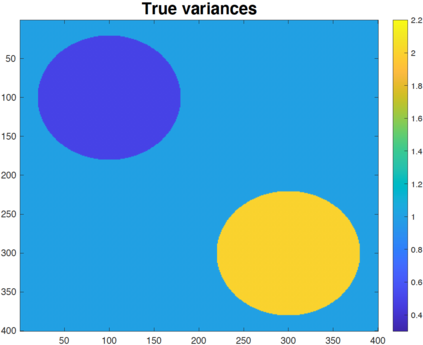
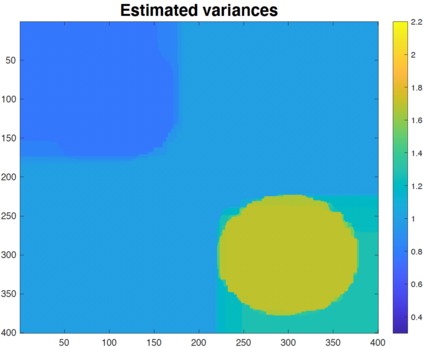
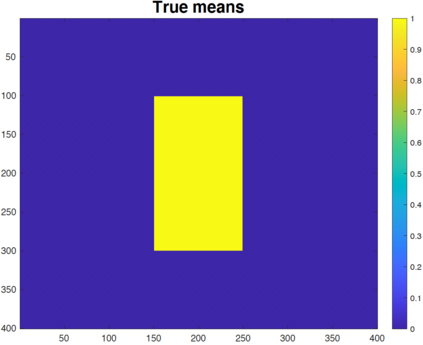
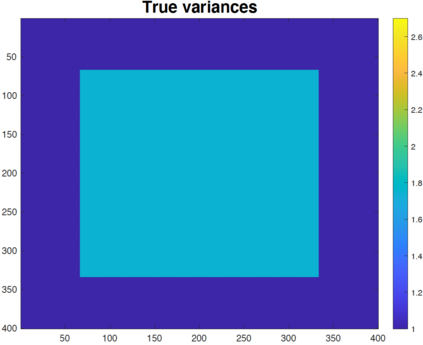
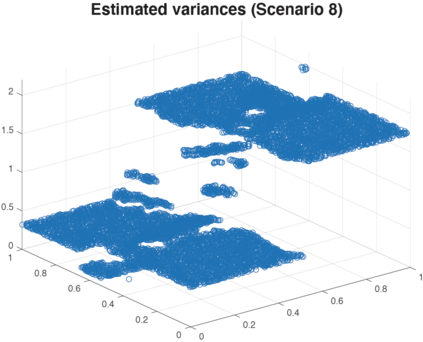
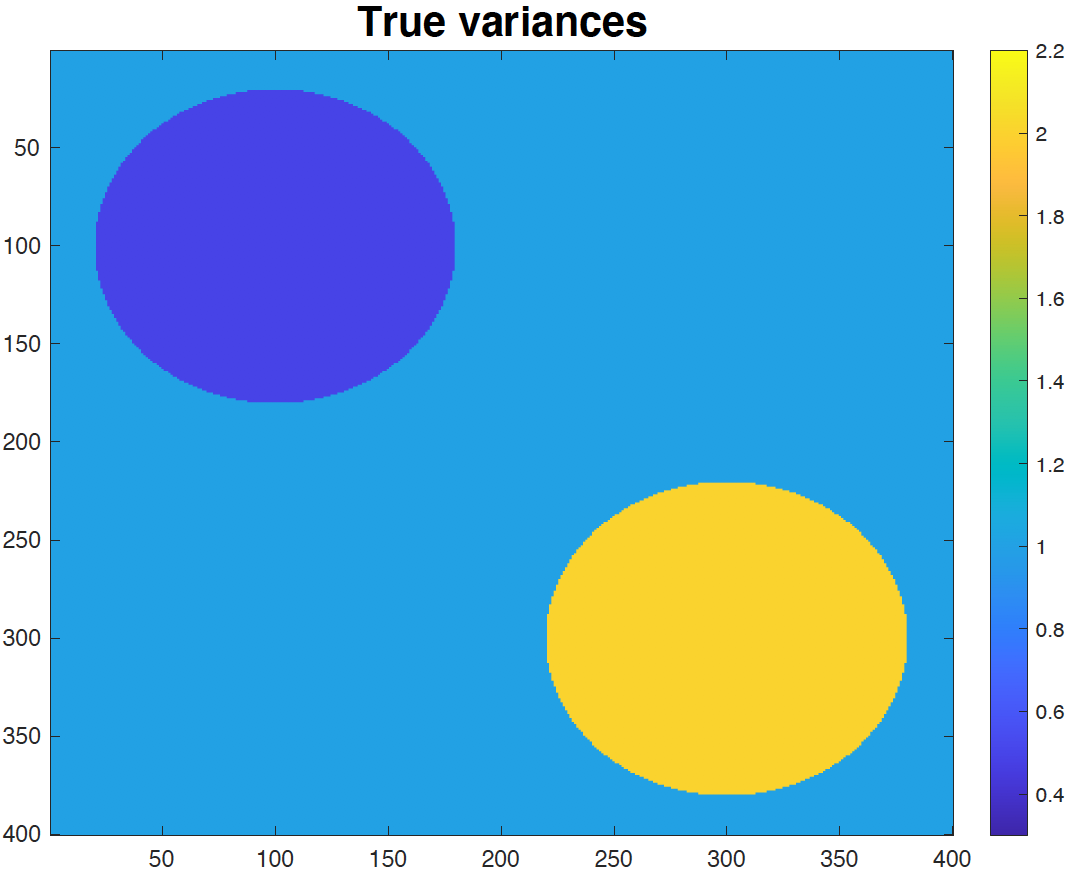
We study the problem of variance estimation in general graph-structured problems. First, we develop a linear time estimator for the homoscedastic case that can consistently estimate the variance in general graphs. We show that our estimator attains minimax rates for the chain and 2D grid graphs when the mean signal has a total variation with canonical scaling. Furthermore, we provide general upper bounds on the mean squared error performance of the fused lasso estimator in general graphs under a moment condition and a bound on the tail behavior of the errors. These upper bounds allow us to generalize for broader classes of distributions, such as sub-Exponential, many existing results on the fused lasso that are only known to hold with the assumption that errors are sub-Gaussian random variables. Exploiting our upper bounds, we then study a simple total variation regularization estimator for estimating the signal of variances in the heteroscedastic case. Our results show that the variance estimator attains minimax rates for estimating signals of bounded variation in grid graphs, $K$-nearest neighbor graphs with very mild assumptions, and it is consistent for estimating the variances in any connected graph. In addition, extensive numerical results show that our proposed estimators perform reasonably well in a variety of graph-structured models.
翻译:我们用一般图形结构问题来研究差异估计问题。 首先, 我们为同质偏差案例开发一个线性时间测算器, 可以持续估计一般图形的差异。 我们显示, 当平均信号与罐体缩放有完全差异时, 我们的测算器达到链和 2D 网格图的最小值率和 2D 网格图。 此外, 我们提供一般图形中连接的 lasso 估测器的平均正方差值的上限值, 在一个时段条件下, 并且 锁定错误的尾端行为 。 这些上限允许我们为分布范围更广的分布类别( 如亚扩展值) 进行概括。 我们显示, 我们的测算器在连接的 线条线上有许多现有结果, 只能与误差是 亚裔随机随机变数的假设。 探索我们的上限, 我们然后研究一个简单的全方位变校正校正校正的测算仪, 我们的估测算器在图表中达到了微缩缩缩率率率率率, 显示, 模型显示, 图表中显示, 度变化的缩度变化的缩图显示, 显示, 显示, 度变化的模型显示, 度变化的模型显示, 度变化的缩缩缩的图像中的任何 显示, 。